7  第10章 セグメントとクラスター分析

クラスター分析(cluster analysis)は、観測値をいくつかのグループに分ける手法です。ここでは、階層的クラスター分析と非階層的クラスター分析(K-means法)を学習します。

7.1 階層的クラスター分析

データの中から類似している観測値を段階的にクラスターとしてまとめて、最終的に1つのクラスターになるまで繰り返す方法です。 類似度は距離で測定され、距離が近いほど類似しているとみなされます。 距離概念として、

  • ユークリッド距離(Euclidean distance)
  • マンハッタン距離(Manhattan distance)
  • マハラノビス距離(Mahalanobis distance)

などがあります。 デンドログラム(dendrogram)という樹形図を使って、クラスターの結合過程を視覚的に表現します。

2023年実施の消費者調査アンケートデータを使って、階層的クラスター分析を実行してみます。 必要なパッケージを読み込みます。

  • tidyverse: データ操作と可視化
  • readxl: Excelデータの読み込み
  • cluster: クラスター分析
  • factoextra: クラスター分析の可視化
  • ggrepel: グラフ上のラベル配置
  • useful: 便利な関数群

そしてデータを読み込みます。 read_xlsx()関数の引数として，

  • path: データファイルのパスとファイル名
  • sheet: 読み込むシート名
  • na: 欠損値を表す文字列
pacman::p_load(tidyverse, readxl, cluster, factoextra, ggrepel, useful)
# コード10-1
df_cons <- read_xlsx(
  path = "data/回答データ【消費者調査2023年度下期調査】.xlsx",
  sheet = "回答データ【共通調査2023年度下期】",
  na = " "
  )

読み込んだデータをstr()で確認します。

df_cons |>str()
tibble [5,364 × 992] (S3: tbl_df/tbl/data.frame)
 $ 2023年下期no: num [1:5364] 1 2 3 4 7 8 9 10 11 12 ...
 $ 県番号      : num [1:5364] 13 13 27 14 13 13 14 11 25 14 ...
 $ 地域分類    : num [1:5364] 3 3 6 3 3 3 3 3 6 3 ...
 $ 性別        : num [1:5364] 2 1 1 1 1 1 2 2 1 2 ...
 $ 年齢        : num [1:5364] 38 42 25 26 30 33 52 53 36 26 ...
 $ 年齢階層    : num [1:5364] 3 4 2 2 3 3 5 5 3 2 ...
 $ 性年代      : num [1:5364] 11 4 2 2 3 3 13 13 3 10 ...
 $ 結婚有無    : num [1:5364] 2 2 1 1 1 1 1 2 1 2 ...
 $ q1          : num [1:5364] 2 1 1 1 1 1 2 2 1 2 ...
 $ q2t         : num [1:5364] 38 42 25 26 30 33 52 53 36 26 ...
 $ q3          : num [1:5364] 13 13 27 14 13 13 14 11 25 14 ...
 $ q4          : num [1:5364] 1 1 2 2 2 2 2 1 2 1 ...
 $ q5          : num [1:5364] 8 2 7 3 3 3 3 8 4 4 ...
 $ q6          : num [1:5364] 2 2 3 4 1 1 1 2 1 2 ...
 $ q7_1        : num [1:5364] 1 8 2 10 3 5 6 1 5 5 ...
 $ q7_2        : num [1:5364] 4 9 3 10 NA NA NA 4 NA 8 ...
 $ q8          : num [1:5364] 4 4 2 5 2 2 4 1 4 4 ...
 $ q9          : num [1:5364] 1 4 1 2 2 4 1 5 6 5 ...
 $ q10         : num [1:5364] 4 7 2 7 1 1 3 5 NA 5 ...
 $ q11_1       : num [1:5364] 5 4 1 3 4 2 4 2 3 2 ...
 $ q11_2       : num [1:5364] 4 5 2 3 4 2 3 2 3 2 ...
 $ q11_3       : num [1:5364] 4 5 2 3 3 2 4 2 3 2 ...
 $ q11_4       : num [1:5364] 4 4 3 3 4 2 4 2 3 2 ...
 $ q11_5       : num [1:5364] 4 4 3 4 4 2 4 2 3 2 ...
 $ q11_6       : num [1:5364] 4 4 3 3 3 2 4 2 3 2 ...
 $ q11_7       : num [1:5364] 4 5 2 3 4 1 4 2 3 2 ...
 $ q11_8       : num [1:5364] 4 4 3 3 4 1 3 2 3 2 ...
 $ q11_9       : num [1:5364] 4 4 3 2 4 2 5 2 3 3 ...
 $ q11_10      : num [1:5364] 4 5 4 3 3 2 3 2 3 3 ...
 $ q11_11      : num [1:5364] 4 5 3 3 4 2 4 2 3 2 ...
 $ q11_12      : num [1:5364] 4 4 3 3 3 1 4 2 3 2 ...
 $ q11_13      : num [1:5364] 4 4 2 3 3 1 3 3 3 2 ...
 $ q11_14      : num [1:5364] 4 4 2 3 4 1 4 4 3 2 ...
 $ q11_15      : num [1:5364] 4 4 3 4 4 2 3 4 3 2 ...
 $ q11_16      : num [1:5364] 4 4 3 3 4 2 5 3 3 2 ...
 $ q11_17      : num [1:5364] 4 5 3 3 5 2 4 3 3 2 ...
 $ q11_18      : num [1:5364] 4 4 2 3 4 2 4 3 3 3 ...
 $ q11_19      : num [1:5364] 4 5 2 3 5 2 5 3 3 4 ...
 $ q11_20      : num [1:5364] 4 4 3 3 4 2 4 3 3 2 ...
 $ q11_21      : num [1:5364] 4 4 3 3 5 2 3 3 3 4 ...
 $ q11_22      : num [1:5364] 4 4 3 3 4 2 3 3 3 3 ...
 $ q11_23      : num [1:5364] 4 4 4 3 4 1 5 3 3 2 ...
 $ q11_24      : num [1:5364] 4 5 3 3 5 1 4 3 3 2 ...
 $ q11_25      : num [1:5364] 4 4 3 4 4 1 4 3 3 2 ...
 $ q12_1       : num [1:5364] 2 2 3 4 1 3 3 2 3 2 ...
 $ q12_2       : num [1:5364] 2 1 4 3 2 3 2 5 3 4 ...
 $ q12_3       : num [1:5364] 2 2 3 3 1 4 2 5 3 4 ...
 $ q12_4       : num [1:5364] 2 2 3 3 1 4 2 5 3 4 ...
 $ q12_5       : num [1:5364] 2 1 4 3 2 5 3 5 3 4 ...
 $ q13_1       : num [1:5364] 2 2 3 4 2 4 2 2 2 2 ...
 $ q13_2       : num [1:5364] 2 2 3 3 2 5 2 2 2 3 ...
 $ q13_3       : num [1:5364] 2 1 3 3 2 5 2 3 2 2 ...
 $ q13_4       : num [1:5364] 4 5 3 3 5 1 3 3 1 2 ...
 $ q14_1       : num [1:5364] 4 3 3 3 3 2 2 4 3 2 ...
 $ q14_2       : num [1:5364] 4 4 3 3 3 2 2 4 3 3 ...
 $ q14_3       : num [1:5364] 4 4 3 3 3 1 2 4 3 4 ...
 $ q14_4       : num [1:5364] 4 4 3 3 2 1 4 4 3 3 ...
 $ q14_5       : num [1:5364] 4 4 3 3 3 2 5 4 3 3 ...
 $ q14_6       : num [1:5364] 4 5 2 2 3 2 4 4 4 4 ...
 $ q14_7       : num [1:5364] 4 4 3 3 4 2 2 3 3 3 ...
 $ q14_8       : num [1:5364] 4 5 3 4 3 2 2 3 3 3 ...
 $ q14_9       : num [1:5364] 4 4 3 3 5 2 3 3 3 4 ...
 $ q14_10      : num [1:5364] 4 5 2 3 5 1 4 3 3 4 ...
 $ q14_11      : num [1:5364] 4 5 3 3 4 1 2 3 4 2 ...
 $ q14_12      : num [1:5364] 4 4 3 3 3 1 4 3 3 3 ...
 $ q14_13      : num [1:5364] 4 4 3 3 4 2 4 3 3 4 ...
 $ q14_14      : num [1:5364] 4 4 3 3 3 2 2 3 3 3 ...
 $ q14_15      : num [1:5364] 4 5 3 3 3 2 4 3 4 3 ...
 $ q14_16      : num [1:5364] 4 5 2 3 4 1 2 3 3 3 ...
 $ q14_17      : num [1:5364] 4 5 2 3 4 1 4 4 4 3 ...
 $ q15_1       : num [1:5364] 1 2 3 3 2 4 3 3 3 2 ...
 $ q15_2       : num [1:5364] 2 2 3 3 3 5 2 3 3 4 ...
 $ q15_3       : num [1:5364] 2 2 3 3 2 5 2 3 3 3 ...
 $ q15_4       : num [1:5364] 2 1 3 2 3 5 2 3 3 2 ...
 $ q15_5       : num [1:5364] 2 2 3 3 3 4 3 3 3 2 ...
 $ q15_6       : num [1:5364] 2 2 3 2 2 4 1 3 2 3 ...
 $ q15_7       : num [1:5364] 2 2 5 2 3 4 2 3 3 3 ...
 $ q16_1       : num [1:5364] 2 1 3 4 3 3 3 2 4 2 ...
 $ q16_2       : num [1:5364] 2 2 3 3 3 4 4 3 4 2 ...
 $ q16_3       : num [1:5364] 2 2 3 3 3 4 2 3 3 3 ...
 $ q16_4       : num [1:5364] 2 2 3 3 3 4 3 3 3 3 ...
 $ q17_1.01    : num [1:5364] 0 1 0 0 1 1 0 0 0 1 ...
 $ q17_1.02    : num [1:5364] 0 1 0 0 0 0 0 0 0 0 ...
 $ q17_1.03    : num [1:5364] 0 0 0 0 0 0 0 0 0 1 ...
 $ q17_1.04    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.05    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.06    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.07    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.08    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.09    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.10    : num [1:5364] 0 0 0 0 1 0 0 0 0 0 ...
 $ q17_1.11    : num [1:5364] 0 0 0 0 0 0 0 1 0 0 ...
 $ q17_1.12    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.13    : num [1:5364] 0 0 0 0 1 0 0 1 0 0 ...
 $ q17_1.14    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.15    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.16    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
 $ q17_1.17    : num [1:5364] 0 1 0 0 1 0 0 0 0 0 ...
 $ q17_1.18    : num [1:5364] 0 0 0 0 0 0 0 0 0 0 ...
  [list output truncated]

992変数，5364観測値からなるデータを読み込みました。 東京都(13)と兵庫県(28)の回答者を対象に，ブランド志向性(q12_4)と価格志向性(q13_3)の2変数を使ってクラスター分析を実行します。

教科書では，カテゴリー変数の数値を文字列に変換するために，case_when()関数を使っていますが， この処理だと変数の型が文字列となり，カテゴリー変数としてRが認識しなくなります。 そこでここでは，factor()関数を使って，変数の型を因子型に変換し，ラベルを付与する方法を採用します。

# 東京と兵庫の県番号リスト作成
ken_number   <- c(13, 28)
# 因子型のラベル作成
pref_labels  <- c("Tokyo", "Hyogo")
gender_label <- c("Male", "Female")
marital_label <- c("Married", "Not Married")

# 回答者と項目を抽出
df_cons <- df_cons |>
  select(県番号, 性別, 年齢, 結婚有無, q12_4, q13_3) |>
  filter(
    県番号 %in% ken_number, # 東京と兵庫の回答者
    q12_4 != 999,           # 欠損値は999
    q13_3 != 999
  ) |>
  mutate(
    q12_4 = 6 - q12_4, # 尺度を反転
    q13_3 = 6 - q13_3, # 尺度を反転
    Pref       = factor(県番号,  levels  = ken_number, labels = pref_labels),
    Gender     = factor(性別,    levels  = c(1, 2), labels = gender_label),
    MaritalSt. = factor(結婚有無, levels = c(1, 2), labels = marital_label)
  )

クラスター分析を実行する関数の引数は数値データのみである必要があるので，select()で必要な変数だけを抽出し，オブジェクトclus_consに格納します。

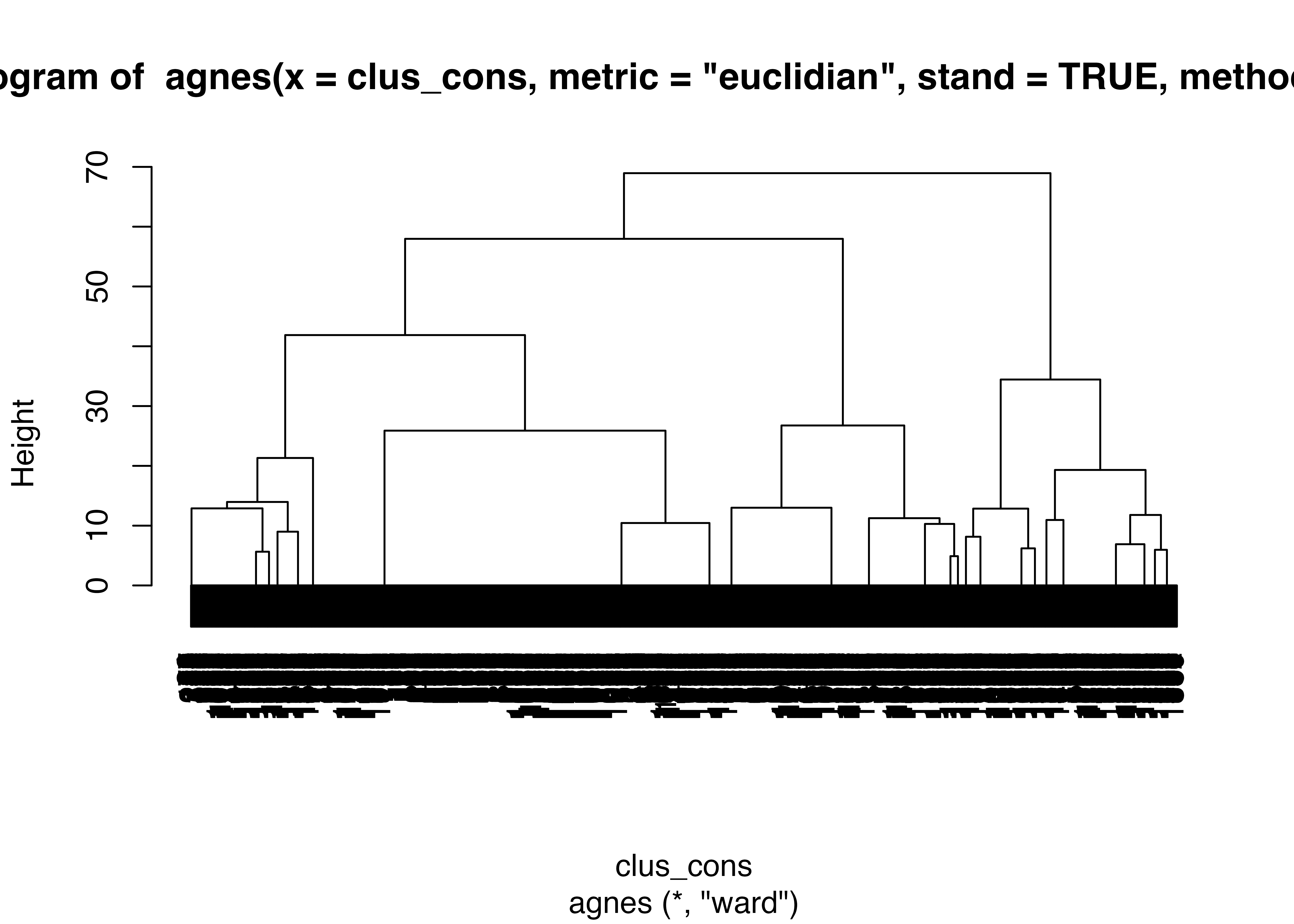
agnes()関数を使って階層的クラスター分析を実行します。引数として，

  • clus_cons: クラスター分析対象データ
  • metric: 距離尺度
  • method: クラスター結合方法
  • stand: 変数の標準化

を指定します。 実行結果をHier1に格納し，pltree()関数でデンドログラムを作成します。

clus_cons <- df_cons |> select(q12_4, q13_3)


Hier1 <- agnes(
  clus_cons, # クラスター分析対象データ
  metric = "euclidian", # 距離尺度
  method = "ward", # クラスター結合方法
  stand = TRUE # 変数の標準化
  )

pltree(Hier1) # デンドログラムの作成

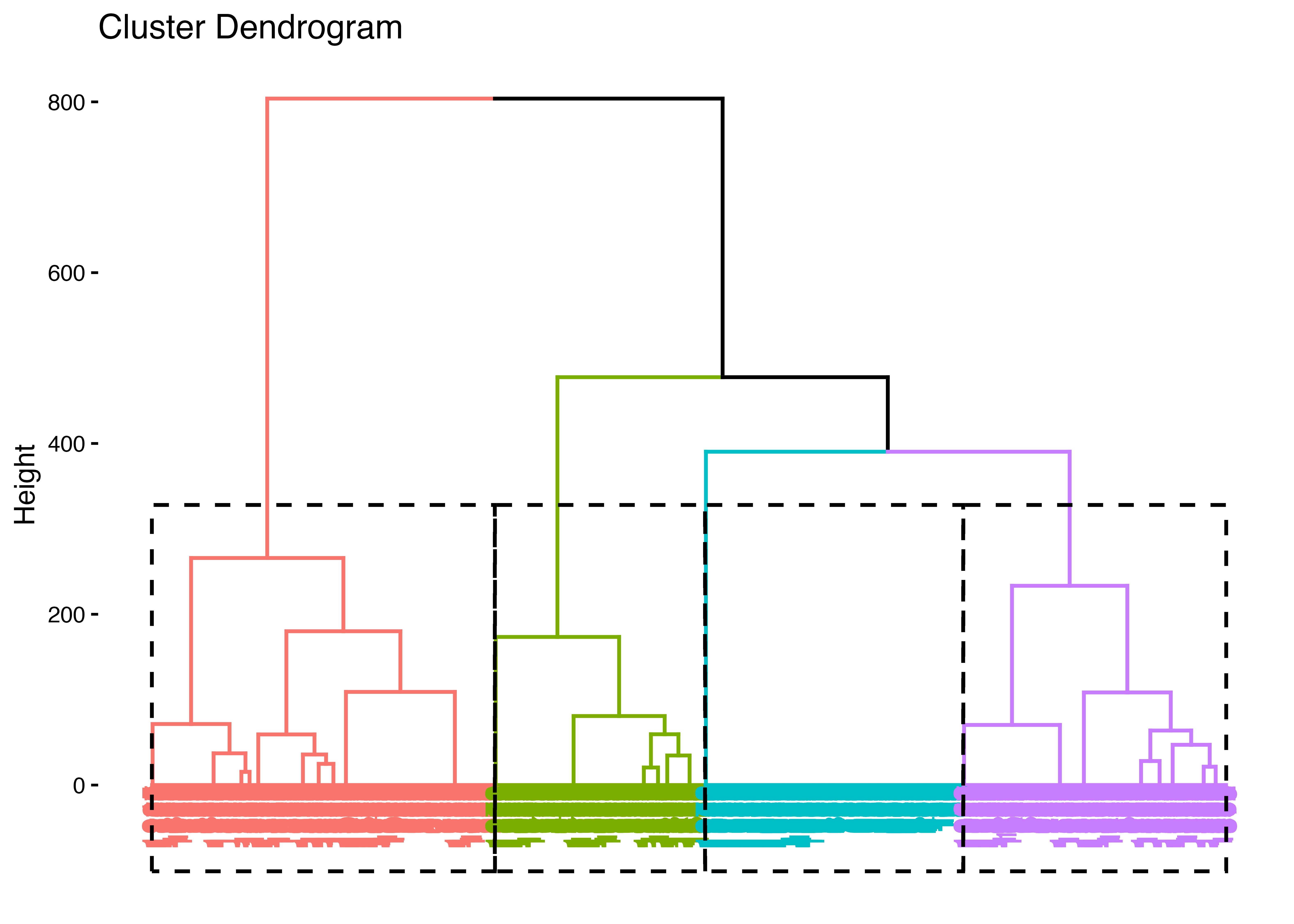
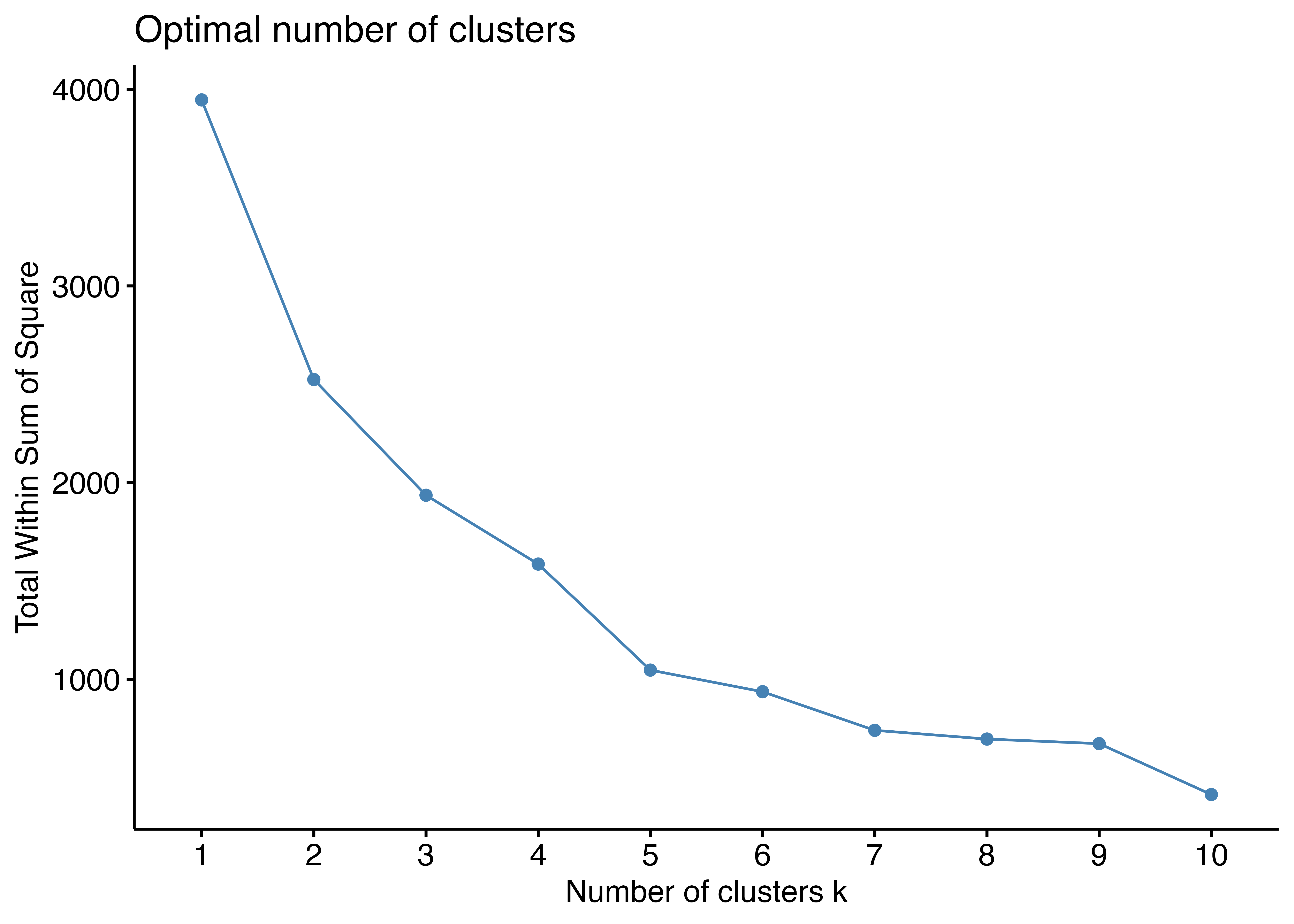
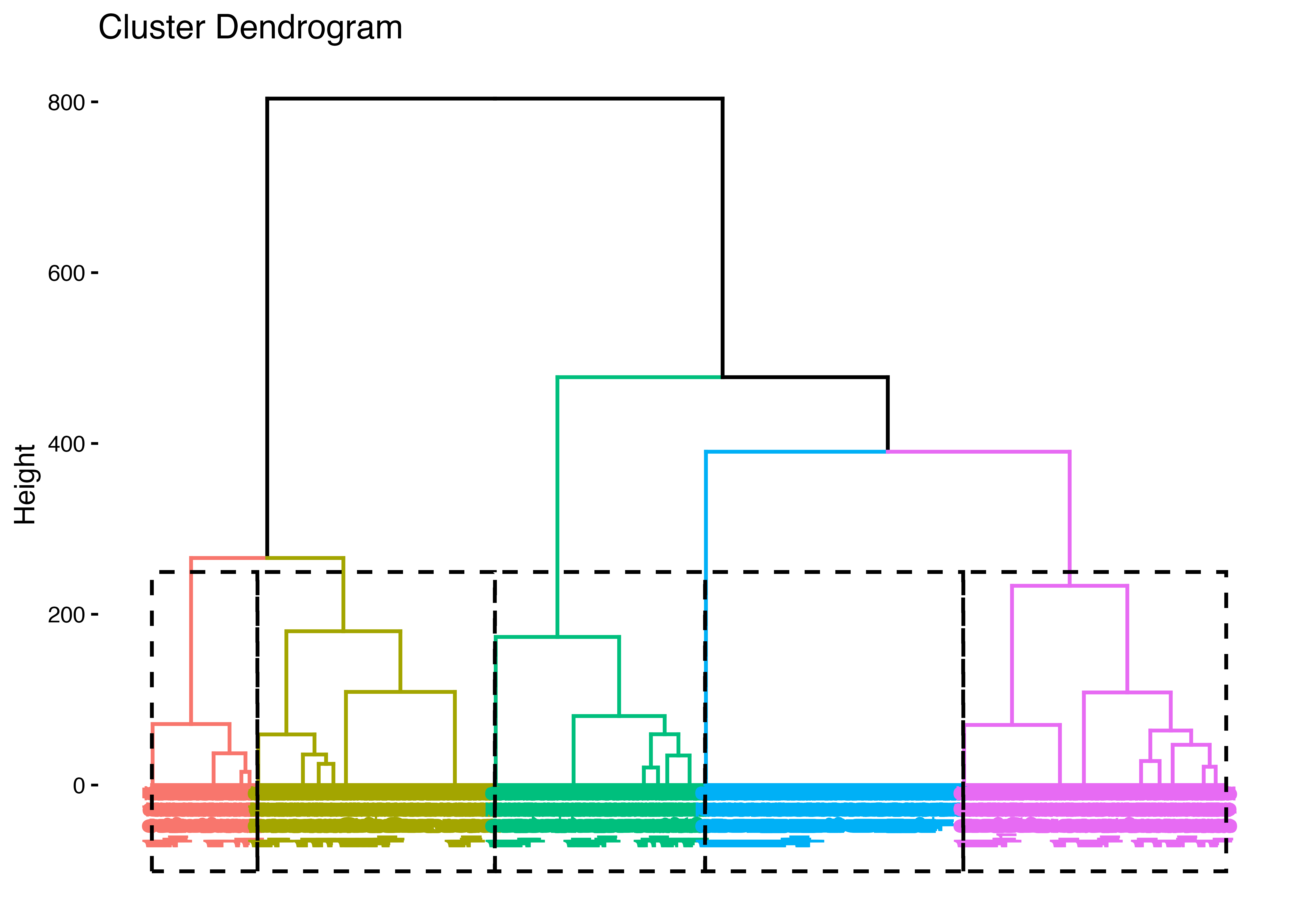
次に，hclust()関数を使って階層的クラスター分析を実行します。 階層別クラスターの分析手順は以下の通りです。

alt_Hier <- clus_cons |>
  dist("euclidian") |> # ユークリッド距離の計算
  hclust("ward.D")  # ウォード法による階層的クラスター分析
alt_Hier |>
  fviz_dend(
    k = 4,  # クラスター数
    rect = TRUE, # クラスター枠の表示
    rect_border = TRUE # クラスター枠の色表示
  )

# コード10-5
fviz_nbclust(
  clus_cons,  # クラスター分析対象データ
  kmeans,  # k-means法
  method = "wss" # クラスター内変動の総和
  )

alt_Hier |>
  fviz_dend(
    k = 5, # クラスター数
    rect = TRUE, # クラスター枠の表示
    rect_border = TRUE # クラスター枠の色表示
  )

# 乱数の種を設定
set.seed(343)

# k-means法による非階層的クラスター分析
K_shopping <- kmeans(clus_cons, 5)
K_shopping
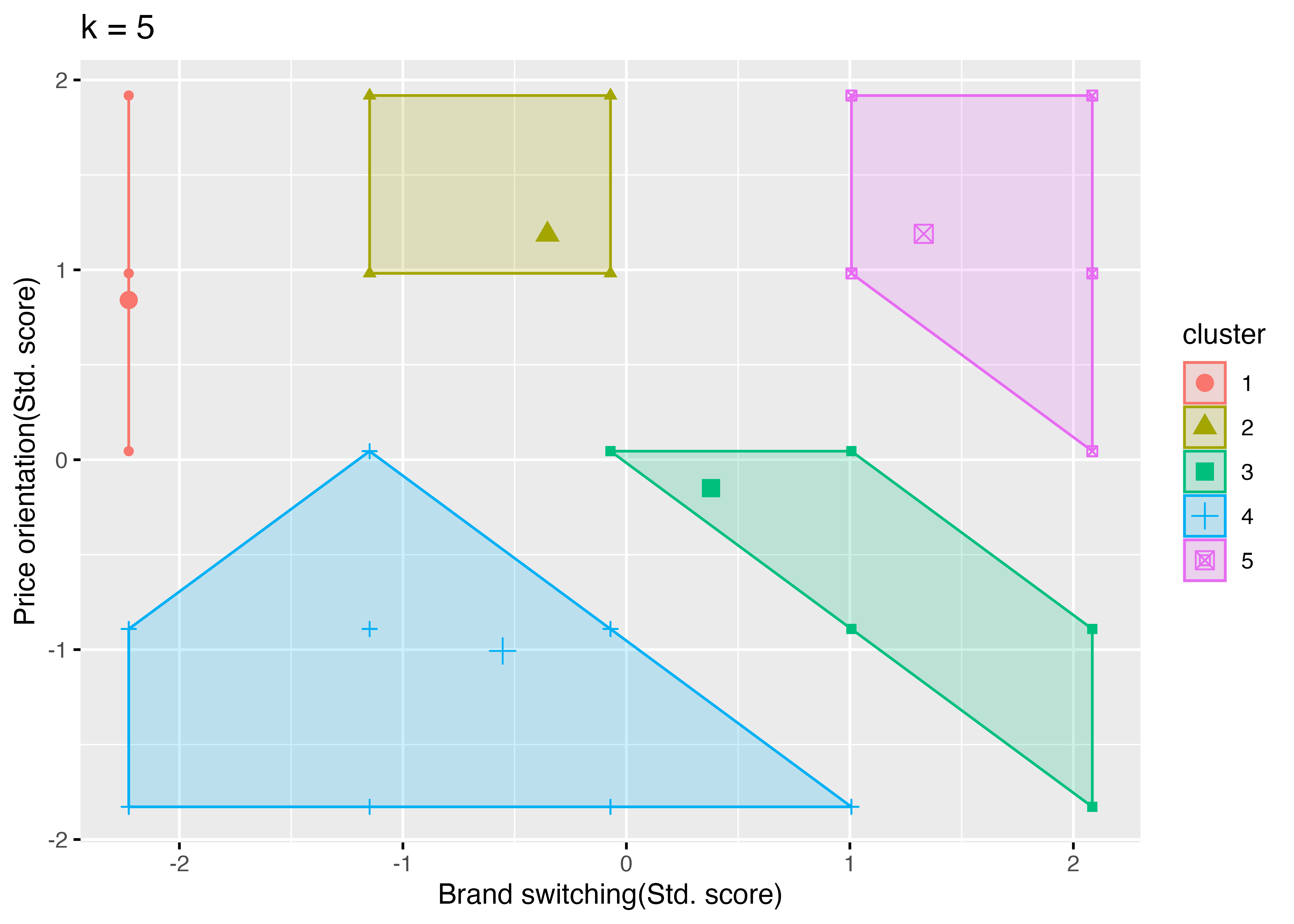
K-means clustering with 5 clusters of sizes 80, 298, 760, 592, 243

Cluster means:
     q12_4    q13_3
1 1.000000 3.850000
2 2.738255 4.218121
3 3.417105 2.792105
4 2.552365 1.876689
5 4.300412 4.222222

Clustering vector:
   [1] 5 5 5 4 3 3 3 4 2 3 3 1 3 3 3 3 4 3 3 4 2 4 5 3 2 4 3 4 5 4 3 3 3 4 3 4 3
  [38] 4 3 3 4 5 4 3 3 4 3 3 4 2 4 2 2 4 4 2 3 3 3 3 4 3 4 3 2 1 2 1 3 4 3 4 2 4
  [75] 2 3 5 3 4 4 4 3 4 3 2 4 3 2 3 3 3 3 4 2 3 3 3 4 4 3 3 3 4 3 3 3 4 4 3 1 3
 [112] 3 3 3 4 4 3 4 5 4 4 5 3 3 4 3 4 4 4 3 3 3 4 1 2 4 3 2 3 1 4 3 2 4 3 3 4 4
 [149] 3 2 5 2 4 2 3 3 3 4 3 3 4 3 4 4 3 4 4 3 3 4 4 3 2 4 5 3 2 4 3 4 3 3 3 3 3
 [186] 4 3 3 3 3 3 2 4 3 3 2 4 4 4 3 2 3 3 4 4 1 3 3 2 4 3 5 3 3 3 4 4 5 3 2 1 4
 [223] 5 3 5 3 4 4 5 3 4 5 3 4 3 3 4 4 5 3 3 3 5 4 3 4 2 3 2 4 3 4 3 3 4 5 4 2 3
 [260] 3 3 3 5 2 5 4 3 2 3 5 1 4 2 3 4 3 4 3 4 3 2 1 3 3 3 2 3 4 4 2 3 4 3 4 4 3
 [297] 3 3 2 4 3 5 4 2 2 4 4 4 4 5 3 1 3 4 4 4 3 3 5 4 5 4 4 3 2 2 4 4 5 4 3 4 5
 [334] 3 3 4 4 3 3 3 2 1 4 3 4 3 4 3 5 5 2 3 1 2 1 3 3 3 4 2 3 4 4 2 3 3 2 2 3 3
 [371] 4 3 3 3 3 3 3 5 3 3 4 4 3 4 3 2 4 3 4 5 3 2 4 2 3 3 4 3 3 3 3 4 4 4 1 4 3
 [408] 4 3 2 3 3 3 3 3 4 3 1 2 4 2 5 2 3 2 3 2 4 2 3 2 3 4 3 3 3 3 3 2 3 4 3 3 3
 [445] 3 3 3 5 3 3 3 1 3 3 4 4 3 2 3 5 3 4 1 5 4 4 3 2 3 3 4 3 5 4 3 4 4 3 3 4 5
 [482] 4 3 4 2 3 5 4 4 4 3 4 3 4 3 3 4 5 5 3 3 3 5 3 3 1 5 3 4 3 4 5 3 2 2 5 5 3
 [519] 2 3 3 4 2 4 3 3 3 2 5 2 4 5 5 3 3 5 3 4 2 3 3 3 3 3 3 4 4 1 4 3 3 4 2 5 4
 [556] 3 4 3 3 2 5 4 5 3 3 4 5 4 3 2 2 4 4 3 2 4 2 3 2 3 3 2 3 3 3 4 5 3 4 3 3 4
 [593] 2 4 3 3 4 3 4 3 4 3 3 4 3 2 2 3 3 3 2 4 3 4 2 5 5 3 5 3 3 5 3 4 3 1 3 2 3
 [630] 3 5 1 4 3 5 3 2 3 2 4 5 2 3 1 4 4 3 2 4 3 4 3 4 3 2 4 3 4 4 3 4 3 5 4 3 3
 [667] 3 3 3 5 2 3 2 3 4 4 3 5 3 3 4 1 3 4 1 3 5 3 5 4 5 3 3 4 2 3 3 5 2 3 3 3 4
 [704] 3 3 4 3 3 3 3 3 5 4 1 2 3 2 4 2 2 3 5 3 3 3 5 3 4 3 5 3 2 3 4 4 5 4 3 1 3
 [741] 4 3 5 4 3 1 3 3 4 4 3 5 4 3 4 4 4 2 3 4 3 5 3 3 3 4 4 3 1 3 5 2 4 1 2 3 2
 [778] 3 2 3 4 3 5 5 4 3 4 4 3 2 3 3 3 1 3 3 3 3 2 4 4 3 3 2 3 4 4 3 3 4 3 5 4 3
 [815] 4 3 4 1 4 1 4 3 4 5 2 4 2 3 4 3 2 5 4 3 4 4 3 4 2 5 3 2 2 4 3 4 4 4 4 3 5
 [852] 3 2 4 5 4 4 5 2 2 3 1 3 4 5 5 3 2 3 3 5 2 4 3 3 2 4 2 3 1 3 2 2 2 3 2 5 1
 [889] 4 4 5 5 5 4 2 5 2 3 4 1 4 3 5 5 3 2 4 4 4 3 2 2 4 3 3 4 3 3 3 3 3 2 3 2 3
 [926] 5 5 4 3 4 3 4 4 3 1 2 4 5 4 3 5 1 2 4 5 4 4 5 3 3 4 3 4 4 3 4 2 4 2 4 5 4
 [963] 3 2 4 5 4 2 4 2 3 4 3 4 3 2 4 2 3 2 3 4 2 4 2 3 3 3 2 2 4 1 3 4 1 4 3 4 4
[1000] 3 5 4 2 5 4 5 2 3 3 3 4 3 4 3 3 4 3 3 4 4 2 3 3 5 3 2 5 3 3 3 3 4 3 4 4 5
[1037] 2 4 3 4 2 3 2 2 4 3 3 3 4 4 2 5 3 3 3 4 3 3 5 4 4 4 2 3 4 5 1 4 3 1 2 5 4
[1074] 4 3 4 5 4 4 3 4 3 3 4 4 4 3 3 3 4 2 4 2 4 3 2 4 4 3 3 2 3 5 5 4 3 3 5 3 4
[1111] 2 2 3 4 5 3 4 5 4 4 3 3 3 3 3 3 4 4 3 3 4 4 3 3 4 3 2 4 5 5 5 5 2 4 3 4 3
[1148] 4 4 2 5 4 3 2 2 3 2 4 3 3 4 4 5 3 2 2 3 4 4 2 4 5 3 5 1 4 3 2 5 3 4 4 3 3
[1185] 4 1 5 2 4 5 3 3 4 4 3 4 3 5 5 2 3 2 3 4 4 3 2 4 4 3 2 4 3 3 3 2 5 4 1 3 5
[1222] 4 4 3 3 3 3 4 4 2 3 4 2 5 5 4 5 4 5 2 5 2 5 4 3 3 4 3 5 3 4 4 3 4 4 4 3 3
[1259] 2 4 2 3 4 4 4 3 4 2 4 2 4 3 4 3 2 2 4 5 5 4 3 3 3 4 4 2 3 3 4 4 3 3 5 1 4
[1296] 3 4 3 2 3 4 3 3 4 5 3 3 4 3 4 3 2 4 4 3 3 3 5 3 4 3 5 4 4 3 4 3 5 1 4 3 1
[1333] 2 4 4 5 3 4 4 3 3 3 4 3 3 5 4 3 1 3 3 5 3 3 3 4 2 3 5 3 2 4 3 4 1 3 4 1 5
[1370] 3 4 3 3 3 4 3 3 5 4 5 4 3 4 2 4 5 2 4 3 3 5 5 3 2 4 5 4 4 3 3 2 3 2 2 3 3
[1407] 4 4 5 3 4 2 3 2 3 1 2 1 2 3 2 3 3 3 4 4 1 4 2 5 3 5 2 4 4 3 4 4 4 5 3 2 3
[1444] 1 5 3 4 3 3 3 2 4 3 4 4 3 4 3 2 4 3 4 2 4 3 3 5 4 3 5 4 2 5 4 4 2 3 2 3 3
[1481] 3 2 5 5 5 4 4 1 3 4 3 4 3 2 5 3 4 3 3 5 1 4 4 4 3 3 3 3 4 3 4 3 4 2 3 3 3
[1518] 3 5 4 5 5 3 2 4 3 4 4 3 3 4 3 4 3 3 2 4 4 4 5 2 4 4 1 3 3 3 5 3 3 5 3 3 3
[1555] 3 5 4 3 2 2 4 3 3 2 3 3 3 3 3 4 4 5 5 4 2 4 3 2 3 4 4 3 1 4 2 1 5 4 2 4 3
[1592] 3 2 3 3 4 5 3 2 2 4 1 3 2 5 3 3 3 2 4 5 5 5 4 3 5 5 4 2 4 3 5 3 1 4 5 3 2
[1629] 4 5 5 3 2 3 3 4 1 3 5 2 3 3 2 4 3 2 3 2 3 5 3 2 2 5 3 2 4 4 4 3 4 2 4 2 3
[1666] 2 4 2 5 5 1 3 4 2 3 5 3 3 5 5 3 4 4 2 2 4 2 4 3 4 4 4 3 3 2 2 2 4 5 2 3 3
[1703] 5 1 3 4 5 2 3 5 5 3 2 2 4 3 3 5 3 4 4 3 3 5 3 4 4 4 3 3 4 4 5 4 4 3 3 3 3
[1740] 4 3 3 4 2 2 5 3 4 4 2 3 4 4 2 4 3 3 2 3 2 4 2 4 4 4 4 5 2 2 3 4 3 2 4 2 4
[1777] 4 4 4 4 3 2 4 4 3 4 4 5 4 5 2 2 2 2 3 5 4 5 2 2 1 4 4 2 4 1 3 5 2 4 5 3 1
[1814] 3 5 4 2 3 3 3 3 2 4 3 5 3 5 3 4 1 5 5 2 3 4 2 5 4 3 5 4 5 3 4 3 4 5 3 4 4
[1851] 4 3 3 5 1 2 5 3 3 1 2 4 3 4 3 3 4 4 1 5 3 3 3 4 1 2 3 5 5 2 4 3 2 4 4 2 3
[1888] 2 4 5 4 3 2 3 5 3 1 3 2 3 1 2 3 2 4 3 3 3 3 4 4 3 4 4 3 4 2 4 2 3 3 5 3 4
[1925] 5 3 4 3 4 4 5 4 1 4 3 3 3 2 2 5 1 4 4 3 3 3 4 4 4 4 2 4 3 4 1 4 5 2 4 3 5
[1962] 1 3 3 3 4 5 2 3 3 4 3 3

Within cluster sum of squares by cluster:
[1]  54.2000 108.4060 401.9303 622.3750 127.0700
 (between_SS / total_SS =  66.7 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"      
# コード10-8

fviz_cluster(
  K_shopping,  # k-means法の結果
  data = clus_cons, # クラスター分析対象データ
  geom = "point" # プロットの形状
  ) +
  labs( # タイトルと軸ラベル
    title = "k = 5",
    x = "Brand switching(Std. score)",
    y = "Price orientation(Std. score)"
  )

# コード10-9
df_cons$cluster_id <- factor(K_shopping$cluster)

knitr::kable(head(df_cons), caption = "結合データ")
結合データ
県番号 性別 年齢 結婚有無 q12_4 q13_3 Pref Gender MaritalSt. cluster_id
13 2 38 2 4 4 Tokyo Female Not Married 5
13 1 42 2 4 5 Tokyo Male Not Married 5
13 1 30 1 5 4 Tokyo Male Married 5
13 1 33 1 2 1 Tokyo Male Married 4
28 1 25 1 3 3 Hyogo Male Married 3
28 1 32 1 3 3 Hyogo Male Married 3 
# コード10-10

clus_summary <- df_cons |>
  group_by(cluster_id) |>
  summarize(
    N = n(),
    Loyalty_m = mean(q12_4),
    Price_m   = mean(q13_3),
    Age_m     = mean(年齢),
    Male_r    = sum(Gender == "Male") / n(),
    Tokyo_r   = (sum(Pref == "Tokyo") / n()) / (1465 / 1973),
    Married_r = sum(MaritalSt. == "Married") / n()
  )
# 表示
knitr::kable(clus_summary, caption = "クラスターサマリー")
クラスターサマリー
cluster_id N Loyalty_m Price_m Age_m Male_r Tokyo_r Married_r
1 80 1.000000 3.850000 42.61250 0.5125000 0.8753925 0.5250000
2 298 2.738255 4.218121 38.56040 0.5134228 0.9400188 0.6107383
3 760 3.417105 2.792105 41.88816 0.5065789 1.0100683 0.5618421
4 592 2.552365 1.876689 43.79730 0.4645270 1.0191680 0.4712838
5 243 4.300412 4.222222 34.91770 0.5102881 1.0363938 0.6213992
Back to top