5 第7章 回帰分析上の工夫
ここでは、次のような回帰分析を行う上で役立ついくつかの工夫について説明しています。
- ダミー変数
- 交差項
- 係数比較
- 対数変換
準備として、必要なパッケージとデータを読み込みます。 データはMktRes_firmdata.xlsxを使用し、2019年のデータに絞り込みます。
-
pacman::p_load()で各種パッケージを読み込みます。インストールされていない場合は自動的にインストールされます。 -
readxl::read_xlsx()関数でExcelファイルを読み込みんで、firmdataデータフレームに格納します。 -
dplyr::filter()関数で2019年のデータに絞り込んで、firmdata19データフレームに格納します。
次に小売業を表すための変数を作成します。 産業名を表す変数ind_enの値を見てみましょう。
Code
firmdata19$ind_en |>
table() |> # 表形式にして
as.data.frame() |> # データフレームに変換
arrange(desc(Freq)) |> # 頻度順に並び替え
knitr::kable() |> # 表として表示
# 1行目と4行目と5行目を太字にして、背景を薄い青にする。
kableExtra::row_spec(1, bold = TRUE, background = "#D6EAF8") |>
kableExtra::row_spec(4, bold = TRUE, background = "#D6EAF8") |>
kableExtra::row_spec(5, bold = TRUE, background = "#D6EAF8")| Var1 | Freq |
|---|---|
| Retail Stores, NEC | 36 |
| Miscellaneous Services | 30 |
| Railroad (Major) | 27 |
| Supermarket Chains | 13 |
| Department Stores | 7 |
| Hotels | 5 |
| Air Transportation | 4 |
| Amusement Services | 4 |
| Motor Vehicles | 4 |
| Communication Services | 2 |
| Cosmetics & Toilet Goods | 2 |
| Home & Pre-Fabs | 2 |
| Miscellaneous Wholesales | 2 |
| Railroad (Minor) | 2 |
| Bakery Products | 1 |
| Foods, NEC | 1 |
| Musical Instrument | 1 |
| Real Estate - Sales | 1 |
| Trucking | 1 |
| Wholesale - Foods | 1 |
ind_enには20種類の産業があることが分かります。 このうち、本書ではRetial Stores, NEC、Supermarket Chains、Department Storesの3つを小売業と定義しています。 これらの産業をretailというベクトルにまとめます。
変数ind_enの値がretailに含まれる業種ならRetail、そうでなければOtherとなる変数formatを作成します。 ここでは、dplyrパッケージのmutate()関数とif_else()関数を使って新しい変数formatを作成します。
%in%演算子は、左側の値が右側のベクトルに含まれているかどうかを論理値(TRUEまたはFALSE)で返します。 これを使って、ind_enの各値がretailベクトルに含まれているかどうかをチェックしています。
作成されたformat変数の型を確認します。
formatは文字列(character)であることが確認できました。 次に、変数formatのカテゴリーごとの企業数を確認します。 with()関数とtable()関数を使って、カテゴリーごとの企業数を確認します。
with()関数は、データフレーム内の変数を直接参照できるようにするための関数です。 つまりwith(データフレーム, 式)の形式で使用すると、式内でデータフレームの変数名を直接使うことができ、いちいちデータフレーム$変数名と書かなくても済みます。 ここでは、firmdata19データフレーム内のformat変数を参照しています。
次に、format変数を使って、営業利益率opを従属変数、マーケティング費用mkexpとformatを独立変数とした回帰モデルを推定します。
ここで、「format」変数は「Retail」か「Other」という2種類の文字が入ってる文字列やん!ダミー変数ちゃうやん!と思った人は素晴らしい。その通りです。 しかし、Rのlm()関数は、自動的に文字列やカテゴリ変数をダミー変数に変換して回帰分析を行ってくれます。したがって、ここでは特にダミー変数に変換せず、そのままformat変数を使って回帰分析を行っています。教科書p.200で解説しています。
summary()関数を使ってfirmdata19の記述統計量を見てみると、やはりformat変数が文字列であるため、何も計算されていません。 カテゴリー変数であることをRに認識させるために、format変数を因子型(factor)に変換してもよいですし、そもそもformat変数を作成する際に、0と1のダミー変数として作成してもよいです。
fyear legalname ind_en parent
Min. :2019 Length:146 Length:146 Length:146
1st Qu.:2019 Class :character Class :character Class :character
Median :2019 Mode :character Mode :character Mode :character
Mean :2019
3rd Qu.:2019
Max. :2019
fiscal_month current_liability ltloans total_liability
Length:146 Min. : 2692 Min. : 0 Min. : 5599
Class :character 1st Qu.: 37359 1st Qu.: 2753 1st Qu.: 66080
Mode :character Median : 117196 Median : 41204 Median : 239226
Mean : 495040 Mean : 220643 Mean : 1061859
3rd Qu.: 476658 3rd Qu.: 300356 3rd Qu.: 1132916
Max. :8065246 Max. :3408119 Max. :12551936
current_assets ppent total_assets net_assets_per_capital
Min. : 2810 Min. : 323 Min. : 15356 Min. : 596
1st Qu.: 51266 1st Qu.: 43240 1st Qu.: 134457 1st Qu.: 76602
Median : 140754 Median : 173550 Median : 444356 Median : 191336
Mean : 569153 Mean : 886708 Mean : 1706754 Mean : 644895
3rd Qu.: 406981 3rd Qu.: 895231 3rd Qu.: 1983718 3rd Qu.: 809614
Max. :10675939 Max. :6962034 Max. :16976709 Max. :4424773
sales sga operating_profit net_profit
Min. : 11333 Min. : 1064 Min. :-40469 Min. :-666178
1st Qu.: 183525 1st Qu.: 47240 1st Qu.: 7743 1st Qu.: 3716
Median : 464450 Median : 123030 Median : 23904 Median : 13875
Mean :1199403 Mean : 302043 Mean : 81088 Mean : 41716
3rd Qu.:1164243 3rd Qu.: 256828 3rd Qu.: 63068 3rd Qu.: 43376
Max. :9878866 Max. :2919902 Max. :656163 Max. : 404319
pnet_profit re adv labor_cost
Min. :-671216 Min. : -2125 Min. : 0 Min. : 261
1st Qu.: 3713 1st Qu.: 56655 1st Qu.: 0 1st Qu.: 15454
Median : 12979 Median : 134356 Median : 0 Median : 43877
Mean : 39353 Mean : 485602 Mean : 19100 Mean : 101114
3rd Qu.: 35303 3rd Qu.: 539003 3rd Qu.: 12904 3rd Qu.: 91691
Max. : 397881 Max. :4125043 Max. :280801 Max. :1221504
rd other_sg emp temp
Min. : 0 Min. : 424 Min. : 163 Min. : 70
1st Qu.: 0 1st Qu.: 15425 1st Qu.: 3454 1st Qu.: 3490
Median : 0 Median : 38320 Median : 7826 Median : 8450
Mean : 1554 Mean : 95539 Mean : 20249 Mean : 18274
3rd Qu.: 0 3rd Qu.:103514 3rd Qu.: 24464 3rd Qu.: 17510
Max. :148080 Max. :744106 Max. :160227 Max. :259938
tempratio indgrowth adint rdint
Min. :0.04768 Min. :-0.05099 Min. :0.00000 Min. :0.00000
1st Qu.:0.29308 1st Qu.:-0.01298 1st Qu.:0.00000 1st Qu.:0.00000
Median :0.51187 Median : 0.01703 Median :0.00000 Median :0.00000
Mean :0.49349 Mean : 0.02609 Mean :0.01372 Mean :0.00065
3rd Qu.:0.65912 3rd Qu.: 0.05098 3rd Qu.:0.02120 3rd Qu.:0.00000
Max. :0.90313 Max. : 0.08349 Max. :0.12879 Max. :0.04245
mkexp op roa format
Min. :0.01137 Min. :-0.01567 Min. :-0.11539 Length:146
1st Qu.:0.16714 1st Qu.: 0.03080 1st Qu.: 0.01671 Class :character
Median :0.25448 Median : 0.05916 Median : 0.02729 Mode :character
Mean :0.29868 Mean : 0.06979 Mean : 0.03083
3rd Qu.:0.37506 3rd Qu.: 0.09967 3rd Qu.: 0.04630
Max. :0.75650 Max. : 0.35571 Max. : 0.19965 このカテゴリー変数formatを使って回帰分析を行います。
op_i = \beta_0 + \beta_1 mkexp_i + \beta_2 format_i + \varepsilon_i
formatをRtailのとき1、Otherのとき0となるダミー変数として捉えると、上の式は次のように表現できます。
\begin{aligned} \mathrm{E}[op_i \mid Retail = 1] &= \beta_0 + \beta_1 kexp_i + \beta _2\\ &= (\beta_0 + \beta_2) + \beta_1 mkexp_i \\ \mathrm{E}[op_i \mid Retail = 0] &= \beta_0 + \beta_1 mkexp_i \end{aligned}\\
formatの回帰係数\beta_2は、切片の差を表しています。 回帰分析の結果を見ながら、切片の差を確認しましょう。
code 7-2 ダミー変数を使った回帰分析
| (1) | |
|---|---|
| * p | |
| (Intercept) | 0.102*** |
| (0.009) | |
| mkexp | -0.066*** |
| (0.025) | |
| formatRetail | -0.032*** |
| (0.009) | |
| Num.Obs. | 146 |
| R2 | 0.138 |
| R2 Adj. | 0.126 |
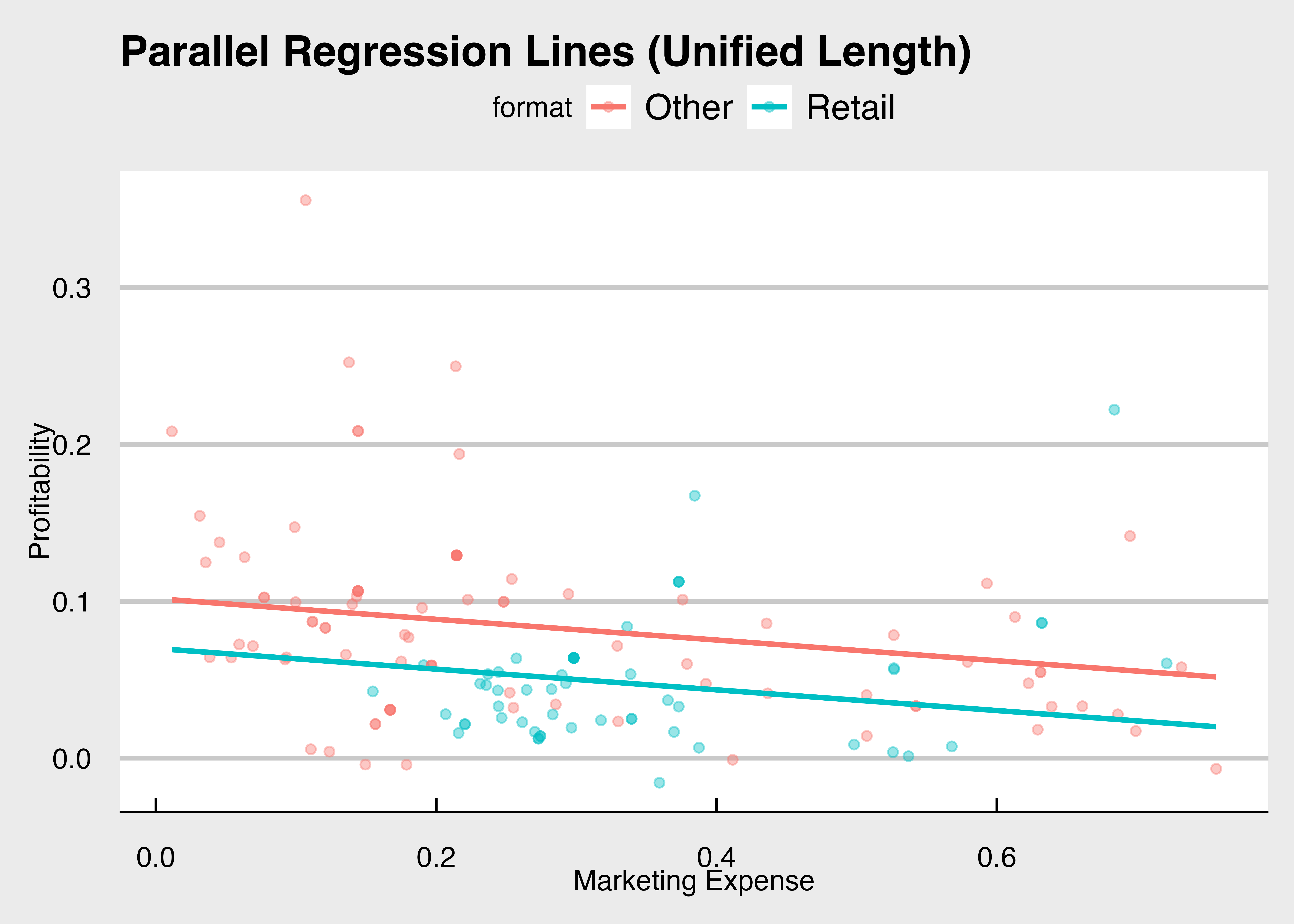
これを図にすると、次のようになります。
Code
切片だけが異なる回帰直線のプロット
# mkexpの全範囲をカバーするグリッドを、全format分作成します
grid_data <- expand_grid(
mkexp = seq(min(firmdata19$mkexp, na.rm = TRUE),
max(firmdata19$mkexp, na.rm = TRUE),
length.out = 100),
format = unique(firmdata19$format)
)
# 3. このグリッドに対して予測値を計算
grid_data$pred <- predict(fit.d1, newdata = grid_data)
# 4. プロット
ggplot(firmdata19, aes(x = mkexp, y = op, color = format)) +
geom_point(alpha = 0.4) +
# データの範囲に関わらず、grid_dataに基づいて線を引く
geom_line(data = grid_data, aes(y = pred), size = 1) +
labs(
title = "Parallel Regression Lines (Unified Length)",
x = "Marketing Expense",
y = "Profitability"
) +
theme_economist_white()5.1 交差項
説明変数Xが大きくなると、従属変数Yも大きくなる、という関係があり、その関係は変数Zの値によって変わる、という場合があります。 このような変数間の関係に影響を与える効果を相互作用効果(interaction effect)といいます。 経営学の研究では非常によく使われるモデルの仕様です。
5.1.1 傾きダミー
変数Zの値によって、回帰直線の切片や傾きが変わる場合を考えます。 次のような回帰モデルを考えます。
op_i = \beta_0 + \beta_1 mkexp_i + \beta_2 retail_i + \beta_3 mkexp_i \times retail_i +\varepsilon_i
先ほどと同様に、retailを小売業を表すダミー変数です。 したがって、上の式は次のように表現できます。
\begin{aligned} \mathrm{E}[op_i \mid retail = 1] &= \beta_0 + \beta_1 mkexp_i + \beta_2 + \beta_3 mkexp_i \\ &= (\beta_0 + \beta_2) + (\beta_1 + \beta_3) mkexp_i \\ \mathrm{E}[op_i \mid retail = 0] &= \beta_0 + \beta_1 mkexp_i \end{aligned}
小売業か否かで差があるのなら、切片だと\beta_2、傾きだと\beta_3が有意になるはず、と考えられます。 では、実際に回帰分析を行ってみましょう。 交差項を回帰モデルに組み込むには、:演算子または*演算子を使います。
-
:演算子は、指定した2つの変数の交差項のみをモデルに含めます。 -
*演算子は、指定した2つの変数の主効果と交差項の両方をモデルに含めます。
交差項のみを入れる場合というのはあまりないので、通常は*演算子を使って主効果と交差項の両方をモデルに含めます。
回帰分析の結果を見てみましょう。
| (1) | (2) | (3) | |
|---|---|---|---|
| * p | |||
| (Intercept) | 0.102*** | 0.095*** | 0.113*** |
| (0.009) | (0.009) | (0.009) | |
| mkexp | -0.066*** | -0.066** | -0.107*** |
| (0.025) | (0.027) | (0.027) | |
| formatRetail | -0.032*** | -0.099*** | |
| (0.009) | (0.022) | ||
| mkexp × formatRetail | -0.045* | 0.206*** | |
| (0.027) | (0.060) | ||
| Num.Obs. | 146 | 146 | 146 |
| R2 | 0.138 | 0.086 | 0.203 |
| R2 Adj. | 0.126 | 0.073 | 0.186 |
一番左のモデル1は切片ダミーのみ、中央のモデル2は傾きダミーのみ、右のモデル3は切片ダミーと傾きダミーの両方を含んでいます。 回帰係数も決定係数R^2も大きく異なっていることが分かります。適切なモデルを使っているかどうかで、分析結果が大きく変わることが分かります。
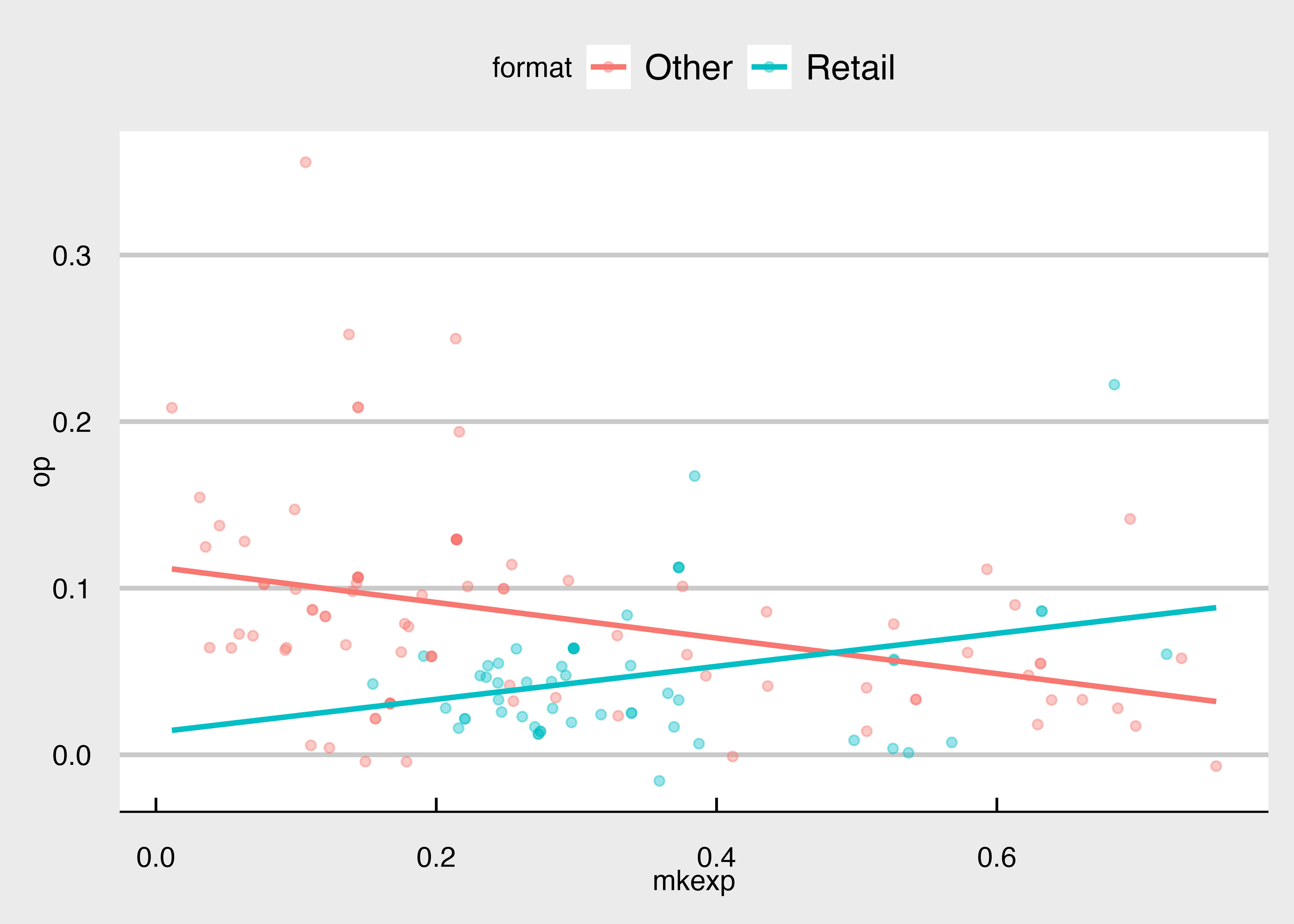
モデル3の結果を図にしてみましょう。
Code
交差項を含む回帰直線のプロット
# mkexpの全範囲をカバーするグリッドを、全format分作成します
grid_data <- expand_grid(
mkexp = seq(min(firmdata19$mkexp, na.rm = TRUE),
max(firmdata19$mkexp, na.rm = TRUE),
length.out = 100),
format = unique(firmdata19$format)
)
# 予測値を計算
grid_data$pred <- predict(fit.d3, newdata = grid_data)
# プロット
ggplot(firmdata19, aes(x = mkexp, y = op, color = format)) +
geom_point(alpha = 0.4) +
geom_line(data = grid_data, aes(y = pred), size = 1)+
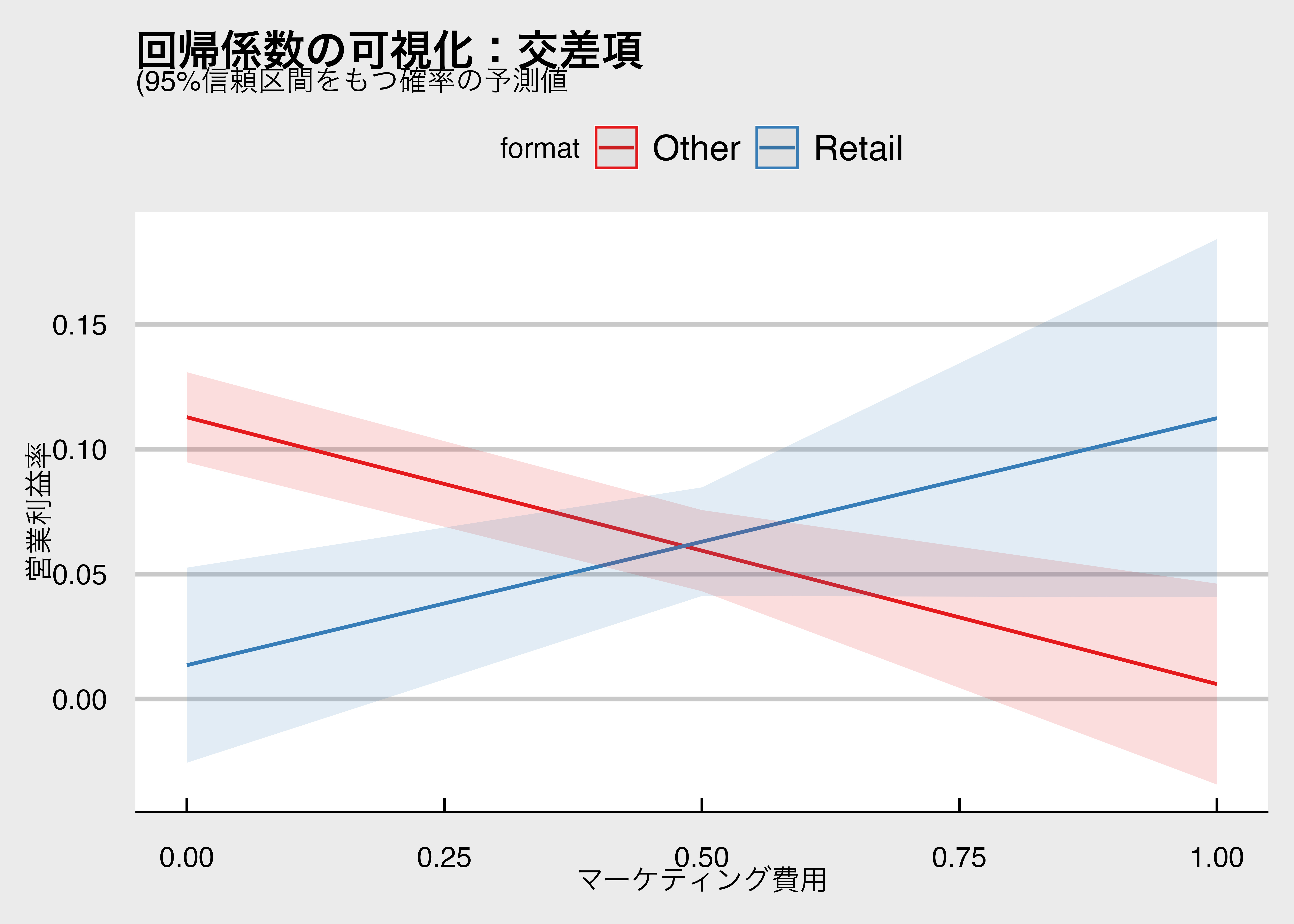
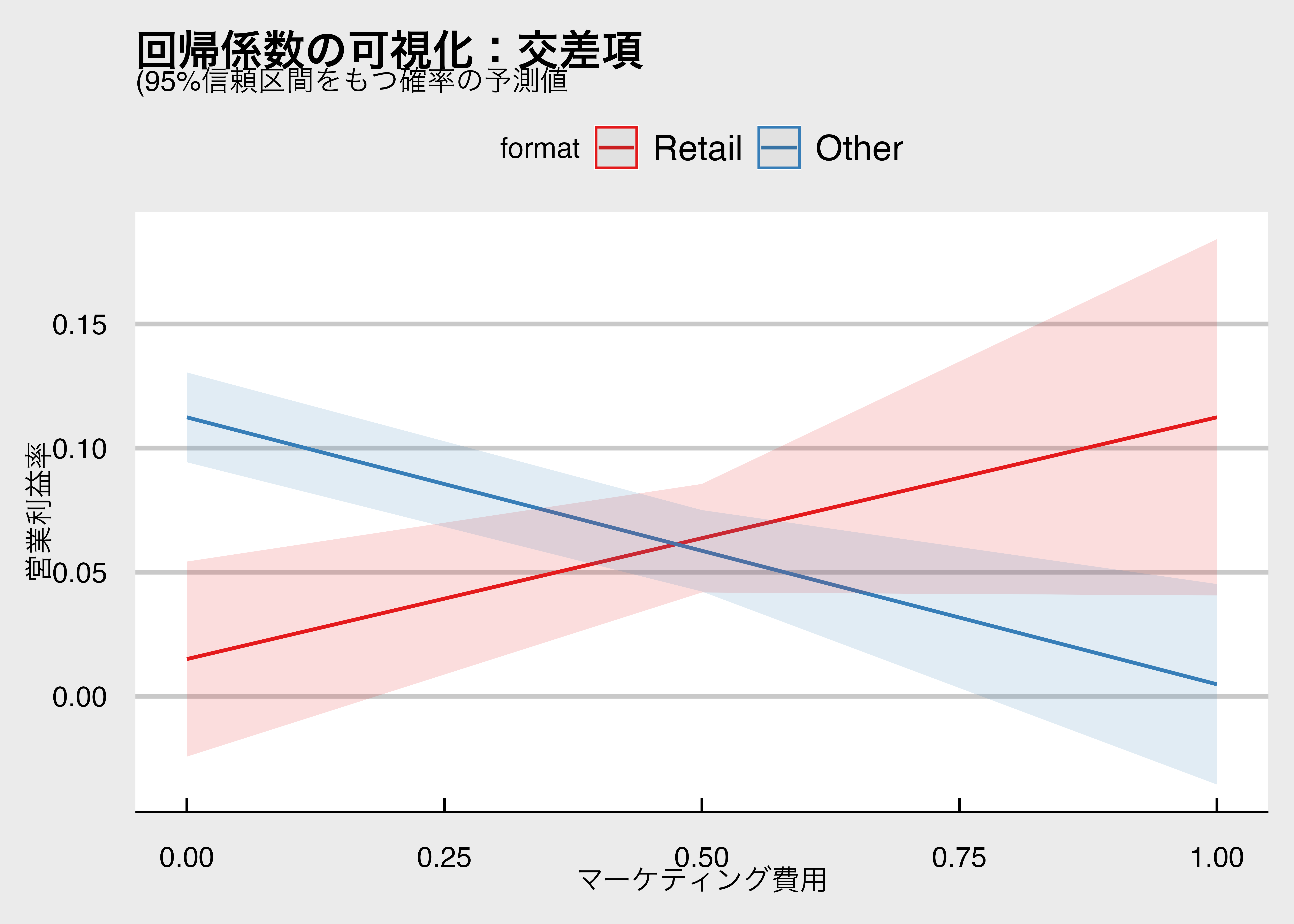
theme_economist_white()交差項の分析結果を可視化するために、sjPlotパッケージのplot_model()関数を使います。 引数type = "pred"を指定すると、予測値の周辺平均(marginal mean)をプロットできます。つまり全ての観測値が小売業とみなしたときに得られる予測値の平均値です。ようするに条件付期待値なので、上の図と同じです。
code 7-6 交差項の可視化
回帰分析の結果から、小売業ダミーとマーケティング支出の交差項が統計的に有意に正であることから、小売業はその他業種とは異なり、マーケティング支出の増加が営業利益率にプラスの与える、ということが言えます。
しかし、交差項の信頼区間を見てみると、マーケティング費用が低いときは、業種間んで差がありそうだけれど、マーケティング費用が高いときは、業種間で差が出たのはたまたまかもしれない、ということも分かります。
これだけだと,上の図と違いが分かりませんが,重回帰分析の結果でも同様の図を書けます。 独立変数が2つになると,散布図が次のような三次元の図になります。 plotlyパッケージを使うと,インタラクティブな三次元散布図が描けます。 マーケティング費用mkexpと広告宣伝費advを独立変数,営業利益率opを従属変数とした三次元散布図を描いてみましょう。 三次元散布図に回帰平面を追加しています。
Code
三次元散布図の例
library(plotly)
# 1. データの準備
# format を因子(カテゴリ)として明示的に変換します
# ※ データの中に "Retail", "Other" という文字列が入っていると仮定します
firmdata19$format <- factor(firmdata19$format, levels = c("Retail", "Other"))
# 2. 交互作用モデルの構築
# op = mkexp + adv + mkexp * format (傾きが format によって変わるモデル)
multi_dummy <- lm(op ~ mkexp + adv + mkexp * format, data = firmdata19)
# 3. 予測用グリッド(軸)の作成
mk_seq <- seq(min(firmdata19$mkexp, na.rm=T), max(firmdata19$mkexp, na.rm=T), length.out = 30)
ad_seq <- seq(min(firmdata19$adv, na.rm=T), max(firmdata19$adv, na.rm=T), length.out = 30)
# ---------------------------------------------------------
# 4. 「Retail」用の予測平面データの作成
# ---------------------------------------------------------
grid_retail <- expand.grid(mkexp = mk_seq, adv = ad_seq)
grid_retail$format <- factor("Retail", levels = levels(firmdata19$format)) # Retailに固定
# 予測して行列化
z_retail_vec <- predict(multi_dummy, newdata = grid_retail)
z_retail <- matrix(z_retail_vec, nrow = 30, ncol = 30)
# ---------------------------------------------------------
# 5. 「Other」用の予測平面データの作成
# ---------------------------------------------------------
grid_other <- expand.grid(mkexp = mk_seq, adv = ad_seq)
grid_other$format <- factor("Other", levels = levels(firmdata19$format)) # Otherに固定
# 予測して行列化
z_other_vec <- predict(multi_dummy, newdata = grid_other)
z_other <- matrix(z_other_vec, nrow = 30, ncol = 30)
# ---------------------------------------------------------
# 6. プロット(2枚の平面を重ねる)
# ---------------------------------------------------------
fig <- plot_ly(firmdata19, x = ~mkexp, y = ~adv, z = ~op) %>%
# 実測値のプロット(formatごとに色分けすると見やすいです)
add_markers(color = ~format, colors = c('blue', 'red'),
marker = list(size = 3, opacity = 0.5), name = ~format) %>%
# 1枚目:Retailの回帰平面(青系)
add_surface(x = ~mk_seq, y = ~ad_seq, z = ~t(z_retail),
opacity = 0.5,
colorscale = list(c(0, 1), c("lightblue", "blue")),
showscale = FALSE, # カラーバーを消す
name = "Regression (Retail)") %>%
# 2枚目:Otherの回帰平面(赤系)
add_surface(x = ~mk_seq, y = ~ad_seq, z = ~t(z_other),
opacity = 0.5,
colorscale = list(c(0, 1), c("pink", "red")),
showscale = FALSE,
name = "Regression (Other)") %>%
layout(scene = list(xaxis = list(title = 'マーケ費用'),
yaxis = list(title = '広告宣伝費'),
zaxis = list(title = '営業利益率')),
title = "店舗形態別(Retail/Other)の回帰平面")
figこのような多次元空間の回帰式における交差項の効果を取り出して可視化も可能です。
5.1.2 連続変数の交差項
連続変数同士の交差項もよく使われますが,ダミー変数同士の交差項やダミー変数と連続変数の交差項にはない注意点があります。
y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 z_{i} + \beta_3 x_{i} \times z_{i} + \varepsilon_i
という回帰式を考え,xやzが微少に変化したときのyの変化量を考えるため,上の関数をxやzで偏微分すると,
\begin{aligned} \frac{\partial y_i}{\partial x_i} = \beta_1 + \beta_3 z_i \\ \frac{\partial y_i}{\partial z_i} = \beta_2 + \beta_3 x_i \end{aligned}
となり,xやzがyに与える影響は,それぞれzやxの値によって変わることが分かります。
5.1.3 注意点1
\beta_1はz_i = 0のときのxがyに与える影響を表しますが,z_i=0という値が適切でない場合もあります。 そこで,変数を平均値で中心化(centering)してから交差項を作成することがよく行われます。
この論文では中心化の効果を数学的証明と実証データの両面からみている。
5.1.4 数学的・理論的根拠
- 行列の行列式の不変性: 非中心化データの積行列 X'X の行列式と、平均中心化データの積行列の行列式は同一で,多重共線性による計算上の問題は行列式の値がゼロに近づくことで発生するため、平均中心化をしてもこの状況は変わらない。
- 統計的同等性: 平均中心化は単に座標軸の起点を移動させるだけであり、データ点同士の相対的な位置関係は変わらない。
- 推計値の同一性: 以下の要素は、平均中心化の有無に関わらず、計算精度、点推定値、標準誤差ともに全く同じ(あるいは数学的に変換可能で同等)であることが証明されている。
- 交互作用項の係数とその標準誤差
- モデル全体の決定係数(R^2)
- 主効果および単純効果(一方が分かればもう一方を正確に算出可能) ### 実証的根拠
例としてあげられているブランド拡張の評価に関する実データを用いた分析では、以下のことが示されている。
- 見かけ上の変化: 未中心化データでは不自然な負の係数が出た変数が、平均中心化によって正の係数に変わった
- 解釈の相違: これは共線性が解決したからではなく「係数の意味」が変わったため
- 未中心化の係数は「他方が0の時の単純効果」を、中心化後の係数は「平均的なレベルにおける主効果」を表しているに過ぎない
この論文を参照 https://pubsonline.informs.org/doi/epdf/10.1287/mksc.1060.0263
\begin{aligned} \frac{\partial y_i}{\partial x_i} = \beta_1 + \beta_3 z_i \end{aligned}
Rows: 221
Columns: 4
$ ID <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1…
$ sales <dbl> 118.8377, 548.6312, 197.3075, 104.2657, 748.8251, 947.8850, …
$ rd <dbl> 404.0893, 252.1270, 444.3374, 407.5876, 841.7605, 336.8744, …
$ promotion <dbl> 75.63163, 102.74572, 97.98040, 83.46613, 105.69250, 80.17476…
Call:
lm(formula = sales ~ rd * promotion, data = Headphone07)
Residuals:
Min 1Q Median 3Q Max
-46.522 -12.861 -0.638 13.578 70.667
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.033e+04 1.090e+02 186.5 <2e-16 ***
rd -5.187e+01 2.844e-01 -182.4 <2e-16 ***
promotion -1.914e+02 1.052e+00 -181.9 <2e-16 ***
rd:promotion 4.979e-01 2.730e-03 182.4 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 20.55 on 217 degrees of freedom
Multiple R-squared: 0.9935, Adjusted R-squared: 0.9934
F-statistic: 1.111e+04 on 3 and 217 DF, p-value: < 2.2e-16
Call:
lm(formula = sales ~ rd_c * promotion_c, data = Headphone07)
Residuals:
Min 1Q Median 3Q Max
-46.522 -12.861 -0.638 13.578 70.667
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 382.27812 1.51459 252.40 <2e-16 ***
rd_c -0.91767 0.01196 -76.75 <2e-16 ***
promotion_c 0.69039 0.03972 17.38 <2e-16 ***
rd_c:promotion_c 0.49792 0.00273 182.37 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 20.55 on 217 degrees of freedom
Multiple R-squared: 0.9935, Adjusted R-squared: 0.9934
F-statistic: 1.111e+04 on 3 and 217 DF, p-value: < 2.2e-16# コード7-11
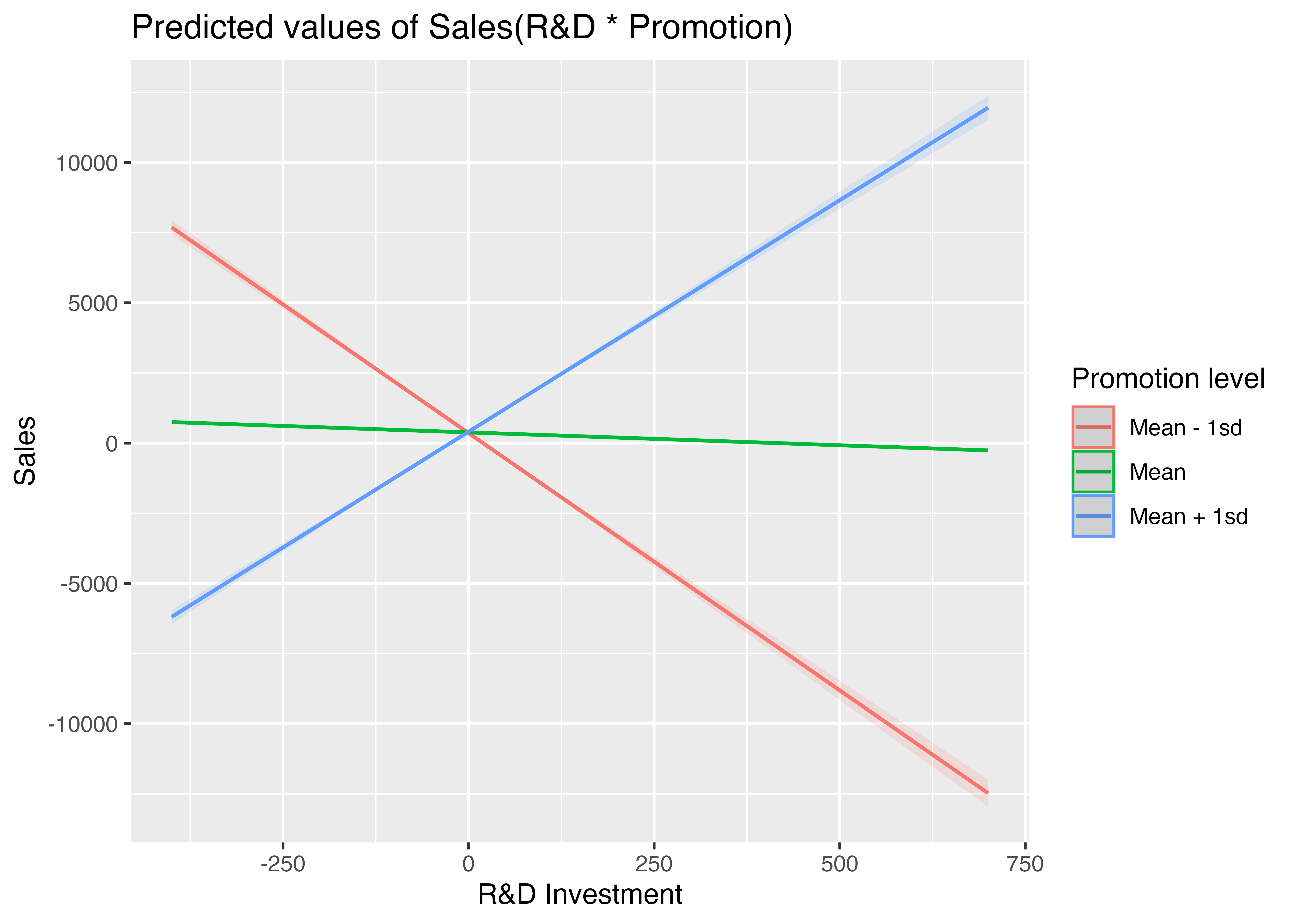
leg = c("Mean - 1sd", "Mean", "Mean + 1sd")
int_fig1 <- plot_model(fit_int_c,
type = "int",
mdrt.values = "meansd",
ci.lvl = .9999999999) +
labs(
title = "Predicted values of Sales(R&D * Promotion)",
x = "R&D Investment",
y = "Sales") +
scale_color_discrete(
name = "Promotion level",
labels = leg)
int_fig1# コード7-12
# install.packages("marginaleffects")
# コード7-13
# library(marginaleffects)
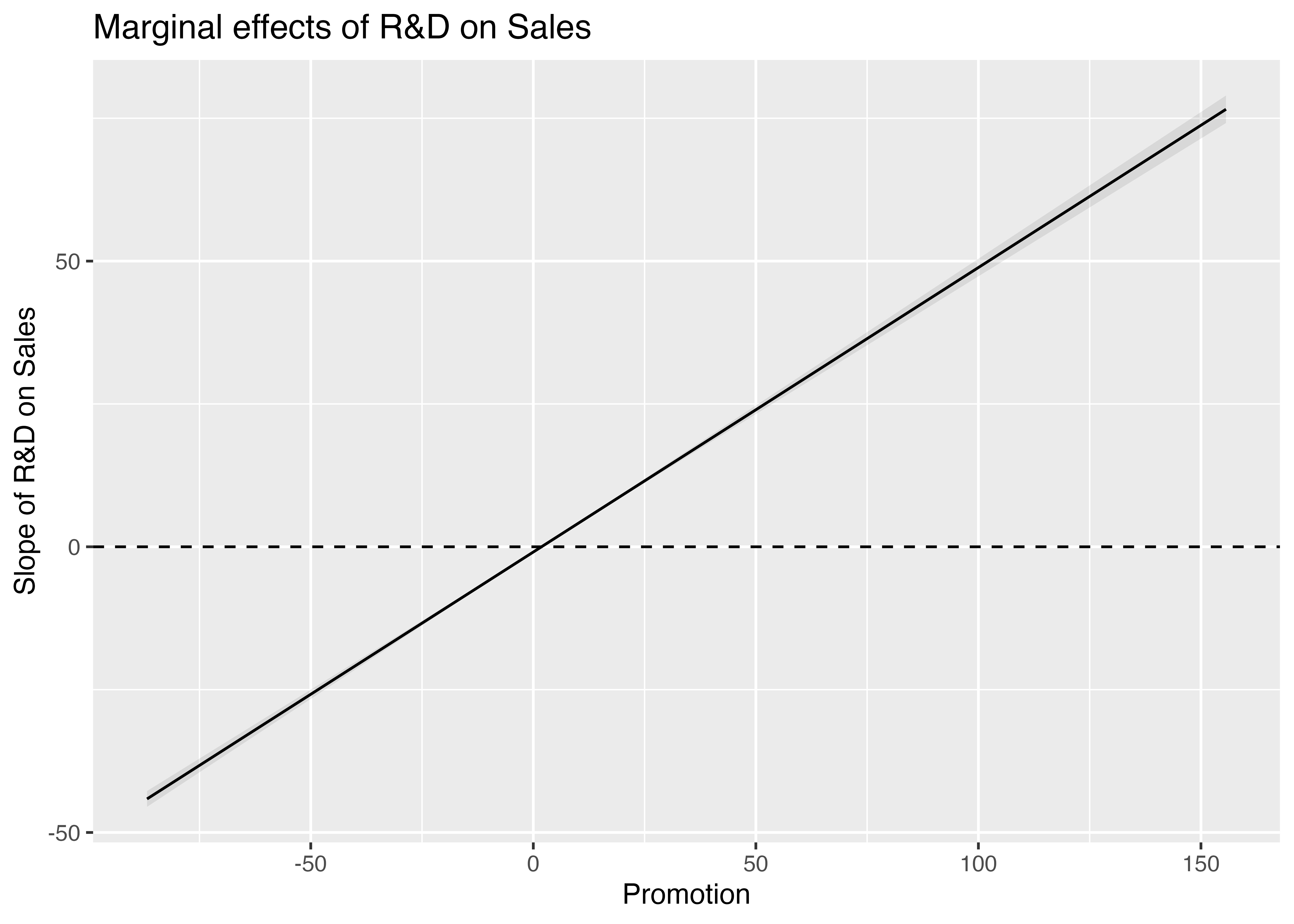
int_fig2 <- plot_slopes(fit_int_c, variables = "rd_c",
condition = "promotion_c", conf_level = .99999999) +
labs(title = "Marginal effects of R&D on Sales",
x = "Promotion", y = "Slope of R&D on Sales") +
geom_hline(aes(yintercept = 0), linetype = "dashed")
int_fig2# コード7-14
firmdata19 <- firmdata19 %>%
mutate(mkexp_c = mkexp - mean(mkexp),
asset_c = total_assets - mean(total_assets))
fit_int2 <- lm(op ~ mkexp_c * asset_c, data = firmdata19)
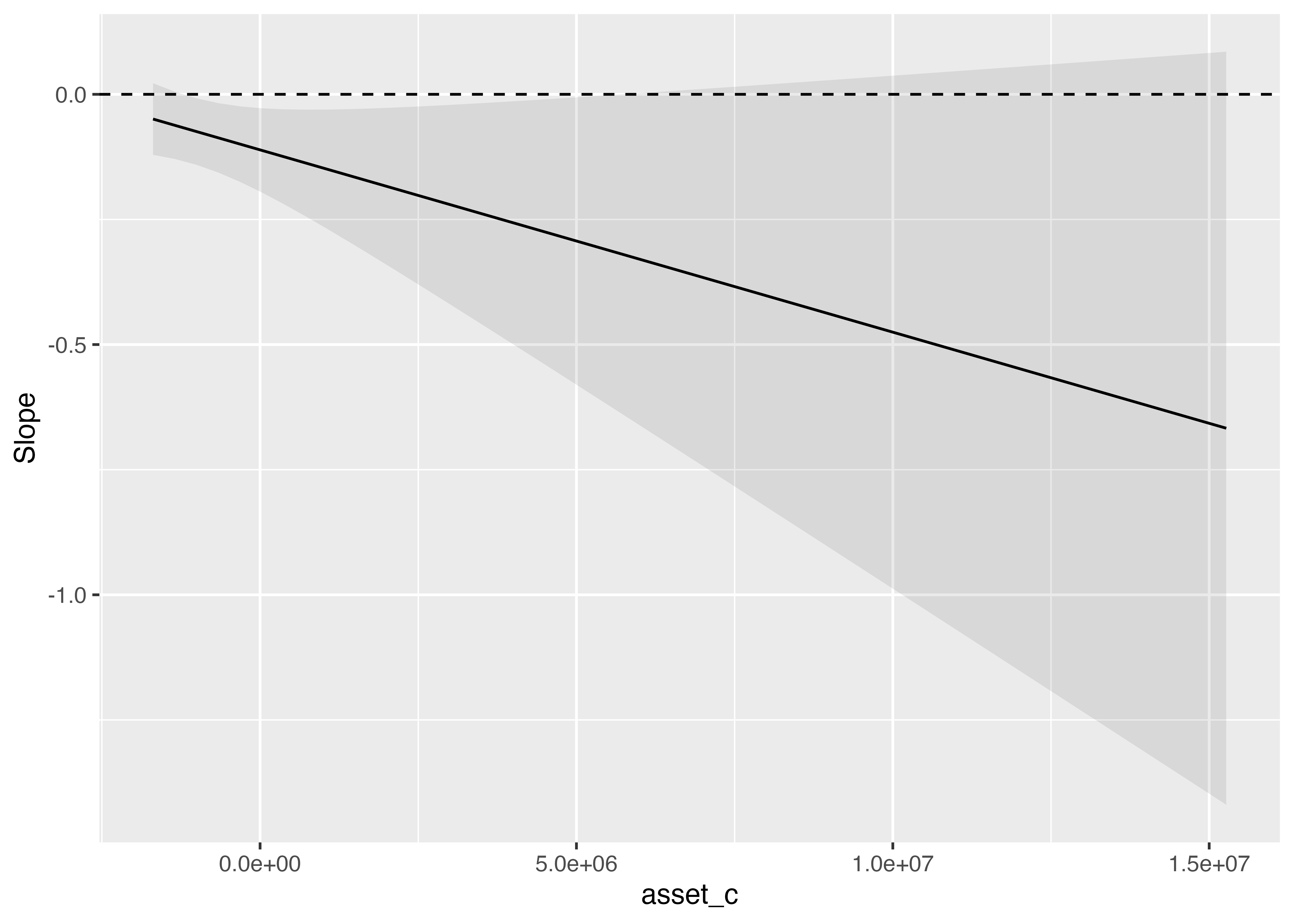
int_fig3 <- plot_slopes(fit_int2, variables = "mkexp_c",
condition = "asset_c", conf_level = 0.99) +
geom_hline(aes(yintercept = 0), linetype = "dashed")
int_fig3
Call:
lm(formula = sales ~ adv + rd, data = firmdata19)
Residuals:
Min 1Q Median 3Q Max
-4357995 -463348 -236824 123663 2692251
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1199403 74285 16.146 <2e-16 ***
adv 1632326 74996 21.766 <2e-16 ***
rd 29915 74996 0.399 0.691
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 897600 on 143 degrees of freedom
Multiple R-squared: 0.7711, Adjusted R-squared: 0.7679
F-statistic: 240.8 on 2 and 143 DF, p-value: < 2.2e-16
Call:
lm(formula = sales ~ adv + ad_rd, data = firmdata19)
Residuals:
Min 1Q Median 3Q Max
-4357995 -463348 -236824 123663 2692251
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1199403 74285 16.146 <2e-16 ***
adv 1602411 111739 14.341 <2e-16 ***
ad_rd 29915 74996 0.399 0.691
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 897600 on 143 degrees of freedom
Multiple R-squared: 0.7711, Adjusted R-squared: 0.7679
F-statistic: 240.8 on 2 and 143 DF, p-value: < 2.2e-16
Call:
lm(formula = log(sales) ~ log(labor_cost) + log(ppent), data = firmdata19)
Residuals:
Min 1Q Median 3Q Max
-1.40821 -0.36129 -0.00933 0.38591 1.66673
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.17129 0.31733 9.994 <2e-16 ***
log(labor_cost) 0.53739 0.03679 14.605 <2e-16 ***
log(ppent) 0.34588 0.02797 12.366 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5169 on 143 degrees of freedom
Multiple R-squared: 0.8747, Adjusted R-squared: 0.8729
F-statistic: 499.1 on 2 and 143 DF, p-value: < 2.2e-16
Call:
lm(formula = log(q) ~ log(p), data = price)
Residuals:
Min 1Q Median 3Q Max
-1.11220 -0.13668 0.02804 0.16166 0.51039
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.47781 0.08135 116.5 <2e-16 ***
log(p) -0.18008 0.01354 -13.3 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2309 on 998 degrees of freedom
Multiple R-squared: 0.1506, Adjusted R-squared: 0.1497
F-statistic: 176.9 on 1 and 998 DF, p-value: < 2.2e-16
Linear hypothesis test:
log(p) = - 1
Model 1: restricted model
Model 2: log(q) ~ log(p)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 999 248.811
2 998 53.225 1 195.59 3667.3 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1| (1) | |
|---|---|
| (Intercept) | 20326.588 |
| [20111.797, 20541.378] | |
| rd | -51.872 |
| [-52.433, -51.312] | |
| promotion | -191.431 |
| [-193.505, -189.358] | |
| rd × promotion | 0.498 |
| [0.493, 0.503] | |
| Num.Obs. | 221 |
| R2 | 0.994 |
| R2 Adj. | 0.993 |
| AIC | 1969.2 |
| BIC | 1986.2 |
| Log.Lik. | -979.617 |
| F | 11110.648 |
| RMSE | 20.36 |
| (1) | |
|---|---|
| (Intercept) | 20326.588 |
| (108.978) | |
| rd | -51.872 |
| (0.284) | |
| promotion | -191.431 |
| (1.052) | |
| rd × promotion | 0.498 |
| (0.003) | |
| Num.Obs. | 221 |
| R2 | 0.994 |
| R2 Adj. | 0.993 |
| F | 11110.648 |
# コード7-24
var_nam <- c("rd" = "R&D", "promotion" = "Promotion",
"rd:promotion" = "R&D * Promotion",
"rd_c" = "R&D_c", "promotion_c" = "Promotion_c",
"rd_c:promotion_c" = "R&D_c * Promotion_c",
"(Intercept)" = "定数項")
Int <- list()
Int[["Without centering"]] <- fit_int
Int[["With centering"]] <- fit_int_c
msummary(Int,
coef_map = var_nam,
title = "Comparing Interaction Models",
notes = "Values in [ ] show 95% confidence intervals",
stars = TRUE,
statistic = 'conf.int', conf_level = .95,
gof_omit = "Log.Lik.|AIC|BIC|RMSE")| Without centering | With centering | |
|---|---|---|
| + p | ||
| Values in [ ] show 95% confidence intervals | ||
| R&D | -51.872*** | |
| [-52.433, -51.312] | ||
| Promotion | -191.431*** | |
| [-193.505, -189.358] | ||
| R&D * Promotion | 0.498*** | |
| [0.493, 0.503] | ||
| R&D_c | -0.918*** | |
| [-0.941, -0.894] | ||
| Promotion_c | 0.690*** | |
| [0.612, 0.769] | ||
| R&D_c * Promotion_c | 0.498*** | |
| [0.493, 0.503] | ||
| 定数項 | 20326.588*** | 382.278*** |
| [20111.797, 20541.378] | [379.293, 385.263] | |
| Num.Obs. | 221 | 221 |
| R2 | 0.994 | 0.994 |
| R2 Adj. | 0.993 | 0.993 |
| F | 11110.648 | 11110.648 |
| Without centering | With centering | |
|---|---|---|
| + p \num{ | ||
| Values in [ ] show 95\% confidence intervals | ||
| (Intercept) | \num{20326.588}*** | \num{382.278}*** |
| [\num{20111.797}, \num{20541.378}] | [\num{379.293}, \num{385.263}] | |
| rd | \num{-51.872}*** | |
| [\num{-52.433}, \num{-51.312}] | ||
| promotion | \num{-191.431}*** | |
| [\num{-193.505}, \num{-189.358}] | ||
| rd × promotion | \num{0.498}*** | |
| [\num{0.493}, \num{0.503}] | ||
| rd\_c | \num{-0.918}*** | |
| [\num{-0.941}, \num{-0.894}] | ||
| promotion\_c | \num{0.690}*** | |
| [\num{0.612}, \num{0.769}] | ||
| rd\_c × promotion\_c | \num{0.498}*** | |
| [\num{0.493}, \num{0.503}] | ||
| Num.Obs. | \num{221} | \num{221} |
| R2 | \num{0.994} | \num{0.994} |
| R2 Adj. | \num{0.993} | \num{0.993} |
| F | \num{11110.648} | \num{11110.648} |