6章は変数間の関係を考察する手法の1つである回帰分析 (Regression Analysis) について説明します。
いま手元に売上高(yとする)と従業員数(xとする)という2つのデータの組 (y_i, x_i) があるとします。 i は企業の番号を表しており,n 社のデータがあるとします。 こんな感じのデータです。
| 1 |
1000 |
5 |
| 2 |
2000 |
10 |
| 3 |
3000 |
15 |
| … |
… |
… |
| n |
4500 |
25 |
n はサンプルサイズといいます。サンプル数という言い方は誤りです。サンプル数は1です。
いま、従業員数xが増えると売上高yは増えるのか否か、という分析をしたいとしましょう。 つまり、従業員数と売上高との間には関係があるのかどうかを調べたい、ということです。 しかし、関係があるといってもいろんな関係がある可能性があります。 そこで、変数間の関係で最も基本的なものとして線形関係 (linear relation) を考えます。
y は x と線形関係であると考え分析のモデルを構築します。 これを「単回帰モデル」と呼び、次のように表します。
y_i = \beta_0 + \beta_1 x_i + u_i
ここで各変数は以下のように定義されます。
-
y_i: 従属変数 (dependent variable)、応答変数、または目的変数。
-
x_i: 独立変数 (independent variable)、または説明変数。
-
\beta_0: 切片 (intercept)。
-
\beta_1: 傾き (slope) または回帰係数。
-
u_i: 誤差項 (error term)。モデルがデータを説明できない確率的な変動部分を表します。
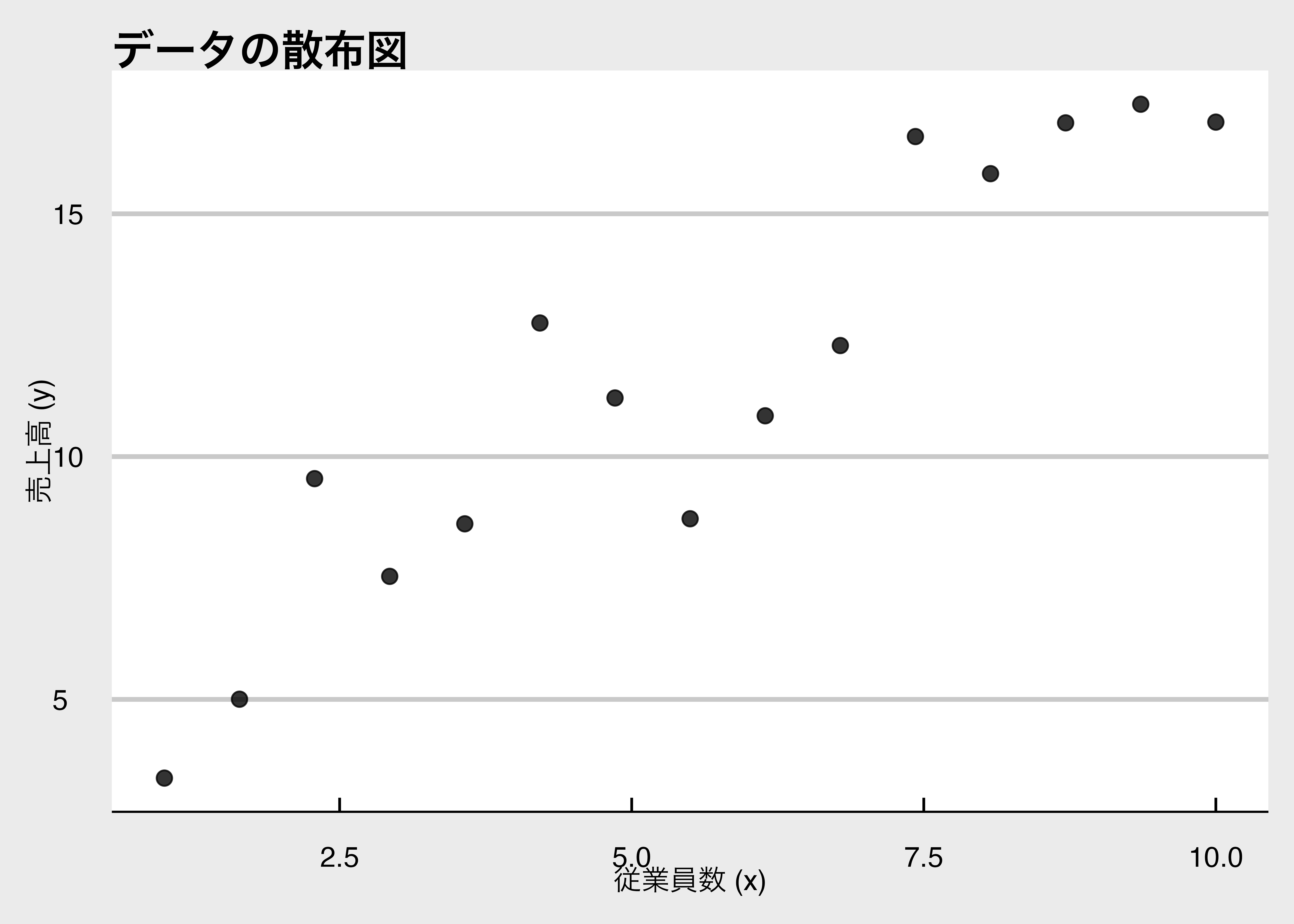
手元にある売上高yと従業員数xのデータを使って、横軸を従業員数、縦軸を売上高とした散布図に描くと次のようになります。
Code
pacman::p_load(tidyverse, ggthemes, GGally, gt, gtExtra, knitr, kableExtra)
set.seed(123) # 乱数のタネ
n <- 15 # サンプルサイズ
x <- seq(1, 10, length.out = n) # 独立変数
y <- 3 + 1.5 * x + rnorm(n, mean = 0, sd = 2) # 従属変数
data <- data.frame(x = x, y = y) # データフレームの作成
my_font <- if (Sys.info()["sysname"] == "Darwin") "HiraKakuProN-W3" else "sans"
# 作図
g <- ggplot(data, aes(x = x, y = y)) +
geom_point(size = 2.5, color = "black", alpha = 0.8) +
theme_economist_white(base_family = my_font) +
labs(
title = "データの散布図",
x = "従業員数 (x)",
y = "売上高 (y)"
)
print(g)
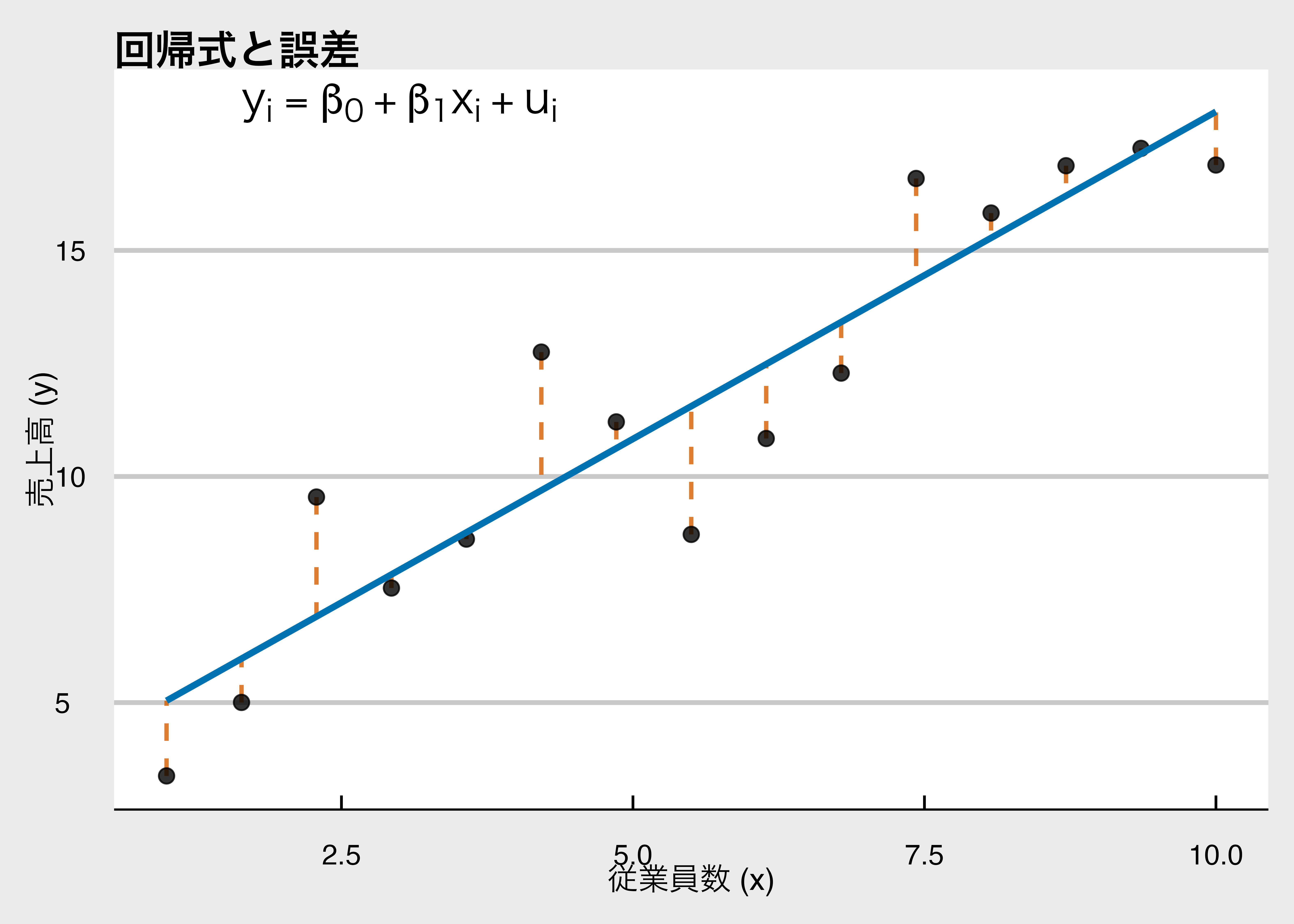
散布図をみると右肩上がりの関係があるように見えますが、もっと明確に変数間の関係を表すために、そのデータを最も良く説明できる直線をひこうと思います。 つまり、切片の\beta_0と傾きの\beta_1を決めるということです。 この直線が「モデル」で、それぞれの黒い点とモデルの直線との縦軸方向への距離を「誤差」または「残差」と呼びます。
Code
model <- lm(y ~ x, data = data)
# 予測値をpredictedに格納
data$predicted <- predict(model)
# OSに合わせてフォントを自動選択(Macならヒラギノ、それ以外ならデフォルト)
g <- ggplot(data, aes(x = x, y = y)) +
geom_segment(
aes(xend = x, yend = predicted),
color = "#D55E00", linetype = "dashed", alpha = 0.8, linewidth = 0.8
) +
geom_point(size = 2.5, color = "black", alpha = 0.8) +
theme_economist_white(base_family = my_font) +
labs(
title = "回帰式と誤差",
x = "従業員数 (x)",
y = "売上高 (y)"
) +
geom_smooth(method = "lm", se = FALSE, color = "#0072B2", linewidth = 1.2) +
theme(
plot.title = element_text(face = "bold", size = 16),
axis.title = element_text(size = 12),
) +
annotate("text",
x = min(data$x) + 2,
y = max(data$y) + 1,
label = "y[i] == beta[0] + beta[1] * x[i] + u[i]",
parse = TRUE,
size = 6, family = my_font
)
print(g)
望ましい性質を備えた直線の引き方の1つとして、ガウス(Gauss)が構築した最小二乗法(Ordinaly Least Square Methods: OLS)について説明します。
分析準備
サンプルデータを読み込みます。 MS Excelのファイル .xlsx なので、readxl::read_xlsx() 関数を使います。 読み込んだデータから、2019年のデータを抽出します。
firmdata <- readxl::read_xlsx("data/MktRes_firmdata.xlsx")
firmdata19 <- firmdata |>
filter(fyear == 2019) # 2019年を抽出
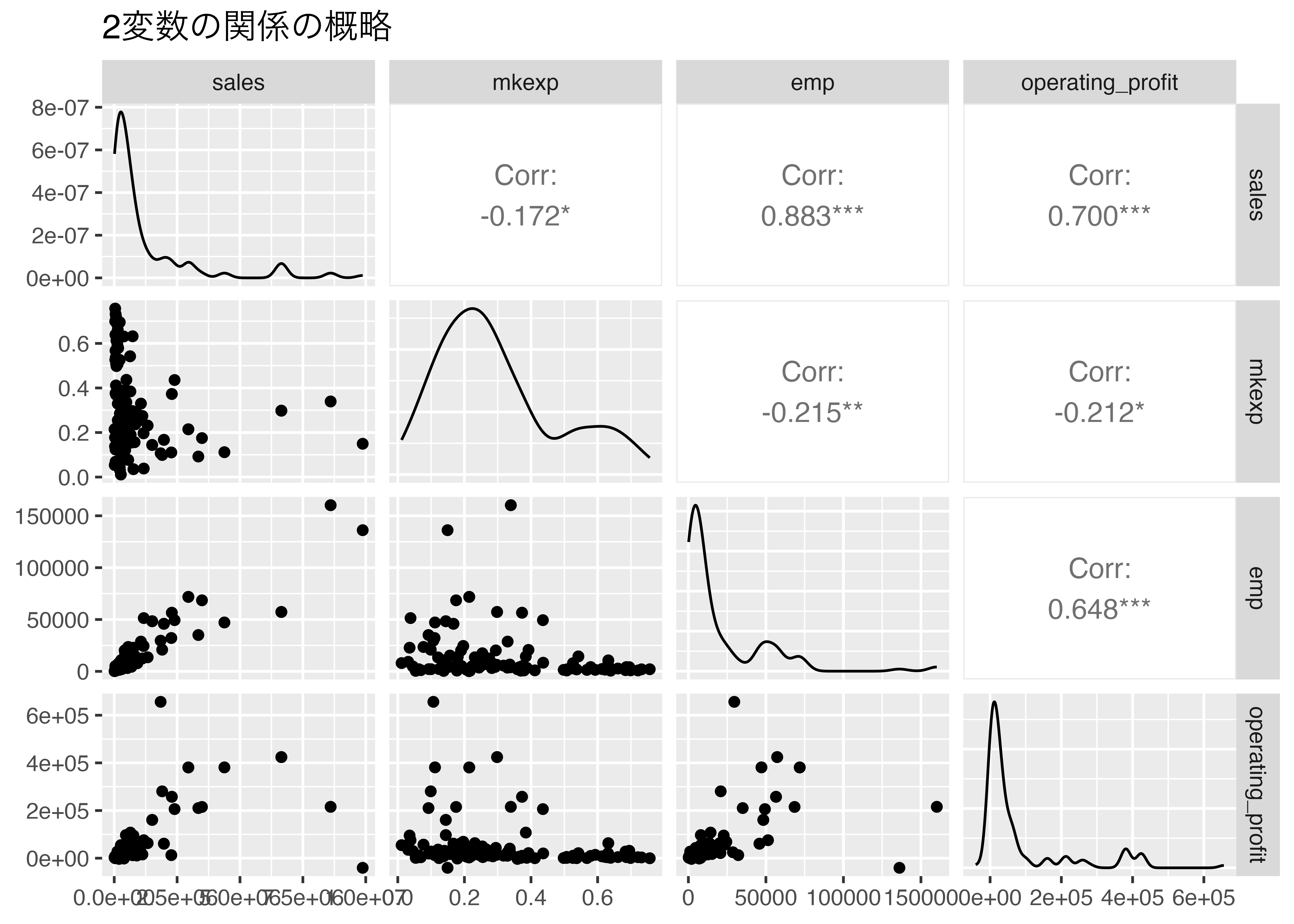
探索的なデータ分析として、変数間の関係を概観するために GGally パッケージの ggpairs() 関数を使います。
firmdata19 |>
select(sales, mkexp, emp, operating_profit) |>
GGally::ggpairs() +
labs(title = "2変数の関係の概略")
出力された図を見てみます。
-
対角線 (分布): 売上高
sales や従業員数 emp、営業利益 operating_profit は値の小さい左側にデータが集まっており、右側に裾を引く歪んだ分布であることがわかります。
-
右上 (相関係数):
Corr: として相関係数が表示されています。売上高 sales と従業員数 emp や営業利益 operating_profit の相関が高く、また営業利益と従業員数にも強い正の相関があります。
-
左下 (散布図): 2変数間の散布図が表示されています。異常値の有無などを確認できます。
こういった図でデータを概観し、線形回帰モデルが適切かどうかを判断したり、異常値の有無を確認して分析結果の解釈に役立てたりします。
次に、図ではなく数値としてデータの特徴をつかむため記述統計量を計算します。 ここでは基本関数 summary() を使って計算します。
ds1 <- firmdata19 |>
select(sales, mkexp, emp, operating_profit) |> # 変数を選択
summary() # 記述統計量
knitr::kable(ds1, align = "cccc") |>
kableExtra::kable_styling(latex_options = "hold_position")
|
Min. : 11333 |
Min. :0.01137 |
Min. : 163 |
Min. :-40469 |
|
1st Qu.: 183525 |
1st Qu.:0.16714 |
1st Qu.: 3454 |
1st Qu.: 7743 |
|
Median : 464450 |
Median :0.25448 |
Median : 7826 |
Median : 23904 |
|
Mean :1199403 |
Mean :0.29868 |
Mean : 20249 |
Mean : 81088 |
|
3rd Qu.:1164243 |
3rd Qu.:0.37506 |
3rd Qu.: 24464 |
3rd Qu.: 63068 |
|
Max. :9878866 |
Max. :0.75650 |
Max. :160227 |
Max. :656163 |
単回帰モデルと予測値
膨大なデータを目の前にした我々は、そのデータを最も良く「説明」できるシンプルなモデルを特定したいと考えます。 最も基本的な関数 f:x \rightarrow y として1次関数を考えます。
y = \beta_0 + \beta_1 x
ここで、\beta_0 は切片、\beta_1 は傾きを表します。 何らかの方法で\beta_0と\beta_1を決めたとしよう。 その切片を \hat{\beta}_0、傾きを \hat{\beta}_1 とします。 x に手元にあるデータ x_i を代入して計算できる値を予測値 (predicted value) といい、\hat{y}_i と表します。
\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_i
このとき、実際の観測値 y_i と予測値 \hat{y}_i の差を残差 (residual) といい、e_i で表します。
e_i = y_i - \hat{y}_i
回帰分析で最も良く用いられており、望ましい性質をもつ推定値を計算できる方法は最小二乗法といい、この残差e_iの二乗和 \sum e_i^2 を最小にするように \hat{\beta}_0 と \hat{\beta}_1 を決定します。
Rでは lm() 関数を使って計算できます。 ここでは、売上高が従業員数で説明できるかを調べる単回帰モデルを構築します。
sales_i = \beta_0 + \beta_1 emp_i + u_i
Rだと従属変数 ~ 独立変数という形で回帰式を指定します。
# 回帰モデルを構築
ols_model <- "sales ~ emp" # 回帰式の定義
モデルを最小自乗法で推定するには、lm()関数を使います。 lm()関数の第1引数に回帰式を、第2引数にデータフレームを指定します。 推定結果をreg1というオブジェクトに格納し、回帰係数を表示するにはcoef()関数を使います。
reg1 <- lm(formula = ols_model, data = firmdata19)
coef(reg1) # 回帰係数
(Intercept) emp
22113.98050 58.14081
最小二乗法で推定された係数は以下のようになります。
\hat{sales}_i = 22113.98050 + 58.14081 \times emp_i
従業員が10名のときの売上高の予測値は22695.3886となり、従業員が1名増えるごとに売上高が約58.14増加すると予測されます。
回帰分析における推定と検定
回帰分析と統計的推測
この節は回帰分析の理屈を学習する上で重要な章なので、時間を掛けて学習することをオススメします。
企業データを用いた回帰分析の実行
上で推定した回帰分析の結果をみていきます。 lm()関数で推定した結果をreg1というオブジェクトに格納しているので、その中身をみてみましょう。 詳細を表示するにはsummary()関数を使います。
summary()関数は引数に指定するオブジェクトの型により異なる結果を返します。 ここでは、lmオブジェクトを引数に指定しているので、回帰分析の結果が表示されます。
Call:
lm(formula = ols_model, data = firmdata19)
Residuals:
Min 1Q Median 3Q Max
-1834902 -280228 -34549 136598 3292521
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 22113.980 89224.761 0.248 0.805
emp 58.141 2.569 22.628 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 875800 on 144 degrees of freedom
Multiple R-squared: 0.7805, Adjusted R-squared: 0.779
F-statistic: 512 on 1 and 144 DF, p-value: < 2.2e-16
confint(reg1, level = 0.99)
0.5 % 99.5 %
(Intercept) -210798.52845 255026.48944
emp 51.43362 64.84799
回帰係数の解釈
この節は難しいので、教科書の解説に補足を加えながら説明します。 例として次のような重回帰モデルを考えます。
y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + u_i
ここでx_{1i}の微少な変化がy_iに与える影響を知りたいとします。 この回帰モデルをx_{1i}で偏微分すると、次のようになります。
\frac{\partial y_i}{\partial x_{1i}} = \beta_1
つまりx_{2i}を一定としてx_{1i}が1単位変化した場合のy_iの変化量は\beta_1である、ということです。このことを他の変数を一定とした場合の効果 (ceteris paribus effect) といい、様々な要因で決定されているであろう従属変数に対して、特定の独立変数が与える影響を測定する際に重要な考え方となります。
単回帰モデルと重回帰モデルの比較
営業利益operating_profitを従属変数、広告宣伝費advを独立変数とした単回帰モデルを推定します。
reg2 <- lm(operating_profit ~ adv, data = firmdata19)
summary(reg2)
Call:
lm(formula = operating_profit ~ adv, data = firmdata19)
Residuals:
Min 1Q Median 3Q Max
-450526 -55552 -40672 -791 599084
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.708e+04 1.057e+04 5.401 2.68e-07 ***
adv 1.257e+00 2.159e-01 5.823 3.61e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 117600 on 144 degrees of freedom
Multiple R-squared: 0.1906, Adjusted R-squared: 0.185
F-statistic: 33.91 on 1 and 144 DF, p-value: 3.613e-08
confint()関数を使って信頼区間を計算します。
2.5 % 97.5 %
(Intercept) 36189.311039 77968.894422
adv 0.830362 1.683719
次に、営業利益operating_profitを従属変数、広告宣伝費adv、温度temp、従業員数emp、労働費用labor_cost、総資産total_assets、研究開発費rdを独立変数とした重回帰モデルを推定します。 教科書とは異なりますが、先にモデルを定義してからlm()関数に渡す方法で推定します。
multi_model <- "operating_profit ~ adv + temp + emp + labor_cost + total_assets + rd"
この回帰モデルをlm()関数で推定し、結果をsummary()関数で表示します。
reg3 <- lm(formula = multi_model, data = firmdata19)
summary(reg3)
Call:
lm(formula = multi_model, data = firmdata19)
Residuals:
Min 1Q Median 3Q Max
-360544 -27618 -15279 3467 284094
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.209e+04 8.114e+03 2.723 0.00731 **
adv -1.431e+00 2.954e-01 -4.845 3.34e-06 ***
temp -1.878e+00 6.313e-01 -2.975 0.00346 **
emp -1.510e+00 7.036e-01 -2.146 0.03358 *
labor_cost 8.808e-01 1.692e-01 5.207 6.76e-07 ***
total_assets 3.516e-02 5.840e-03 6.020 1.47e-08 ***
rd 1.385e+00 5.268e-01 2.629 0.00953 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 78940 on 139 degrees of freedom
Multiple R-squared: 0.6479, Adjusted R-squared: 0.6327
F-statistic: 42.63 on 6 and 139 DF, p-value: < 2.2e-16
confint()関数を使って信頼区間を計算します。
2.5 % 97.5 %
(Intercept) 6048.51599480 3.813231e+04
adv -2.01511513 -8.470054e-01
temp -3.12602311 -6.298318e-01
emp -2.90144939 -1.190356e-01
labor_cost 0.54637427 1.215313e+00
total_assets 0.02361376 4.670793e-02
rd 0.34334525 2.426472e+00
Back to top