3  第5章 基礎統計学復習

この章で学習する確率モデルや統計的推測、統計的検定は、経営学生が非常に苦手とするところです。 なぜなら、確率的な考え方を数式で表現したり、統計的推測の抽象的な理論を理解することが難しいからです。 そこでテキストの第5章では、数学だけでなくシミュレーションを通じて、確率モデルや統計的推測、統計的検定の基本的な考え方を理解することを目指しています。 しかし、それでも難しいと感じる学生も多いと思うので、数学的な内容はできるだけスルーして、シミュレーションを通じて、確率モデルや統計的推測、統計的検定の基本的な考え方を理解するための資料になればと思います。

3.1 確率モデル、期待値と分散

テキストでは、連続型確率変数や離散型確率変数の期待値や分散の定義を解説していますが、厳密に理解したい人は、テキストの内容をしっかりと読み込んでください。 最小限の理解でいい人は、離散型確率変数の期待値と分散だけ理解しておけば十分です。

離散型確率変数とは、例えばサイコロの目のように、取りうる値が有限個である確率変数のことです。 サイコロの場合、取りうる値はX = \{ 1, 2, 3, 4, 5, 6 \}の6つであり、それぞれの値が出る確率はP(X = x_i) = 1/6です。 離散型確率変数Xの期待値E(X)は、 \begin{aligned} E(X) &= 1 \times P(X = 1) + 2 \times P(X = 2) + \cdots + 6 \times P(X = 6) \\ &= \sum_{i=1}^{6} x_i P(X = x_i) \end{aligned} で定義されます。 つまり、取りうる値x_iに対して、その値が出る確率P(X = x_i)を掛けて、すべての値について足し合わせたものが期待値になります。 また、離散型確率変数Xの分散Var(X)は、 \begin{aligned} Var(X) &= E((X - E(X))^2) \\ &= \sum_{i} (x_i - E(X))^2 P(X = x_i) \end{aligned} で定義されます。

3.2 Rでシミュレーション入門

経営学部の1回生がおおよそ学んでいるであろう統計学の内容を、Rコードとともに復習します。 テキストの内容に加えて、コードの効率化や関数化についても解説します。

最初に、本章で使うパッケージを読み込んでおきます。

# コード5-1
pacman::p_load(
  tidyverse, # データ操作の総合パッケージ集
  readxl, # Excelファイルの読み込み
  pwr,  # 効果量と検出力の計算
  ggthemes, # グラフの拡張
  knitr # 表形式での出力
)

次に、確率変数のシミュレーションを通じて、統計学の復習をしてみましょう。 まずサイコロを作ります。 ここでサイコロは、1〜6の目をもち、投げると6分の1の確率で、いずれかの目が出るもの、とします。 サイコロを振った時に出る目の期待値は、 \begin{aligned} E(X) & = \frac{1}{6} + \frac{2}{6} + \frac{3}{6} + \frac{4}{6} + \frac{5}{6} + \frac{6}{6} \\ % & = \frac{1}{6} \times (1 + 2 + 3 + 4 + 5 + 6) \\ & = \frac{21}{6} \\ & = 3.5 \end{aligned}

ですよね。 本当かどうか確かめてみます。

1から6の数値からなるベクトルdiceを作ります。

サイコロの作成

dice <- 1:6

つぎにsample()関数を用いて、diceの中から1つの数をランダムに取り出します。 ランダムさを再現するために、set.seed()関数を使って乱数のシード値を設定しておきましょう。

sample()関数の引数は以下の通りです。

• x: 抽出元のベクトル
• size: 抽出する数
• replace: 置換を許可するかどうか

サイコロを振る

set.seed(442) # 乱数のタネを設定
d <- sample(dice, size = 1) # サイコロを振る
print(d) # 結果の表示

[1] 6

結果は6となりました。

これでサイコロを振って、その結果を返すコードができました。 次に、5回サイコロを振って、その結果を出力するコードを書いてみましょう。 愚直に書くと、次のようになります。

d1 <- sample(dice, size = 1)
d2 <- sample(dice, size = 1)
d3 <- sample(dice, size = 1)
d4 <- sample(dice, size = 1)
d5 <- sample(dice, size = 1)
print(c(d1, d2, d3, d4, d5))

[1] 1 4 1 1 6

これで5回サイコロを振った結果が表示されます。 出た目の平均を計算してみると、2.6となりました。 3.5ではないですね。

もっとたくさんサイコロを振ってみようとおもいます。 プログラミングでは、同じコードを3回以上書いているなと思ったら、ループ処理や関数化を検討しましょう。 ループ処理や関数を使うことで、コードが短く、読みやすく、管理しやすいものになります。 そこで、forループを使った方法を学習しましょう。

3.2.1 forループ

forループを使って、繰り返し処理を行います。 forループの書き方は、

for (変数 in ベクトル) {
  繰り返し処理
}

と書くことで、ベクトルの要素を順番に変数に代入しながら、繰り返し処理を行うことができます。 先ほどのコードをよく見ると、変化しているのは変数名だけで、処理内容は同じであることがわかります。 そこで、変数名の数字を変数にして、ループ処理を行うと、次のようになります。

set.seed(442) # 乱数のタネを設定
n <- 10 # サイコロを振る回数
d <- numeric(n) # 空の数列を作成
for (i in 1:n) { # ループ処理
  d[i] <- sample(dice, size = 1)
}
print(d) # 結果の表示

 [1] 6 1 4 1 1 6 1 4 5 4

上のようにforループを使うと、サイコロを振る回数nを変更するだけで、コード全体を変更する必要がなくなります。

mean(d)

[1] 3.3

10回サイコロを振った結果の平均は、3.3となりました。かなり3.5に近い値になっていますね。

sample()関数は、オプションでnを指定すると、n回の抽出を行うことができるので、

d <- sample(
    dice, 
    size = 5
  )
print(d)

[1] 4 2 6 1 3

とすることで、サイコロを5回振った結果が得られるように見えますが、sample()関数はデフォルトで、非復元抽出を行うため、一旦出た要素はもう出なくなります。したがって、 上のコードだと1〜6の数値から5つをランダムに選んでいるだけになります。 そこで、replace = TRUEオプションを付けると、復元抽出となり、一旦出た要素が再び出る可能性があるようになります。

d <- sample(
    dice, 
    size = 5, 
    replace = TRUE
  )
print(d)

[1] 5 6 2 4 5

sample()関数を使って、上の繰り返し処理を使わずに、サイコロを10回振ることもできます。

d1 <- sample(dice, size = 10, replace = TRUE)
mean(d1)

[1] 4.3

サイコロを10回振って平均を計算する、という試行を3回繰り返すため、forループを使って次のように書きます。 ここでは、1回の試行でサイコロを10回振った結果として、10個の数値が入ったベクトルを得ることになり、その試行を3回繰り返すので、3つのベクトルを収納する場所をlistとして用意しておきます。

プログラミングにはおおよそlistと呼ばれる複数のオブジェクトを収納するためのデータ構造が用意されていることが多いです。 Rでは、list()関数を使って空のリストを作成し、[[i]]のようにして、リストのi番目の要素にアクセスすることができます。

d <- list() # 空のリストを作成
for (i in 1:3) { # ループ処理
  d[[i]] <- sample(dice, size = 10, replace = TRUE)
}
d # 結果の表示

[[1]]
 [1] 1 4 4 3 2 6 3 5 2 6

[[2]]
 [1] 5 3 2 6 6 5 4 6 4 3

[[3]]
 [1] 1 6 1 1 5 2 1 4 5 2

これで3つの要素(数値ベクトル)をもつリストdができました。 このリストの各要素にアクセスするには、d[[1]]、d[[2]]、d[[3]]のようにします。

これをさらに発展させて、後で変更する可能性のある変数である試行回数やサイコロを振る回数を別に設定しておいて、コードを読みやすく、また変更しやすくします。

trial_count <- 3 # 試行回数
sample_sizes <- 10 # サイコロを振る回数

# 空の数列を作成
d_mean <- numeric(trial_count) 
for (i in 1:trial_count) {
  d_mean[i] <- mean(sample(dice, size = sample_sizes, replace = TRUE))
}
d_mean

[1] 2.8 3.7 3.7

これで、trial_countとsample_sizesを変更するだけで、サイコロを振る回数や、試行回数を簡単に変更できるようになりました。

次に、試行回数trial_countとサイコロを振る回数sample_sizesを引数にした関数を作成すると、さらに便利になります。 ここでは、自作関数dice_mean()を定義してみましょう。 自作関数dice_mean()は引数として、

• trial_count: 試行回数
• sample_sizes: サイコロを振る回数

を受け取るようにします。 デフォルト値として、試行回数を3回、サイコロを振る回数を10回に設定しています。

dice_mean <- function(
  trial_count = 3,  # 試行回数 デフォルトで3回
  sample_sizes = 10 # サイコロを振る回数 デフォルトで10回
  ) {
  d_mean <- numeric(trial_count) # 空の数列を作成
  for (i in 1:trial_count) {
    d_mean[i] <- mean(sample(dice, size = sample_sizes, replace = TRUE))
  }
  return(d_mean)
}

この自作関数dice_mean()を使うと、試行回数やサイコロを振る回数を簡単に変更して、平均値を計算することができます。

dice_mean() # デフォルト値で実行

[1] 3.8 2.5 4.0

dice_mean(trial_count = 5, sample_sizes = 20) # 引数を指定して実行

[1] 3.25 3.45 3.80 3.55 3.10

dice_mean(5, 20) # 省略形でもOK

[1] 3.70 4.55 2.75 3.50 3.05

この関数を使って、サイコロを10回、100回、1,000回振ったときの平均をそれぞれ3回ずつ試行してみましょう。

set.seed(352)
size = c(10, 100, 1000)
d_mean <- list()

for (i in seq_along(size)) {
  d_mean[[i]] <- dice_mean(trial_count = 3, sample_sizes = size[i])
}

d_mean_mat <- do.call(rbind, d_mean)

# 列名を付与
colnames(d_mean_mat) <- paste0("試行", 1:ncol(d_mean_mat))
# 行名を付与
rownames(d_mean_mat) <- paste0("サイコロを", size, "回振る")
# 表として出力
knitr::kable(
  d_mean_mat,
  caption = "サイコロの標本平均（各サイズ3回ずつ）",
  align = "ccc"
)

サイコロの標本平均（各サイズ3回ずつ）

	試行1	試行2	試行3
サイコロを10回振る	3.200	3.000	2.400
サイコロを100回振る	3.440	3.340	3.560
サイコロを1000回振る	3.433	3.446	3.554

3.2.2 purrrパッケージ

forループによる繰り返し処理は処理速度に問題があるため、 より高速かつ便利なtidyverseのpurrrパッケージを使って、さらに簡潔に書きます。

set.seed(352)
trial_count <- 3 # 試行回数
sizes <- c(10, 100, 1000) # サイコロを振る回数

# map_dfr()でデータフレームを直接作成
d_mean_df <- map_dfr(sizes, function(n) {
  # replicate()で3回繰り返し試行
  results <- replicate(
    trial_count, 
    mean(sample(dice, size = n, replace = TRUE))
    )
  set_names(results, paste0("試行", 1:trial_count))
  })

result <- d_mean_df |> 
  mutate(条件 = paste0("サイコロを", sizes, "回振る")) |> 
  relocate(条件) # 「条件」列を一番左へ移動

# 出力
kable(
  result,
  caption = "サイコロの標本平均（各サイズ3回ずつ）",
  align = "cccc"
)

サイコロの標本平均（各サイズ3回ずつ）

条件	試行1	試行2	試行3
サイコロを10回振る	3.200	3.000	2.400
サイコロを100回振る	3.440	3.340	3.560
サイコロを1000回振る	3.433	3.446	3.554

サイコロを振る回数を増やしていくと、サイコロを振って出た目の平均値がどうなっていくのか、グラフにしてみましょう。

# 試行回数ベクトルの作成
n_sequence <- c(
  seq(1, 100, by = 1),
  seq(101, 1001, by = 10),
  seq(1002, 100002, by = 100)
)

# シミュレーションの実行
# 各nに対してサイコロの標本平均を1回ずつ計算します
dice <- 1:6
set.seed(352)

simulation_data <- map_dfr(n_sequence, function(n) {
  tibble(
    n = n,
    mean = mean(sample(dice, size = n, replace = TRUE))
  )
})

ggplot(simulation_data, aes(x = n, y = mean)) +
  geom_line(color = "darkblue", alpha = 0.5) +
  geom_hline(yintercept = 3.5, linetype = "dashed", color = "firebrick") +
  scale_x_log10(labels = scales::label_number()) + # 対数スケールで表示
  labs(
    title = "試行回数の増大に伴う標本平均の収束過程",
    subtitle = "横軸は対数スケール。試行回数が増えるほど3.5へ収束する様子が示されます",
    x = "試行回数 (対数スケール)",
    y = "標本平均"
  ) +
  theme_minimal()

サイコロを振った回数を多くしていくと、平均値が3.5に近づいていく様子が見えるます。 このように、サイコロを振る回数が増えると、平均値が期待値に近づいていく特性を、大数の法則と呼びます。

3.3 区間推定

いま、標準正規分布に従う母集団から抽出した無作為標本Z_1, Z_2, ..., Z_nを考えます。 標準正規分布の累積分布関数\Phi(z)を用いると、次のように表せます。

P \left( -z_{\frac{\alpha}{2}} \leq \frac{\bar{Z} - \mu}{\frac{\sigma}{\sqrt{n}}} \leq z_{\frac{\alpha}{2}} \right) = 1 - \alpha

3.4 電球の寿命データで区間推定

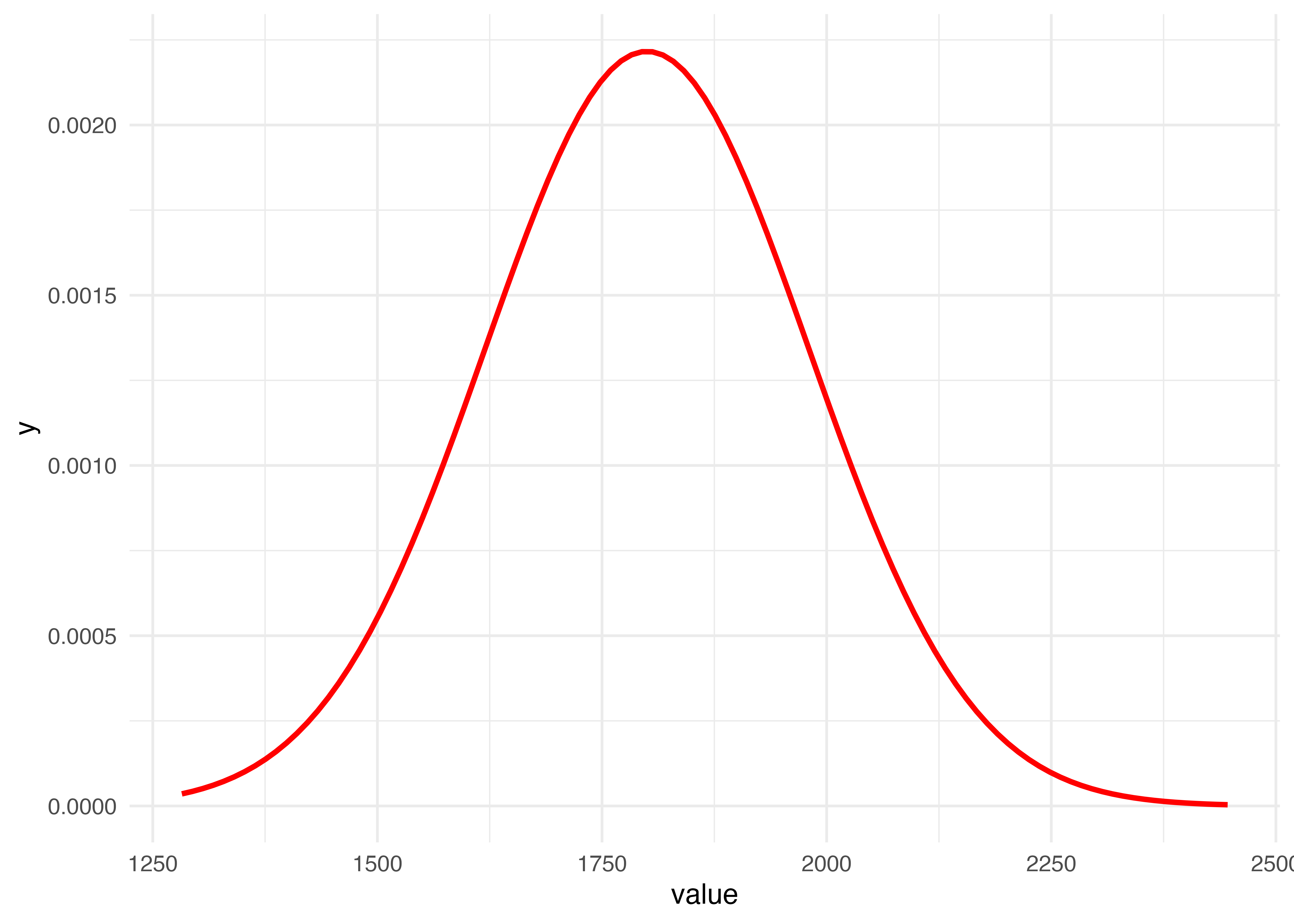
例として、次のような白熱電球の寿命データが手元にあるものとしましょう。 ここで、以下のことが分かっているものとします。

• 母平均\mu = 1800時間である。
• 母標準偏差\sigma = 180時間は既知とする。
• 個体の寿命Xは正規分布N(\mu, \sigma^2)に従う。

この設定に従うデータを生成します。 rnorm()関数を使って、1000個のデータを生成し、lifetime_sampleに格納します。

母集団の生成

average_life <- 1800 # 平均寿命
standard_dev <- 180 # 標準偏差
lifetime_sample <- tibble(
  lifetime = rnorm( # 正規分布
    1000, # データ数
    mean = average_life, # 平均
    sd = standard_dev # 標準偏差
  )
)

この1000個のデータをヒストグラムに表してみます。 理論上の正規分布の確率密度関数を赤線で表します。

lifetime_sample |>
  ggplot(aes(x = lifetime)) +
  geom_histogram(
    aes(y = after_stat(density)),
    bins = 30,
    fill = "lightblue",
    color = "black",
    alpha = 0.7
    ) +
  stat_function(
    fun = dnorm,
    args = list(mean = average_life, sd = standard_dev),
    color = "red",
    linewidth = 1
    ) +
  theme_economist_white()

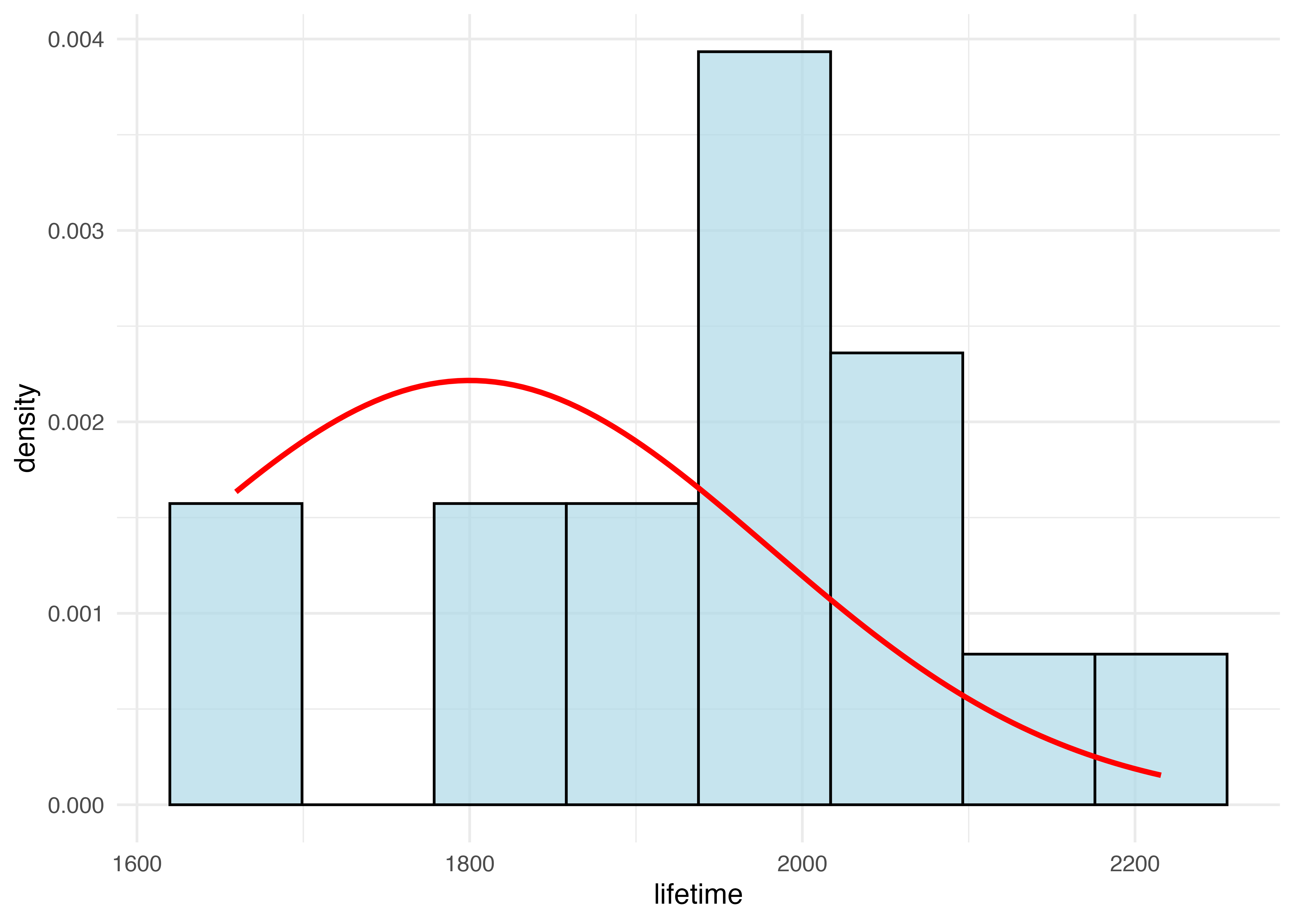
この分布から抽出したと想定される16個の電球の寿命データが以下の通りです。

# コード5-5
bulb <- c(# 白熱電球の寿命データ
    1939.6, 1680.3, 1982.1, 2215.6,
    2092.5, 1928.9, 2003.8, 1955.5,
    1800.1, 1659.5, 2066.2, 2107.2,
    2085.5, 1878.6, 2007.6, 1816.1
  )

この1つの標本(sample)の平均と標準偏差は以下のようになります。

(m_bulb <- mean(bulb))

[1] 1951.194

(sd_bulb <- sd(bulb))

[1] 154.4567

理論上の正規分布に、この標本のデータのヒストグラムを重ねると、次のようになります。

# ヒストグラムの作成
bulb_df <- tibble(lifetime = bulb)
bulb_df |> 
  ggplot(aes(x = lifetime)) +
  geom_histogram(
    aes(y = ..density..),
    bins = 8,
    fill = "lightblue",
    color = "black",
    alpha = 0.7
    ) +
  geom_vline(xintercept = m_bulb, colour="blue", linetype = "dashed") +
  geom_vline(xintercept = 1800, colour = "red", linetype = "dashed") +
  stat_function(
    fun = dnorm,
      args = list(
        mean = average_life, 
        sd = standard_dev
      ),
    color = "red",
    linewidth = 1
    ) +
  xlim(1200, 2400) + 
  theme_economist_white()

平均1800、標準偏差180の正規分布にしたがう母集団から取り出した16個のデータからなる標本の平均は、1800ではなく、1951.19375となっています。 この手元にある16個の電球の寿命データの平均値が、母平均1800の周りでどの範囲に入るかを95％信頼区間で推定してみましょう。

この節では、仮定に応じて次の2通りを明確に分けます。

• 母標準偏差\sigmaが既知: zに基づく区間推定
• 母標準偏差\sigmaが未知: tに基づく区間推定

まず、この章の設定（\sigma = 180既知）に対応するz区間を計算します。

n <- length(bulb) # 標本サイズ
z <- qnorm(0.025, lower.tail = FALSE) # 上側2.5%点
xbar <- mean(bulb) # 標本平均
sigma <- 180 # 母標準偏差（既知）

upper <- xbar + z * (sigma / sqrt(n))
lower <- xbar - z * (sigma / sqrt(n))

ci.bulb <- matrix(c(lower, upper), nrow = 1)
colnames(ci.bulb) <- c("ci.lower", "ci.upper")
knitr::kable(
  ci.bulb,
  caption = "Bulb data CI (95%, sigma known)",
  align = "cc"
)

Bulb data CI (95%, sigma known)

ci.lower	ci.upper
1862.995	2039.392

比較のため、実務でよくある「\sigma未知」の場合として、t.test()によるt区間も計算します。

bulb_ci_t <- t.test(bulb, conf.level = 0.95)
bulb_ci_t$conf.int

[1] 1868.890 2033.498
attr(,"conf.level")
[1] 0.95

実際にどの程度の平均値が信頼区間になるのかシミュレーションで確認してみましょう。

平均1800、標準偏差180の正規分布から、標本サイズ16の標本を1000回発生させ、標本平均を1000個計算してヒストグラムにしてみます。

標本平均のシミュレーション

# サンプルを1000個作成
set.seed(442)
trials <- 1000
n <- 16

# 正規母集団 N(1800, 180^2) から直接サンプリング
samples <- matrix(
  rnorm(trials * n, mean = average_life, sd = standard_dev),
  nrow = trials,
  ncol = n
)
d_mean <- rowMeans(samples)
summary(d_mean)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1681    1772    1801    1802    1829    1922 

この標本サイズ16の標本1000個から計算した1000個の平均値のヒストグラムを書きます。

標本平均のヒストグラム

df_mean <- tibble(d_mean)
ggplot(df_mean) + 
  aes(x = d_mean) + 
  geom_histogram(
    bins = 30,
    fill = "lightblue",
    color = "black",
    alpha = 0.7
  ) + 
  theme_economist_white()

これが平均1800の正規母集団から得た1000個の標本平均の分布です。この標本平均の平均を計算してみます。

標本平均の平均

d_mean_mean <- d_mean |> mean()
d_mean_mean

[1] 1801.999

母集団から取り出した1000個の標本の標本平均の平均は、1801.9993428となり、母平均1800に近い値になっています。

では100万個の標本から平均値を計算して、その平均値を計算してみます。

大量の標本平均のシミュレーション

set.seed(442)
trials <- 1000000
n <- 16
samples <- matrix(
  rnorm(trials * n, mean = average_life, sd = standard_dev),
  nrow = trials,
  ncol = n
)
d_mean <- rowMeans(samples)

大量の標本平均のヒストグラム

df_mean <- tibble(d_mean)
ggplot(df_mean) + 
  aes(x = d_mean) + 
  geom_histogram(
    bins = 30,
    fill = "lightblue",
    color = "black",
    alpha = 0.7
  ) + 
  theme_economist_white()

この100万個の標本の平均の平均を見てみると、母集団の1800に近づいていることが分かります。

大量の標本平均の平均

d_mean_mean2 <- d_mean |> mean()
d_mean_mean2

[1] 1799.986

試行回数を増やすことで、標本平均の平均が母平均に近づく特性を、大数の法則と呼びます。 また、標本平均\bar{X}自体のばらつきは標準誤差\sigma / \sqrt{n}で決まり、この例では180 / \sqrt{16} = 45です。

# 参考: z区間で使う標準正規分布の上側2.5%点
qnorm(0.025, lower.tail = FALSE)

[1] 1.959964

# 再掲: 母標準偏差既知（sigma=180）での95% z区間
n <- length(bulb)
z <- qnorm(0.025, lower.tail = FALSE)
xbar <- mean(bulb)
sigma <- 180

upper <- xbar + z * (sigma / sqrt(n))
lower <- xbar - z * (sigma / sqrt(n))

ci.bulb <- matrix(c(lower, upper), nrow = 1)
colnames(ci.bulb) <- c("ci.lower", "ci.upper")
knitr::kable(
  ci.bulb,
  caption = "Bulb data CI (95%, sigma known)",
  align = "cc"
)

Bulb data CI (95%, sigma known)

ci.lower	ci.upper
1862.995	2039.392

# コード5-8
mean(bulb)

[1] 1951.194

# コード5-9
t.test(bulb, alternative = "two.sided", mu = 1800)

    One Sample t-test

data:  bulb
t = 3.9155, df = 15, p-value = 0.001377
alternative hypothesis: true mean is not equal to 1800
95 percent confidence interval:
 1868.890 2033.498
sample estimates:
mean of x 
 1951.194 

# コード5-10
n <- length(bulb) # 標本サイズの計算
z <- qnorm(0.025, lower.tail = FALSE) # 上側2.5％点の分位点
xbar <- mean(bulb) # 標本平均の計算
sigma <- 180 # 母標準偏差の設定
mu <- 1800 # 帰無仮説の平均値 
# Z値の計算
Z <- (xbar - mu) / (sigma / sqrt(n))
Z

[1] 3.359861

データの読み込みと前処理

firmdata <- readxl::read_xlsx("data/MktRes_firmdata.xlsx")
firm2018 <- firmdata |>
  filter(fyear == 2018) |> # 2018に限定
  mutate( # ダミー変数を作成
    ad_dummy = ifelse(adint > median(adint), 1, 0)
    )
# t検定の実施
t.test(sales ~ ad_dummy, data = firm2018)

    Welch Two Sample t-test

data:  sales by ad_dummy
t = -3.3989, df = 85.686, p-value = 0.001029
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
 -1674283.1  -438496.1
sample estimates:
mean in group 0 mean in group 1 
       725009.7       1781399.3 

# コード5-12
var.test(sales ~ ad_dummy, data = firm2018, ratio = 1)

    F test to compare two variances

data:  sales by ad_dummy
F = 0.10863, num df = 74, denom df = 71, p-value < 2.2e-16
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.06821636 0.17258882
sample estimates:
ratio of variances 
         0.1086276 

# 効果量d=0.8、検出力0.8、有意水準0.05の場合の
# 必要標本サイズの推定
est_n <- pwr.t.test(d = 0.8, power = 0.8, sig.level = 0.05)
est_n

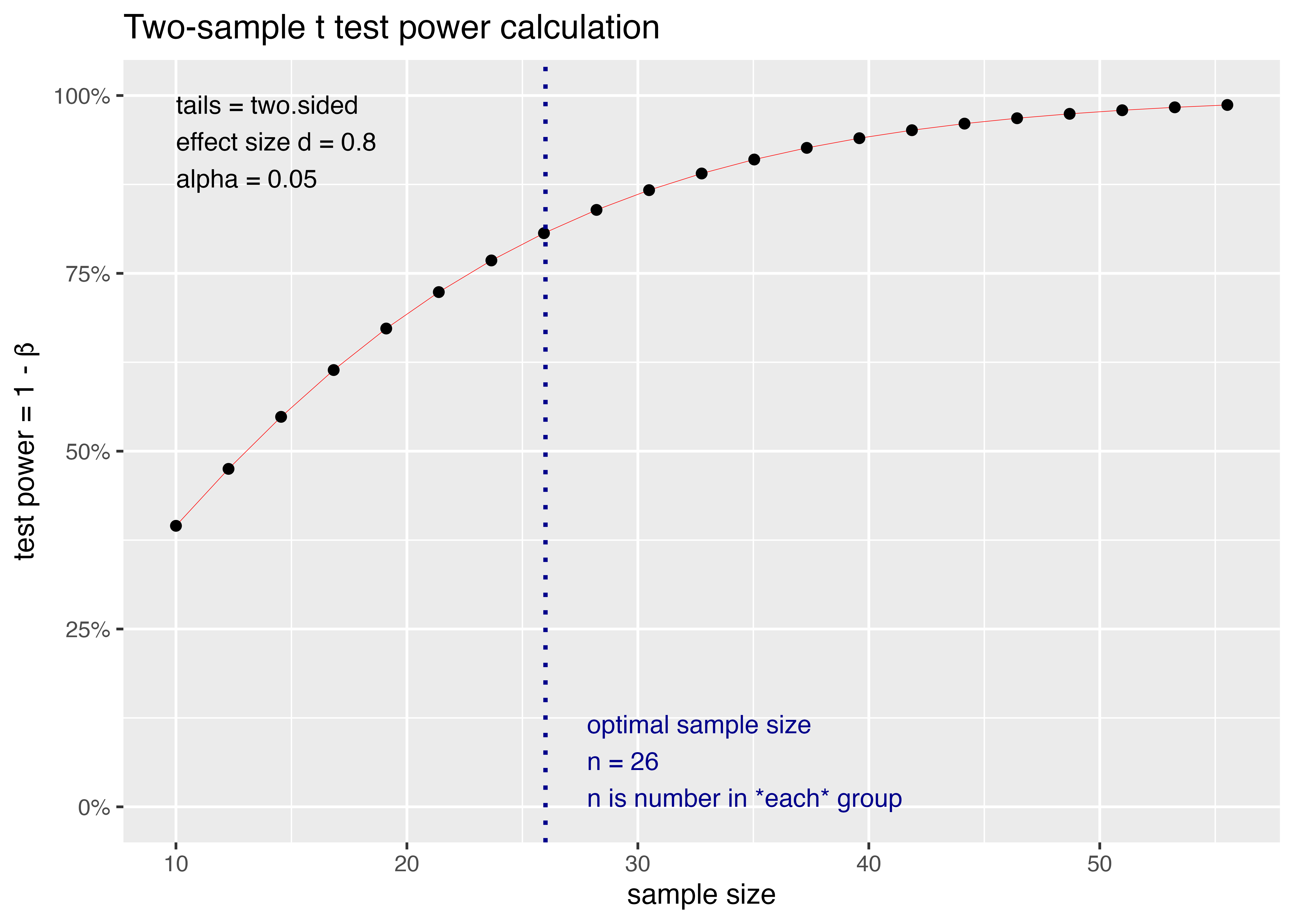
     Two-sample t test power calculation 

              n = 25.52458
              d = 0.8
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

# コード5-15
plot(est_n)

# コード5-16
pwr.t.test(d = 0.8, n = 26, sig.level = 0.05)

     Two-sample t test power calculation 

              n = 26
              d = 0.8
      sig.level = 0.05
          power = 0.8074866
    alternative = two.sided

NOTE: n is number in *each* group