因子分析 (factor analysis)は,心理尺度などを用いる質問紙を用いた研究・調査を行う場合は必須の分析手法です。 今回に限り,テキスト「行動科学の統計学」ではなく,因子分析についての記述が丁寧な南風原 (2002)『心理統計学の基礎 』有斐閣を参考にしています。
あるいは松尾・中村 (2002)『誰も教えてくれなかった因子分析』北大路書房もオススメです。
因子分析の考え方
200名の大学生に対して、8つの性格特性を7件法で尋ねています。
温和
陽気
外交的
親切
社交的
協力的
積極的
素直
すべてポジティブな用語で、意味が似ているものもあるようにみえます。 そこでより少数の変数で特性を測れないか ,について考えてみます。
RQ : 1つの特性にあてはまる人は,他のすべてにもあてはまる傾向があるのでは?あるいは,いくつかの特性群に分類することができるのでは?
この8つの特性を分類することで,個人の特性をより少数の変数で把握することができるのではないかと考えます。 情報量を減らさずに分析で利用する変数の数を減らすことができれば ,分析が容易になります。 たとえば,回帰分析で回帰式に8個の特性をすべて入れ込むと,多重共線性もあり,好ましくない可能性があります。 そこで因子分析では,複数の変数の共通因子を特定するこで,次元を落とすことを目的 としている。
例えば,パーソナル心理学で有名なBIG5 では,個人の性格を5つで代表できる,と主張している。
テキストに記載されている性格特性の相関係数を見てみると,外交的と社交的,積極的と外交的,積極的と社交的は高く正の相関があることがわかります。 そこで、これら8つの観測変数を,
8つの観測変数に共通する 部分
8つの観測変数に共通しない 部分
に分類することを考えます。 ここでは,因子分析により複数(3項目以上)の連続変数 の観測変数の共通する部分を抽出してみます。
因子分析モデル
因子分析の1因子モデル (one-factor model)は,観測変数が1つの共通因子によって説明されると考えるモデルです。 1因子モデルを数式で表すと,
\text{温和} = \beta _1 \times f + \varepsilon_1\\
\text{陽気} = \beta _2 \times f + \varepsilon_2\\
\vdots\\
\text{素直} = \beta _8 \times f + \varepsilon_8\\
となります。 ここで \beta は因子負荷 (factor loading,あるいは因子スコア),f は共通因子 (common factor),\varepsilon は独自因子 (unique factor)を表しています。 共通因子は,観測変数に共通する部分を表し,独自因子は観測変数に特有の部分を表します。因子負荷は,観測変数と共通因子の関係を表す係数です。
m因子モデル
8個の個人特性の背後に2つの共通因子f_1 とf_2 があると考える場合,因子モデルは次のように表すことができます。
\text{温和} = \beta _{11} \times f_1 + \beta _{12} \times f_2 + \varepsilon_1\\
\text{陽気} = \beta _{21} \times f_2 + \beta _{22} \times f_2 + \varepsilon_2\\
\vdots\\
\text{素直} = \beta _{81} \times f_8 + \beta _{82} \times f_2 + \varepsilon_8\\
一般的に,p 個の観測変数(アンケート項目)に対して,m 個の共通因子によって説明されるとする因子モデルは,
\begin{align}
y_j &= \beta_{j1} f_1 + \beta_{j2} f_2 + \cdots + \beta _{jm} f_m + \varepsilon_j\\
&=\sum _{g=1}^m \beta_{jg} f_g + \varepsilon_j, \quad (j=1,2, \dots, p)
\end{align}
となります。 「掛けて足す,掛けて足す」があるときは,行列を用いて表すことができます。
\begin{aligned}
\begin{pmatrix}
y_1\\
y_2\\
\vdots\\
y_p
\end{pmatrix}
&=
\begin{pmatrix}
\beta_{11} & \beta_{12} & \cdots & \beta_{1m}\\
\beta_{21} & \beta_{22} & \cdots & \beta_{2m}\\
\vdots & \vdots & \ddots & \vdots\\
\beta_{p1} & \beta_{p2} & \cdots & \beta_{pm}
\end{pmatrix}
\begin{pmatrix}
f_1\\
f_2\\
\vdots\\
f_m
\end{pmatrix}
+
\begin{pmatrix}
\varepsilon_1\\
\varepsilon_2\\
\vdots\\
\varepsilon_p
\end{pmatrix}
\end{aligned}
まとめて書くと,
\underbrace{\boldsymbol{y}}_{p \times 1} = \underbrace{\boldsymbol{\beta}}_{p \times m} \underbrace{\boldsymbol{f}}_{m \times 1} + \underbrace{\boldsymbol{\varepsilon}}_{p \times 1}
因子得点
抽出した因子における個人の位置を因子得点 (factor score)として保存し,分析に用いることがあります。 この因子得点がアンケートなどで集められた複数の質問項目から抽出された因子に基づく合成尺度として利用されます。
分析
いつものテキスト302頁のデータを用います。 飲み物の好みの仮想データ であり,
コーヒー(cafe),
紅茶(tea),
ミルク(milk),
水(water),
緑茶(g_tea),
ウーロン茶(w_tea),
性別(sex)
という項目から構成されています。 各項目に対する好みは,5点尺度で測定されています。 まずはデータを読み込む。
pacman :: p_load ( tidyverse , stargazer , corrplot ) df <- read_csv ( "data/chap14.csv" )
Rows: 20 Columns: 8
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (8): ID, café, tea, milk, water, g_tea, w_tea, sex
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
まずは記述統計と相関行列を確認します。
ID café tea milk water
Min. : 1.00 Min. :0.00 Min. :1.00 Min. :2.0 Min. :0.0
1st Qu.: 5.75 1st Qu.:2.00 1st Qu.:2.75 1st Qu.:3.0 1st Qu.:0.0
Median :10.50 Median :2.00 Median :3.00 Median :3.5 Median :1.5
Mean :10.50 Mean :2.45 Mean :3.10 Mean :3.5 Mean :1.3
3rd Qu.:15.25 3rd Qu.:3.00 3rd Qu.:4.00 3rd Qu.:4.0 3rd Qu.:2.0
Max. :20.00 Max. :4.00 Max. :5.00 Max. :5.0 Max. :3.0
g_tea w_tea sex
Min. :0.00 Min. :1.00 Min. :1.0
1st Qu.:1.00 1st Qu.:2.00 1st Qu.:1.0
Median :2.00 Median :2.50 Median :1.0
Mean :1.70 Mean :2.75 Mean :1.4
3rd Qu.:2.25 3rd Qu.:4.00 3rd Qu.:2.0
Max. :3.00 Max. :4.00 Max. :2.0
df |> select ( - ID ) |>
cor ( ) |>
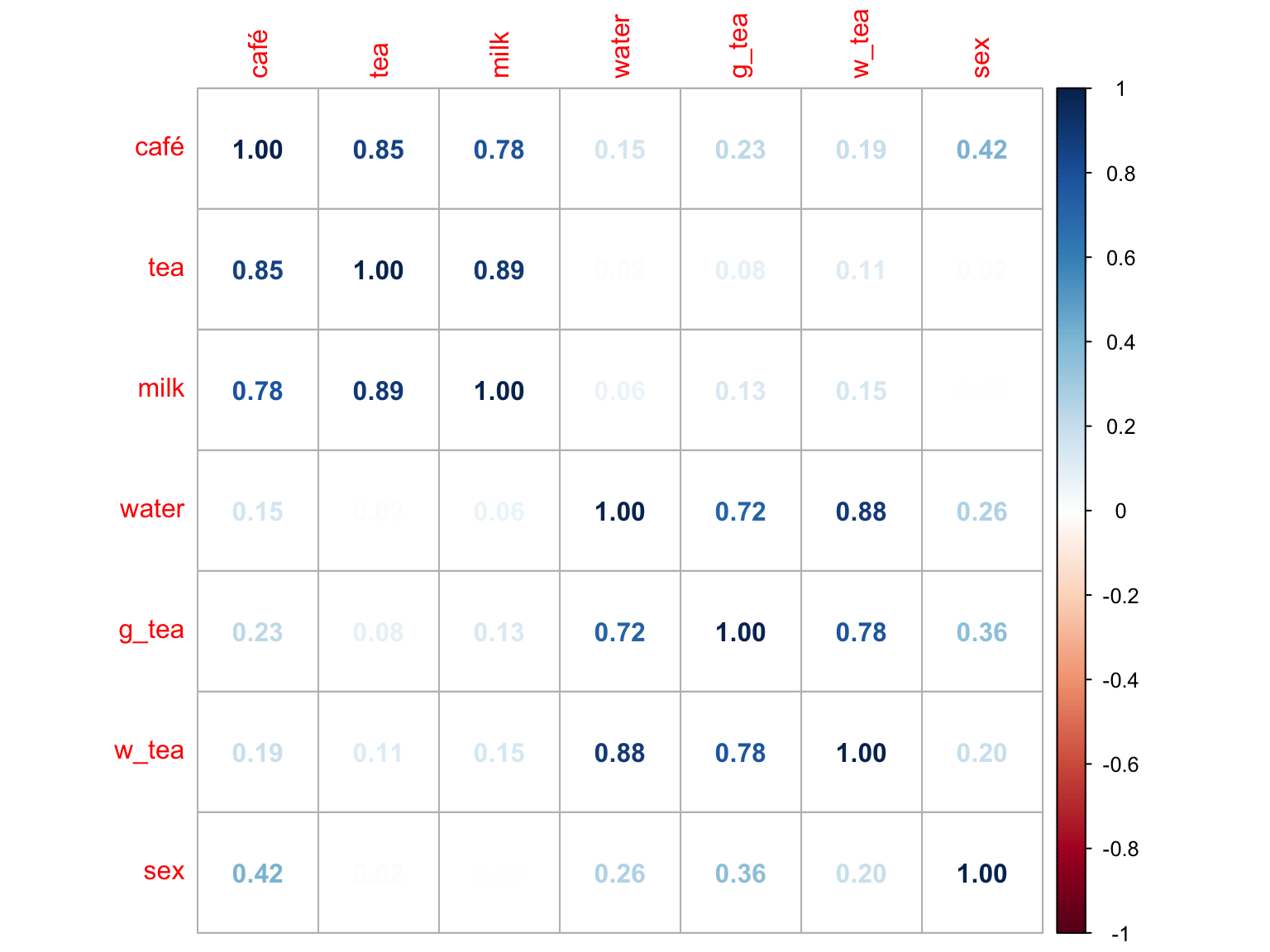
corrplot :: corrplot ( method = "number" )
相関係数行列より,コーヒーと紅茶とミルクの間の相関係数と、水と緑茶と烏龍茶の間の相関係数が高いことが分かります。
次に因子分析 (factor analysis)を行います。 因子分析は,基本関数factanal() psychのfa()関数を用います。 まずはfactanal()
factanal()
基本関数factanal() factorsを指定しないとエラーになるため,因子数を指定しなくても動くように改良されたfactanal2()を利用することもあります。
軸の回転をしないときはnone,プロマックス回転ならpromax,バリマックス回転ならvarimaxとします。 因子得点の計算方法は,デフォルトはnone,あとはregressionやBartlettがあります。詳しくはfacanal()のヘルプを参照してください。
f1 <- factanal ( # 因子分析 df [ ,2 : 7 ] , # データ
factors = 2 , # 因子数
rotation = "promax" , # 回転方法
scores = "regression" # 因子得点の計算方法
)
print ( f1 , cutoff = 0 )
Call:
factanal(x = df[, 2:7], factors = 2, scores = "regression", rotation = "promax")
Uniquenesses:
café tea milk water g_tea w_tea
0.247 0.015 0.192 0.163 0.356 0.063
Loadings:
Factor1 Factor2
café 0.855 0.069
tea 0.999 -0.056
milk 0.899 -0.001
water -0.064 0.922
g_tea 0.012 0.801
w_tea 0.026 0.964
Factor1 Factor2
SS loadings 2.544 2.429
Proportion Var 0.424 0.405
Cumulative Var 0.424 0.829
Factor Correlations:
Factor1 Factor2
Factor1 1.000 0.147
Factor2 0.147 1.000
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 1.73 on 4 degrees of freedom.
The p-value is 0.786
cutoff = 0のオプションをつけることで,すべての因子負荷を出力します。
Loadings:で因子負荷量をみると,
因子1はコーヒー・紅茶・ミルク,
因子2は水・緑茶・麦茶
の負荷量が高いことがわかります。 そこで第1因子に「味の濃い飲み物」,第2因子に「味の薄い飲み物」という名前をつけてみます 。 この因子負荷量を第1因子と第2因子の軸をもつ平面にプロットしてみます。
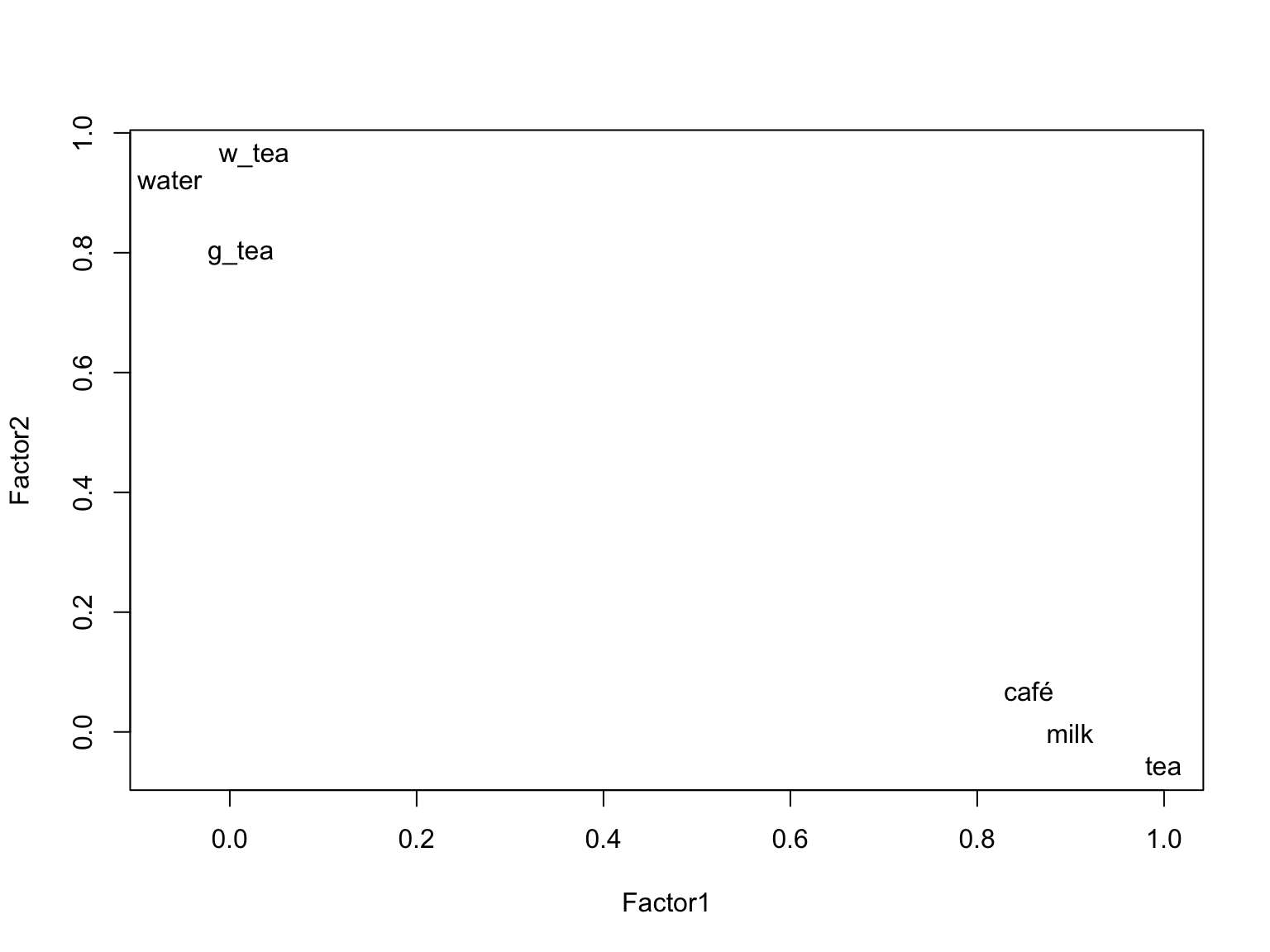
plot ( f1 $ loadings , type = "n" ) text ( f1 $ loadings , colnames ( df [ ,2 : 7 ] ) ) # 散布図の点を項目名にする
すると見た目にも、水、緑茶、烏龍茶のグループと、コーヒー、紅茶、ミルクのグループが分かれていることがわかります。
因子得点の保存
factanal() scoresというオブジェクト(行列形式)で保存されてます。 確認してみましょう。
Factor1 Factor2
[1,] -0.178523355 0.3690318
[2,] 1.015440684 -1.6155025
[3,] 0.877004772 -1.0030949
[4,] -1.131833963 1.1416150
[5,] 1.886141136 -1.1270865
[6,] -0.236835287 1.0050679
[7,] 0.807421122 1.2269626
[8,] 0.012360586 -0.7529136
[9,] -0.148168863 0.4826660
[10,] -1.101479472 1.2552492
[11,] 0.002527429 -0.7132283
[12,] -1.905266829 -0.3279822
[13,] -0.002238124 -0.9454804
[14,] 0.762593579 0.9828963
[15,] -0.081255768 -0.6121495
[16,] 0.702990932 1.1125873
[17,] 0.887818606 -0.7479554
[18,] -1.033460041 0.5173932
[19,] 0.722531589 0.9710820
[20,] -1.857768732 -1.2191579
この因子得点をもとのデータ・フレームに追加します。
df $ fac1 <- f1 $ score [ ,1 ] # 行列の1列目が第1因子 df $ fac2 <- f1 $ score [ ,2 ] # 行列の2列目が第2因子df
因子得点を追加したデータ・フレームを用いて分析を進める。 因子に男女差があるかどうかを調べてみる。
Welch Two Sample t-test
data: df$fac1 by df$sex
t = -0.057752, df = 17.892, p-value = 0.9546
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
-0.9471975 0.8965368
sample estimates:
mean in group 1 mean in group 2
-0.01013213 0.01519819
Welch Two Sample t-test
data: df$fac2 by df$sex
t = -1.0334, df = 14.195, p-value = 0.3187
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
-1.4552064 0.5080329
sample estimates:
mean in group 1 mean in group 2
-0.1894347 0.2841520
男女差は統計的に有意ではないため,両因子において男女差があるかどうかについて、何も言うことはできません。
宿題
5教科の成績情報50名分が入っているseiseki.csvファイルを読み込みます。 個人を示すID列は不要なので,削除しておきます。
df2 <- read_csv ( "data/seiseki.csv" ) |> select ( - ID ) # ID列を削除
Rows: 50 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (6): ID, 国語, 英語, 数学, 物理, 化学
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
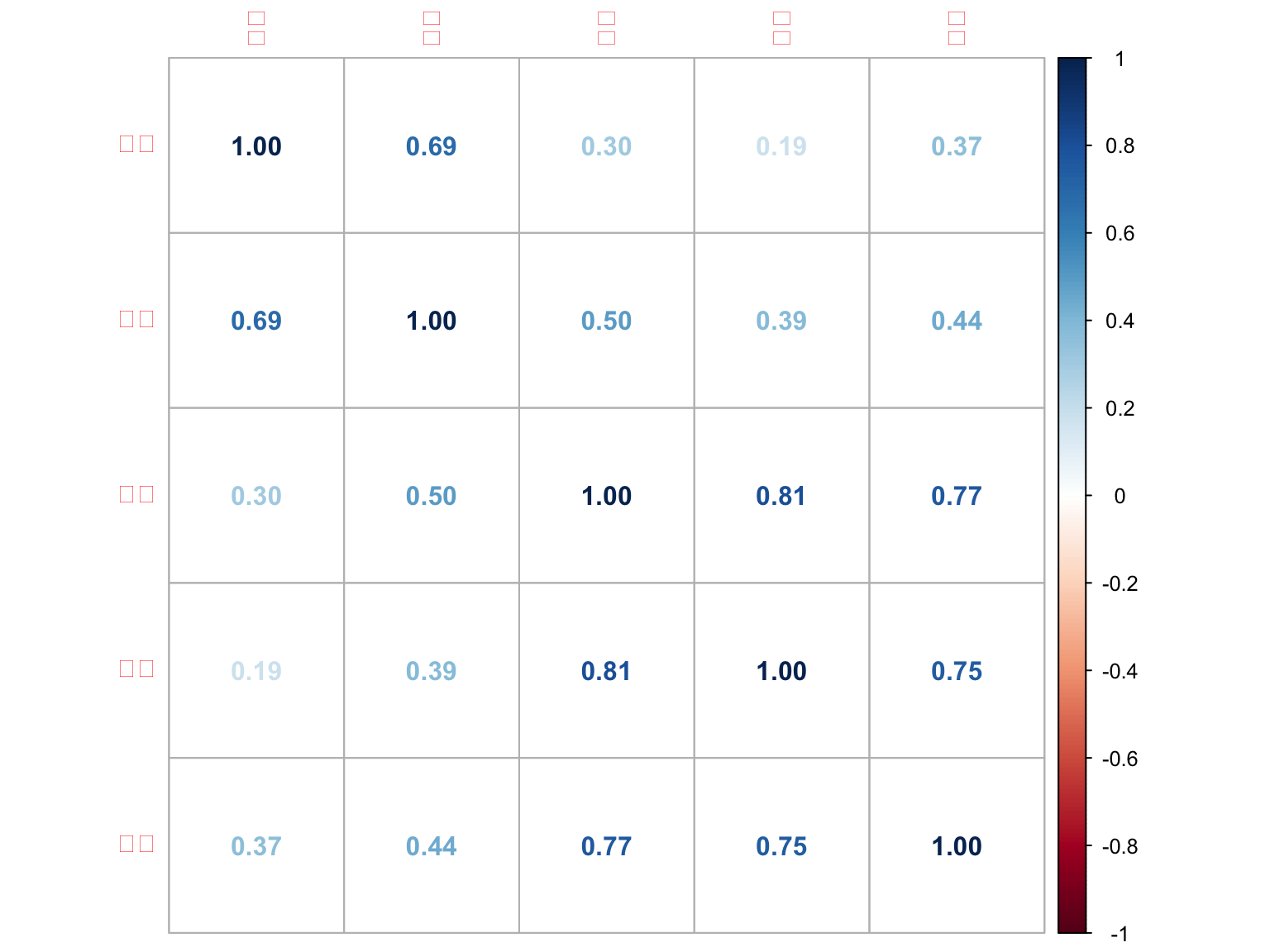
まずは変数間の相関係数を確認してみましょう。
つぎに,因子分析を行います。 事前に「文系」と「理系」という2因子が表れることを期待して,因子数は2とします。
f2 <- factanal ( df2 ,
factors = 2 ,
rotation = "promax" ,
scores = "regression"
)
print ( f2 , cutoff = 0 )
Call:
factanal(x = df2, factors = 2, scores = "regression", rotation = "promax")
Uniquenesses:
国語 英語 数学 物理 化学
0.005 0.436 0.171 0.191 0.279
Loadings:
Factor1 Factor2
国語 -0.149 1.060
英語 0.239 0.607
数学 0.923 -0.026
物理 0.964 -0.158
化学 0.806 0.084
Factor1 Factor2
SS loadings 2.509 1.524
Proportion Var 0.502 0.305
Cumulative Var 0.502 0.807
Factor Correlations:
Factor1 Factor2
Factor1 1.000 0.475
Factor2 0.475 1.000
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 1.47 on 1 degree of freedom.
The p-value is 0.225
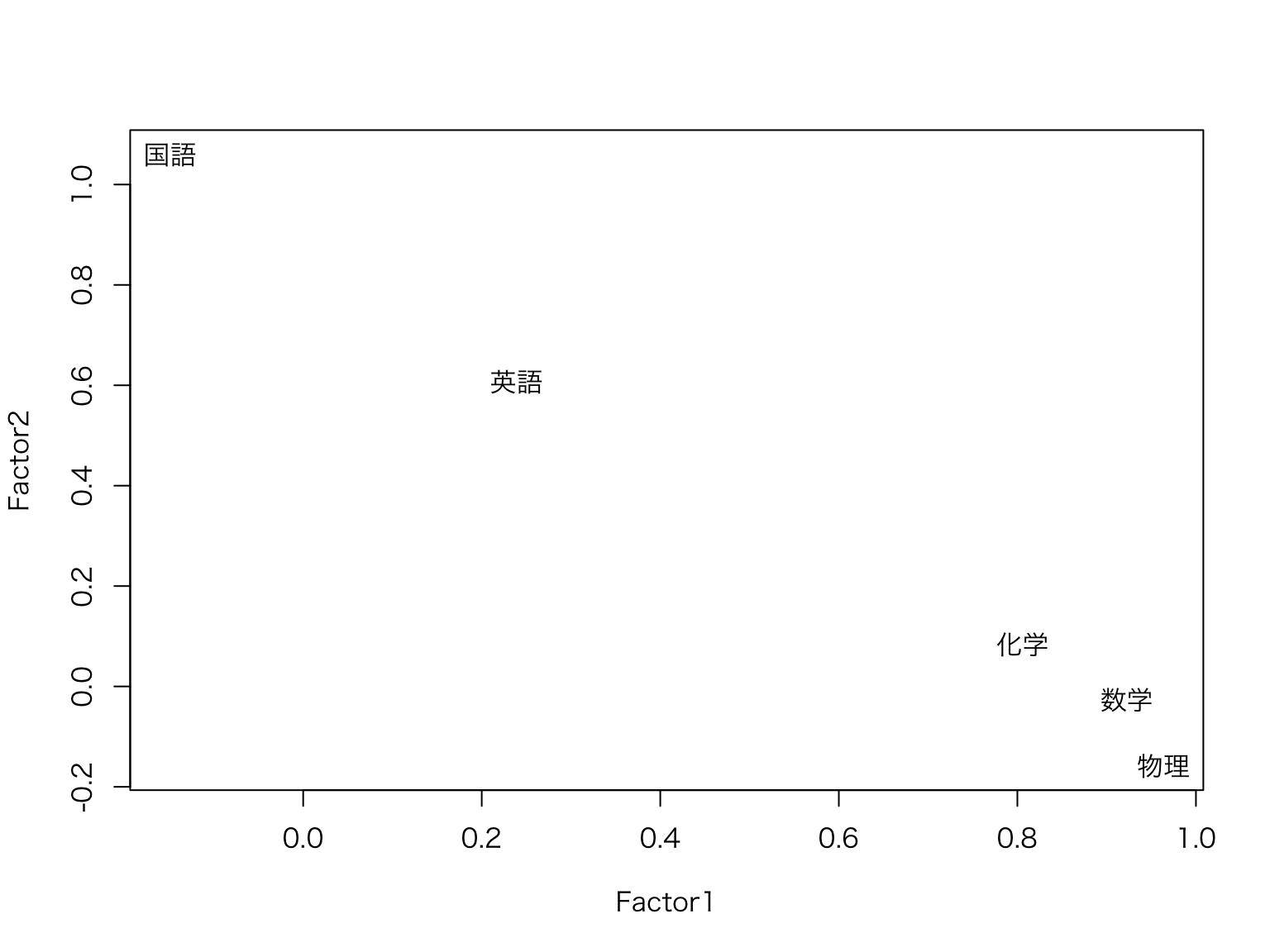
これを因子を軸とする平面に描写します。
この結果より,第1因子は数学,物理,化学を代表しており,第2因子は国語と英語を代表していると考えられます。 そこで第1因子を「理系」,第2因子を「文系」と名付けます。
psychパッケージ
psychパッケージは心理学で用いる分析手法が用意されたパッケージで,因子分析にはfa.parallel()がある。
次に,上記のデータを用いて分析を再実行する。
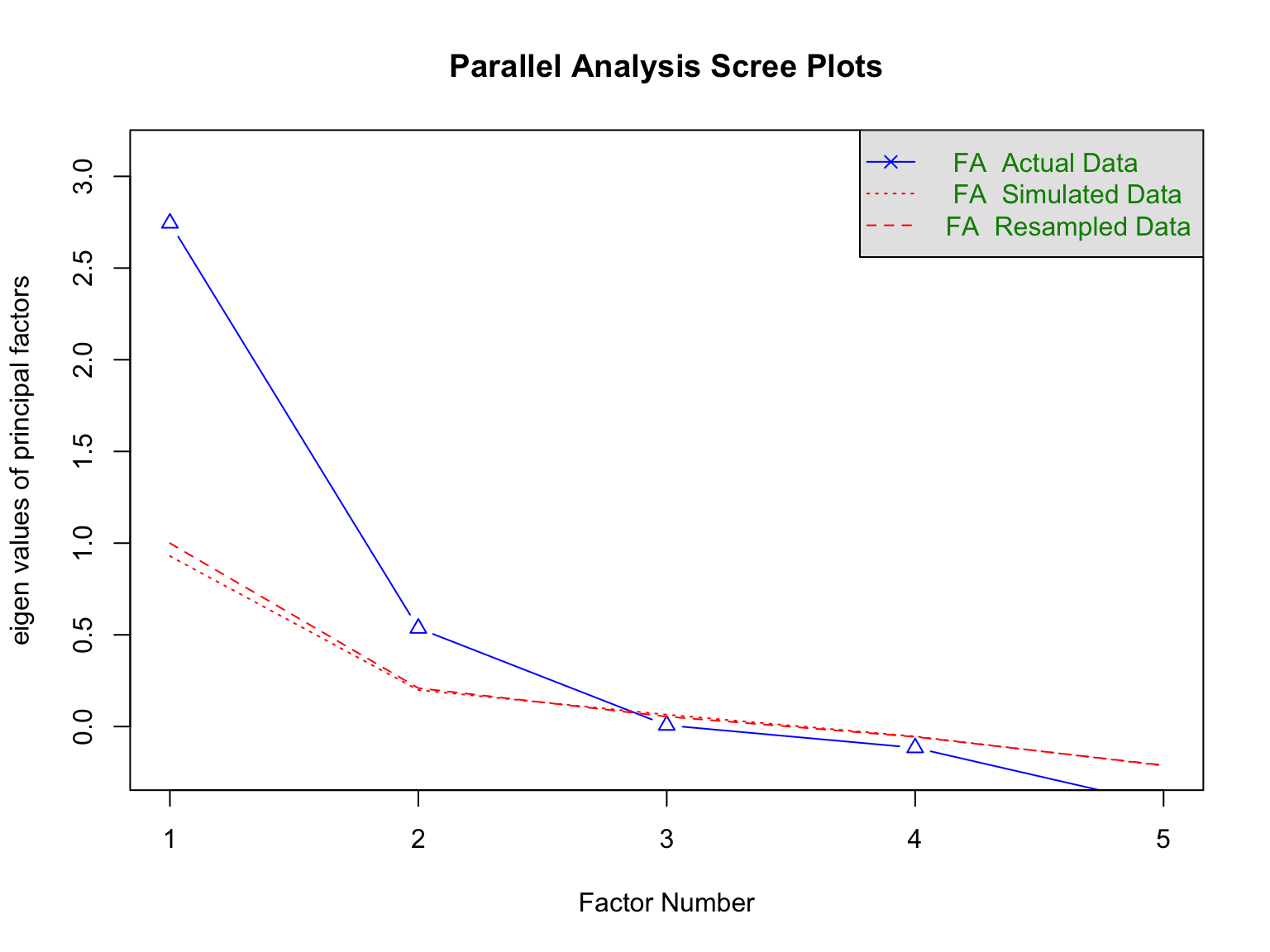
fa.parallel ( df2 , fm = "minres" , fa = "fa" , cor = "cor" )
Parallel analysis suggests that the number of factors = 2 and the number of components = NA