2種類のn個のデータY_iとX_i，i=1,\dots ,nが手元にあり，この2変数の線形関係を分析したいと考える。 回帰分析では，次のような関係を考える。
Y_i = a + b X_i + \varepsilon _i
データの関係をもっとも良く説明できる直線を推定する。つまり，パラメータaとbを決めたい，ということである。 そこで何らかのパラメータaとbの下で推定されたものを\hat Y(わいはっと)で表す。
\hat Y_i = a + b X_i
しかし，実際のデータはモデルの直線上にすべて乗っているわけではなく，誤差がある。
Y_i - \hat Y_i = \varepsilon _i
誤差の自乗和を考える。
Q = \sum _{i=1}^n \varepsilon ^2 = \sum _{i=1}^n (Y_i - a - bX_i)^2
この誤差の二乗和Qを最小にするようなパラメータaとbの求める方法が最小自乗法(Ordinaly Least Square Method)である。
\min_{a,b} Q %= \varepsilon^2 = \min_{a,b} (Y_i - (a + bX_i))^2
上記の問題をといた\hat aと\hat bが最小二乗推定値となる。
職業威信スコアがどのような要因に影響を受けているのかを考える。
pacman::p_load(tidyverse)
chap11 <- read_csv("data/chap11.csv")Rows: 20 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (5): ID, age, eduy, job_sc, f_job_sc
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.データの記述統計量を確認する。
summary(chap11) ID age eduy job_sc f_job_sc
Min. : 1.00 Min. :21.00 Min. : 9 Min. :38.10 Min. :42.00
1st Qu.: 5.75 1st Qu.:31.75 1st Qu.:12 1st Qu.:43.83 1st Qu.:45.60
Median :10.50 Median :53.50 Median :12 Median :48.55 Median :48.55
Mean :10.50 Mean :47.40 Mean :12 Mean :49.23 Mean :48.66
3rd Qu.:15.25 3rd Qu.:60.50 3rd Qu.:12 3rd Qu.:52.20 3rd Qu.:51.30
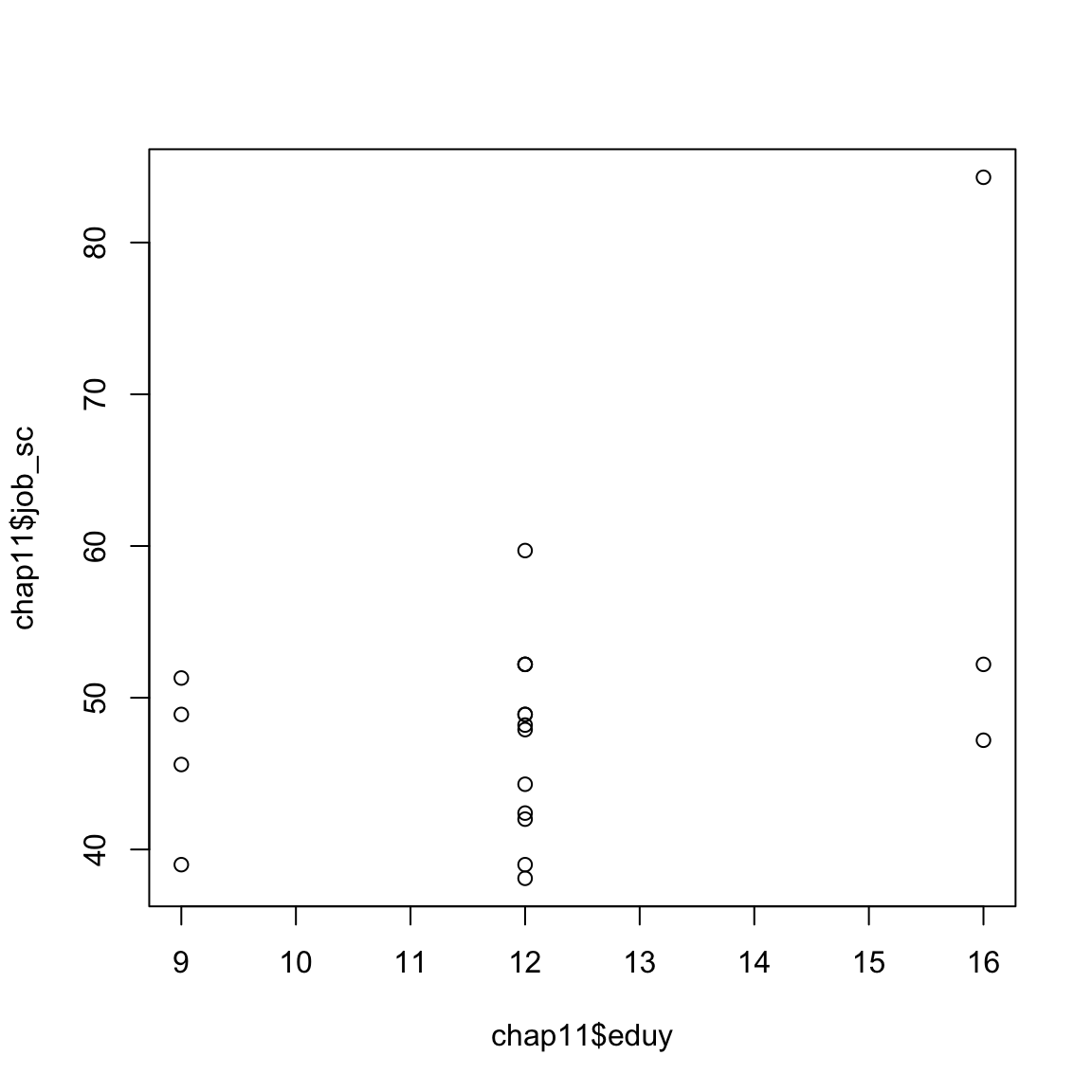
Max. :20.00 Max. :70.00 Max. :16 Max. :84.30 Max. :63.60 教育年数(eduy)と職業威信スコア(job_sc)の散布図を確認する。
plot(chap11$eduy,chap11$job_sc)
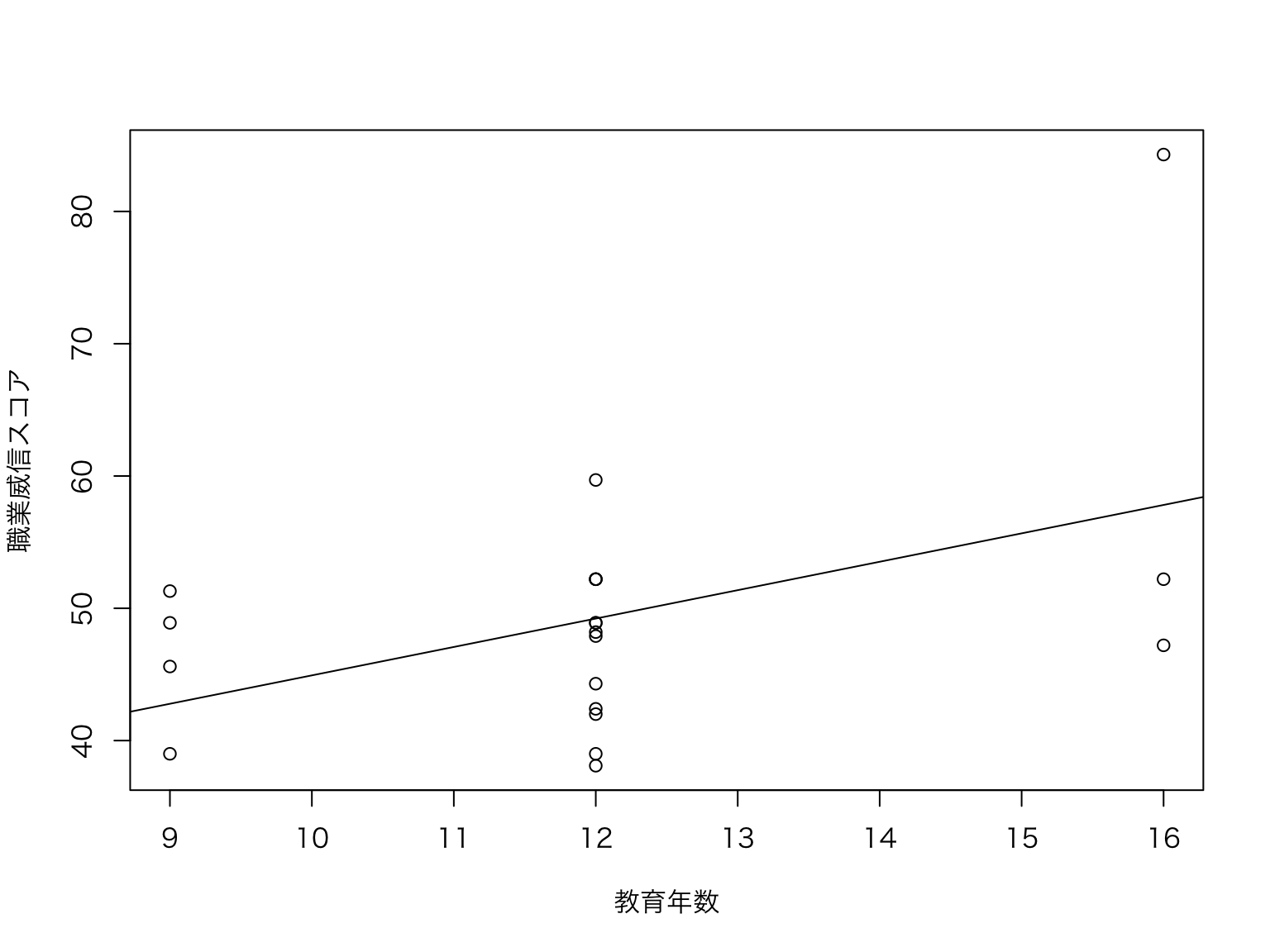
異常値の存在が懸念されるが，おおよそ右肩上がりの関係があるように見える。 散布図に直線を引くとこんな感じになる。
次に，最小自乗法による回帰分析を行う。ここでは従属変数を職業威信スコア，独立変数を教育年数とする。つまり， \text{職業威信スコア} = \alpha + \beta \times \text{教育年数} + \varepsilon
の回帰モデルを推定する。回帰モデルの推定は，lm()関数を用いる。
lm(従属変数 ~ 独立変数)のように書く。
Call:
lm(formula = job_sc ~ eduy, data = chap11)
Residuals:
Min 1Q Median 3Q Max
-11.125 -5.918 -0.675 2.975 26.485
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 23.4536 11.9975 1.955 0.0663 .
eduy 2.1476 0.9855 2.179 0.0428 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.032 on 18 degrees of freedom
Multiple R-squared: 0.2087, Adjusted R-squared: 0.1648
F-statistic: 4.749 on 1 and 18 DF, p-value: 0.04285単回帰分析の結果，教育年数の回帰係数は，2.148となり，p値が0.043であり統計的に有意な正の関係があることがわかった。 つまり，教育年数が1年上昇すると職業威信スコアが2.14上がる。
次に，独立変数に年齢を加えた重回帰分析を行う。 \text{職業威信スコア} = \alpha + \beta_1 \text{教育年数} + \beta_2 \text{年齢} + \varepsilon
Call:
lm(formula = job_sc ~ eduy + age, data = chap11)
Residuals:
Min 1Q Median 3Q Max
-12.705 -7.210 -0.310 4.498 23.427
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.7739 14.8724 0.926 0.3673
eduy 2.3976 1.0068 2.381 0.0292 *
age 0.1409 0.1292 1.091 0.2906
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8.985 on 17 degrees of freedom
Multiple R-squared: 0.2605, Adjusted R-squared: 0.1735
F-statistic: 2.994 on 2 and 17 DF, p-value: 0.0769重回帰分析の結果，年齢(age)の回帰係数は0.141，p値は0.291となり，統計的に有意ではなく，回帰係数が0であるという帰無仮説を棄却できなかった。そのため，年齢が職業威信スコアに影響を与えているかどうかは分からない。 次に，教育年数の回帰係数は，2.398，p値は0.029となり，統計的に有意である。したがって，教育年数が1年上昇すると，職業威信スコアが2.398上がることが分かった。
さらに，父親の職業威信スコア(f_job_sc)を独立変数として加えた重回帰分析を行う。
\text{職業威信スコア} = \alpha + \beta_1 \text{教育年数} + \beta_2 \text{年齢} + \beta_3 \text{父親職業威信スコア} + \varepsilon
3変数以上の独立変数をもつ重回帰分析を行う場合は，まず変数間の相関係数を確認することから始める。
cor(chap11[2:5]) age eduy job_sc f_job_sc
age 1.0000000 -0.2276289 0.1175236 0.1036075
eduy -0.2276289 1.0000000 0.4568913 0.4445805
job_sc 0.1175236 0.4568913 1.0000000 0.7271827
f_job_sc 0.1036075 0.4445805 0.7271827 1.0000000すると，職業威信スコア(job_sc)と父親の職業威信スコア(f_job_sc)の相関係数が0.727と相当高いため，両変数を独立変数に組み込んだ重回帰分析では，多重共線性(multi-colinearity)の影響を受ける可能性があるため，注意して分析を進める。 次に偏相関係数を確認する。
pacman::p_load(ppcor)
pcor.test(chap11$job_sc, chap11$eduy, chap11$f_job_sc)| estimate | p.value | statistic | n | gp | Method |
|---|---|---|---|---|---|
| 0.2172802 | 0.3715641 | 0.9177958 | 20 | 1 | pearson |
このように，父親の職業威信スコアをコントロールした場合の職業威信スコアと教育年数の偏相関係数が0.217となり，相関係数0.457から大きく減少している。 これは教育年数と職業威信スコアの関係に，父親の職業威信スコアが影響を与えていることを表している。
これを踏まえて，重回帰分析を行う。
Call:
lm(formula = job_sc ~ eduy + age + f_job_sc, data = chap11)
Residuals:
Min 1Q Median 3Q Max
-10.4969 -4.9509 -0.7485 4.5334 11.3160
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -28.05699 17.34783 -1.617 0.12535
eduy 0.93974 0.91482 1.027 0.31959
age 0.05908 0.10573 0.559 0.58400
f_job_sc 1.29877 0.39395 3.297 0.00455 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.147 on 16 degrees of freedom
Multiple R-squared: 0.5596, Adjusted R-squared: 0.4771
F-statistic: 6.778 on 3 and 16 DF, p-value: 0.0036813つのモデルの結果を並べた表を作表する。 ここでは，stargazer()を用いる。
| job_sc | |||
| (1) | (2) | (3) | |
| eduy | 2.15** | 2.40** | 0.94 |
| (0.99) | (1.01) | (0.91) | |
| age | 0.14 | 0.06 | |
| (0.13) | (0.11) | ||
| f_job_sc | 1.30*** | ||
| (0.39) | |||
| Constant | 23.45* | 13.77 | -28.06 |
| (12.00) | (14.87) | (17.35) | |
| N | 20 | 20 | 20 |
| Adjusted R2 | 0.16 | 0.17 | 0.48 |
| F Statistic | 4.75** | 2.99* | 6.78*** |
先ほどの結果と大きく異なり，父親の職業威信スコアの回帰係数が1.299， p値は0.005と，職業威信スコアと統計的に有意に正の関係にあることが分かる。 また，教育年数(eduy)が統計的に有意でなくなっている。 このことから，父親の職業威信スコアが，子供の教育年数に正の影響を与えており，その結果，子供の職業威信スコアが高くなっている，という因果関係が予想される。