9日目 : ミニレポート

データの説明

Wooldridge “Introductory Econometrics: A Modern Approach”のデータセットを利用して、分析の練習をします。 RでWooldridgeテキストのデータセットが利用できるようになるパッケージwooldridgeを用います。今回は，このwooldridgeパッケージに収録されているwage2を用いるので、以下のように必要なパッケージをpacmanパッケージのp_load()関数で読み出して、data()関数でwage2を読み込みます。

pacman::p_load(
  tidyverse,  # データ操作
  wooldridge, # wooldridgeのデータ
  stargazer, # 回帰分析の表
  rockchalk, # 回帰分析の表
  corrr,
  corrplot)
data("wage2")

データセットのうち，以下の変数を用いる。

wage : 月収（ドル）今回の従属変数
hours : 平均週労働時間
IQ : IQスコア
educ : 教育年数
exper : 経験年数
tenure : 勤続変数
age : 年齢
married : 結婚ダミー
black : 黒人ダミー
south : 南部在住ダミー
sibs : きょうだいの人数
brthord : 出生順
meduc : 母の教育
feduc : 父の教育

このデータセットwage2を用いて，賃金(wage)(月収でドル)を従属変数とした次の分析を行います。

主たる独立変数を1つ選ぶ（連続変数から選ぶ）
別の独立変数を4つ以上選ぶ（連続変数とダミー変数を少なくとも1つずつ選ぶ）
従属変数と独立変数(合計5個以上)の相関行列を作成する。ただし，係数のみ記載すれば良い（有意水準のアスタリスクはいらない）。
以下の回帰分析を行い，表にまとめる。

モデル1：賃金と主たる独立変数の単回帰分析
モデル2：賃金と独立変数(5個以上)の重回帰分析
モデル3：独立変数とダミー変数の交互作用項を加えた重回帰分析を行う。中心化は行わなくてもよい。

交互作用項を図示する
結果を文章で説明する。

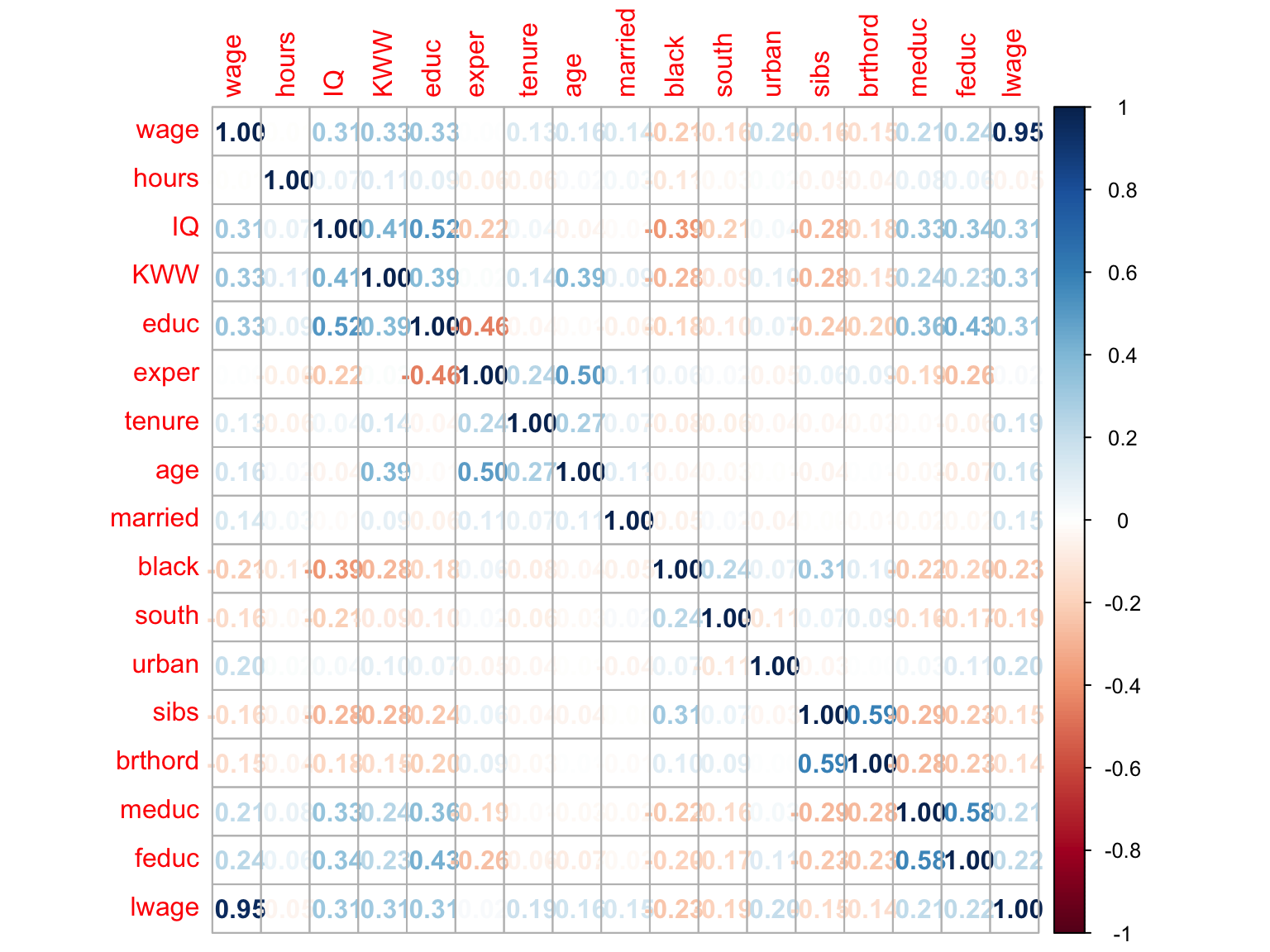
相関行列

いきなり回帰分析をするのではなく、まずは変数間の関係を確認するために、wage2に収録されている変数間の相関係数行列を作成します。基本関数cor()とcorrplotパッケージのcorrplot()関数を用いて相関行列の表を作成します。

wage2 |>
  cor(use = "pairwise.complete.obs") |>
  corrplot::corrplot(method = "number")

この表より，賃金wageと強い線形関係がある変数には，IQ，knowledge of world of work score KWW、教育年数educ，父親の教育年数feduc，母親の教育年数meducがあることが分かりました。

単回帰分析

1つの変数で1つの変数を説明する単回帰分析をやってみます。ここでは、賃金wageを従属変数，教育年数educを独立変数とした次の回帰モデルを推定します。

wage_i = \beta_0 + \beta_1 educ_i + \varepsilon_i

回帰モデルを推定するためには、lm()関数を用います。 lm()関数は引数として、 - formula：回帰モデルの数式 - data：データフレーム

を指定します。

# 回帰モデルの推定
reg01 <- lm(wage ~ educ, data = wage2)
summary(reg01)


Call:
lm(formula = wage ~ educ, data = wage2)

Residuals:
    Min      1Q  Median      3Q     Max 
-877.38 -268.63  -38.38  207.05 2148.26 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  146.952     77.715   1.891   0.0589 .  
educ          60.214      5.695  10.573   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 382.3 on 933 degrees of freedom
Multiple R-squared:  0.107, Adjusted R-squared:  0.106 
F-statistic: 111.8 on 1 and 933 DF,  p-value: < 2.2e-16

賃金を教育年数で回帰した結果、教育年数educの回帰係数は 60.214 となっており、教育年数が1年増えるごとに、賃金が60.214ドル増加することが分かりました。

重回帰分析

次に，賃金wageを従属変数，教育年数educ，経験年数exper，IQIQ，黒人ダミーblackを独立変数とした重回帰分析を行います。交互作用項として使用する教育年数，経験年数，IQは，各変数から平均値を引いた中心化を行います。これにより、交互作用項の解釈が容易になります。

wage2 <- wage2 |> 
  mutate(
    d_edu = if_else(educ > 16, 1, 0),
    m_educ = educ - mean(educ),
    m_exper = exper - mean(exper),
    m_IQ = IQ - mean(IQ),
  )

\begin{aligned} wage_i &= \beta_0 + \beta_1 educ_i + \beta_2 exper_i + \beta_3 IQ_i + \beta_4 black_i + \varepsilon_i\\ wage_i &= \beta_0 + \beta_1 educ_i + \beta_2 exper_i + \beta_3 IQ_i + \beta_4 black_i + \beta_5 IQ_i \times black_i + \varepsilon_i \end{aligned}

reg02 <- lm(wage ~ m_educ + m_exper + m_IQ + black + d_edu, data = wage2)
summary(reg02)


Call:
lm(formula = wage ~ m_educ + m_exper + m_IQ + black + d_edu, 
    data = wage2)

Residuals:
    Min      1Q  Median      3Q     Max 
-913.56 -243.75  -40.85  191.04 2117.19 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  976.567     14.179  68.874  < 2e-16 ***
m_educ        60.157      8.682   6.929 7.93e-12 ***
m_exper       17.221      3.110   5.537 4.00e-08 ***
m_IQ           3.871      1.004   3.856 0.000123 ***
black       -130.750     39.177  -3.337 0.000879 ***
d_edu        -17.746     51.773  -0.343 0.731859    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 368.9 on 929 degrees of freedom
Multiple R-squared:  0.172, Adjusted R-squared:  0.1675 
F-statistic: 38.59 on 5 and 929 DF,  p-value: < 2.2e-16

上記の重回帰モデルに，経験年数experと結婚marriedの交差項を組み込み，交互作用の検証を行います。交差項を組み込むには、m_educ:m_experのように:を用いて交差項を指定します。

reg03 <- lm(wage ~ m_educ + m_exper + m_IQ + black + m_educ:m_exper, data = wage2)
summary(reg03)


Call:
lm(formula = wage ~ m_educ + m_exper + m_IQ + black + m_educ:m_exper, 
    data = wage2)

Residuals:
    Min      1Q  Median      3Q     Max 
-942.72 -244.63  -36.63  184.96 2106.38 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     989.104     14.434  68.528  < 2e-16 ***
m_educ           62.348      7.204   8.654  < 2e-16 ***
m_exper          19.098      3.205   5.959  3.6e-09 ***
m_IQ              3.778      0.998   3.786 0.000163 ***
black          -128.900     39.059  -3.300 0.001003 ** 
m_educ:m_exper    3.342      1.437   2.326 0.020255 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 367.9 on 929 degrees of freedom
Multiple R-squared:  0.1767,    Adjusted R-squared:  0.1722 
F-statistic: 39.87 on 5 and 929 DF,  p-value: < 2.2e-16

stargazerパッケージを用いて、3つの分析結果をまとめた表を作成します。

stargazer(reg01, reg02, reg03, # 回帰分析の結果
  digits = 2, 
  digits.extra = 0, 
  align = TRUE,
  omit.table.layout = 'n', # IMPORTANT!!!
  keep.stat = c('n', 'adj.rsq', 'f'), 
  df = FALSE,
  type = 'html'
)


	Dependent variable:

	wage
	(1)	(2)	(3)

educ	60.21^***
	(5.69)

m_educ		60.16^***	62.35^***
		(8.68)	(7.20)

m_exper		17.22^***	19.10^***
		(3.11)	(3.20)

m_IQ		3.87^***	3.78^***
		(1.00)	(1.00)

black		-130.75^***	-128.90^***
		(39.18)	(39.06)

d_edu		-17.75
		(51.77)

m_educ:m_exper			3.34^**
			(1.44)

Constant	146.95^*	976.57^***	989.10^***
	(77.71)	(14.18)	(14.43)


Observations	935	935	935
Adjusted R²	0.11	0.17	0.17
F Statistic	111.79^***	38.59^***	39.87^***

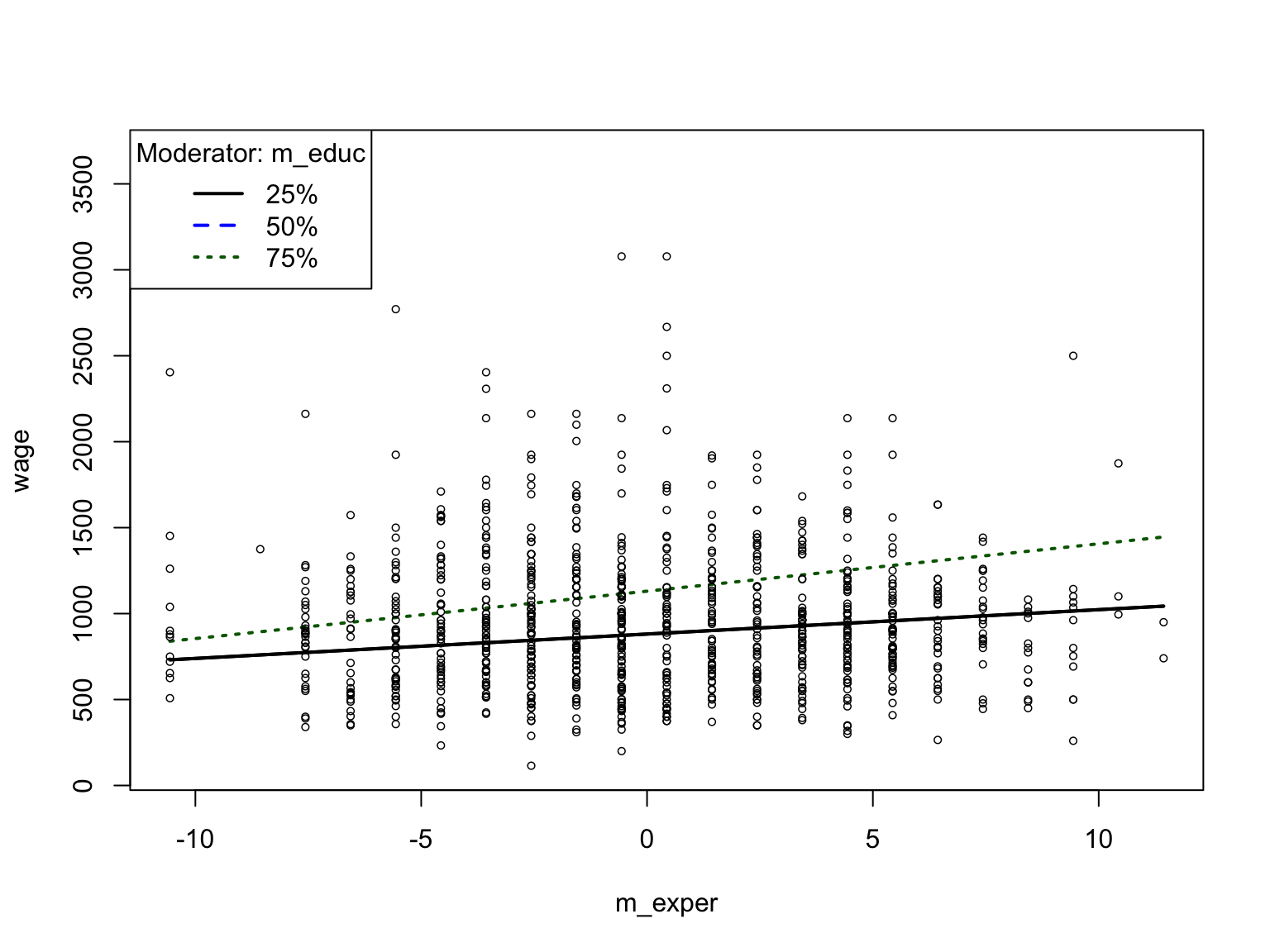
rockchalkパッケージのplotSlopes()関数を使って交互効果を図にすると次のようになります。

plotSlopes(reg03, modx = "m_educ", plotx = "m_exper")