4日目で学習した平均の差の分析を複数回行うことで，3つ以上のグループに平均の差があるかどうか，を検証することができるように思うかもしれませんが、それは誤った検証方法です。 そこでまずは複数回のt検定が誤った結果をもたらす可能性を検討します。
大事なことは，ある事象が生じる確率と複数回思考を行った際に有る事象が少なくとも1回生じる確率は同じでは無い、ということです。 たとえば、サイコロを1つ投げて1の目が出る確率は 1/6 ですが、サイコロを2個同時に振って，少なくとも一方で1の目が出る確率は 1 - (5/6)^2 = 11/36 となり，1つのサイコロで1の目が出る確率 1/6 よりも高くなります。
サイコロを2回振って，少なくとも1個は1の目がでる確率は，2個とも1以外の目が出る確率(5/6)\times (5/6)を1から引けばいい。 つまり，1 - 25/36 = 11/36 となります。
これを一般化すると，次のように表現できます。 ある事象pがn回の試行のうち，1回でも起こる確率は， 1 - (1-p)^n となります。
つまり，t 検定でいう有意確率5％のもとで，2回の試行のうち，1回でも帰無仮説を誤って棄却してしまう確率は，
1 - (1-0.05)^2 = 1 - 0.9025 = 0.0975
となり，有意確率5％の倍近い確率となっていることが分かります。 これが複数回のt検定を行うことが誤った結果をもたらす理由です。
3つ以上のグループ間に，グループ間の差があるかどうかを調べる方法が分散分析(Analysis of Variance: ANOVA)です。 以下では分散分析の考え方を説明します。
データ全体の散らばり(分散)は，グループ間の分散とグループ内の分散に分けることができます。 数式で表現すると，
\sum _{j=1}^k \sum_{i=1}^{n_i}(x_{ij} - \bar x)^2 = \sum _{j=1}^k (\bar x_{.j} - \bar x)^2 + \sum _{j=1}^k \sum _{i=1}^{n_i} (x_{ij} - \bar x_{.j})^2
まず，各種パッケージを呼び出して，データを読み込む。
pacman::p_load(tidyverse, gplots)
d7 <- read_csv("data/chap7.csv")Rows: 30 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): state
dbl (2): ID, kaji
ℹ Use `spec()` to retrieve the full column specification for this data.
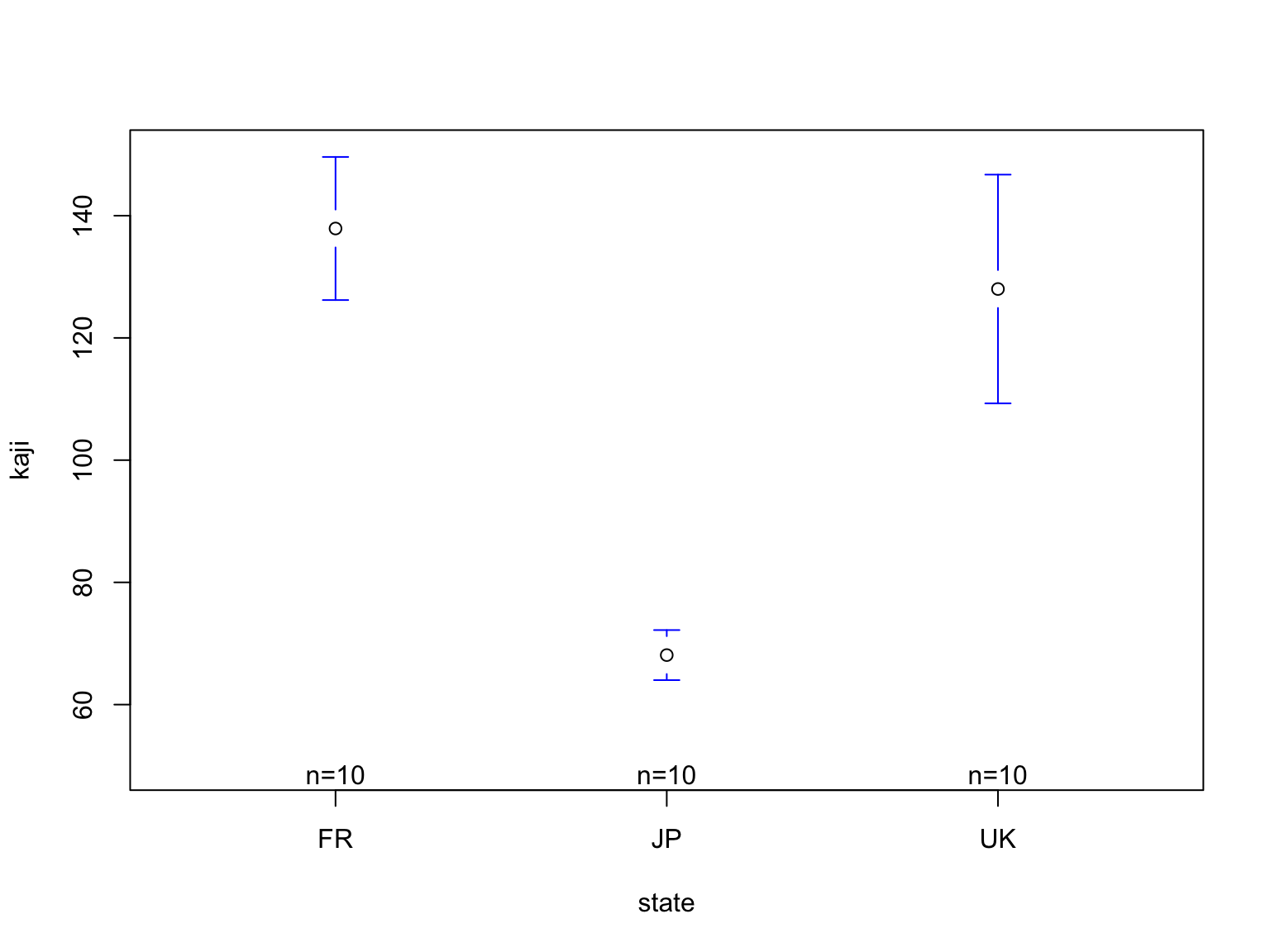
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.国別の男性家事時間を表す仮想データを用いて，国ごとに男性の家事を行う時間に差があるかどうかを示す。 第5章で用いた作図関数plotmeans()を用いて，グラフを書く。
plotmeans(kaji ~ state, data=d7, connect = F, ylim=c(50,150))
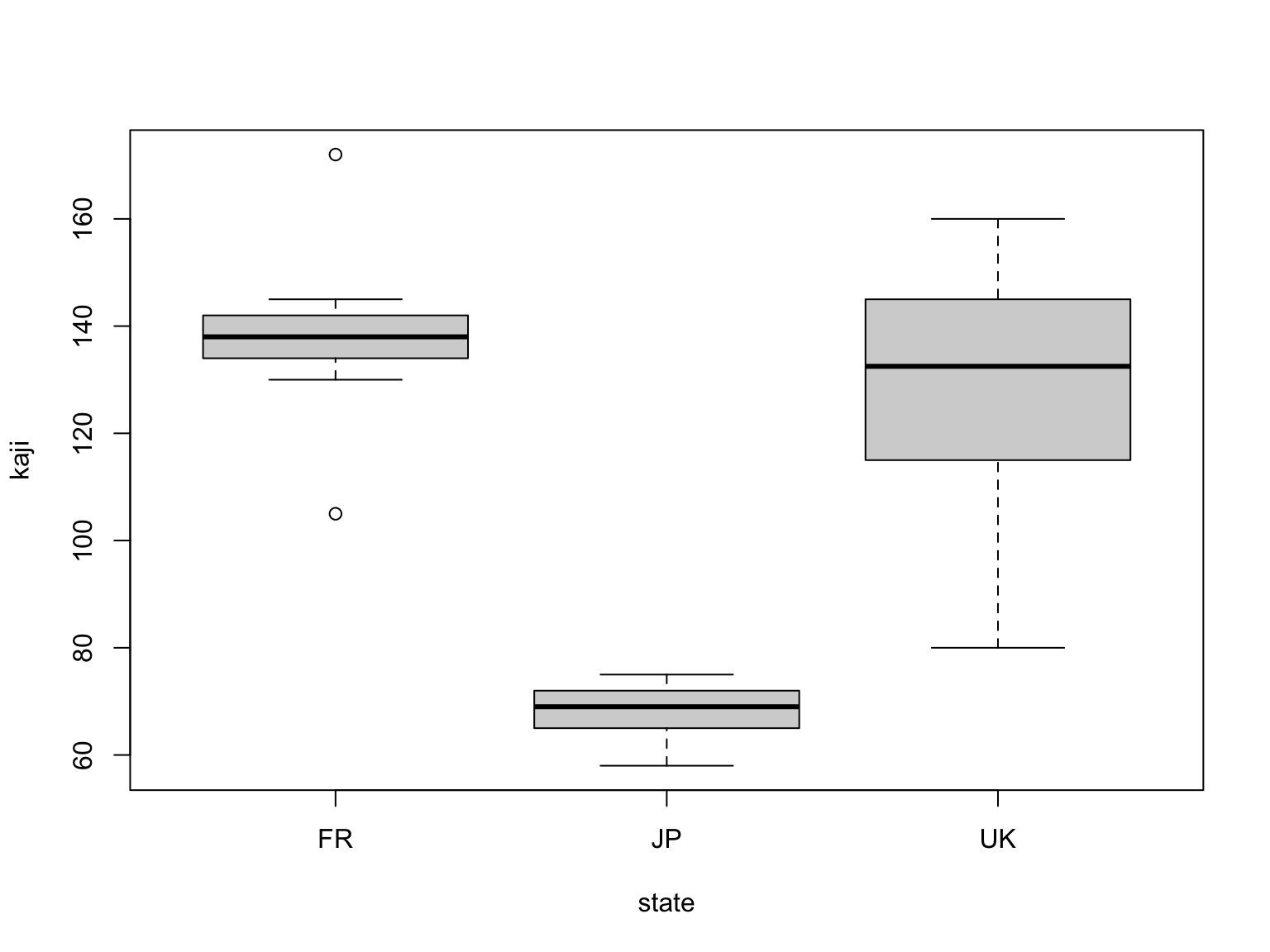
テキストの図7.1のような箱ひげ図も書いてみる。
boxplot(kaji ~ state, data=d7)
次に，oneway.test()を用いて一元配置分散分析を行う。
oneway.test(kaji ~ state, data=d7)
One-way analysis of means (not assuming equal variances)
data: kaji and state
F = 95.559, num df = 2.00, denom df = 13.77, p-value = 8.445e-09多重比較を行うため，Tukey-Kramerの方法をTukeyHSD()を用いる。