15 ロジスティック回帰分析

15.1 ロジスティック関数

「当たったか、外れたか」、「ある会計基準を選択したか、否か」、「ある商品を購入したか、否か」など、結果が二値で表されるような変数を二値変数(binary variable)といい、二値変数を応答変数として回帰分析したいとき、ロジスティック回帰分析が便利です。

事象Aと事象Bのどちらかが起こるとき、事象Aが起こる確率をpとすると、事象Bが起こる確率は1-pとなります。 pは確率を表しているので，0から1の間の値をとります。この事象Aが起こる確率と事象Aが起こらない確率の比をオッズ(odds)といいます。

\frac{p}{1-p}

このオッズは，0から\inftyの間の値をとります。たとえば事象Aが起こる確率が10％と見積もられる場合，オッズは0.1/0.9 = 0.111となります。さらにこのオッズを対数変換して，pの関数f(p)としたものをロジット関数と言います。こうすることで，pは0から1の値をとるとき，f(p)は-\inftyから\inftyの値をとるようになります。

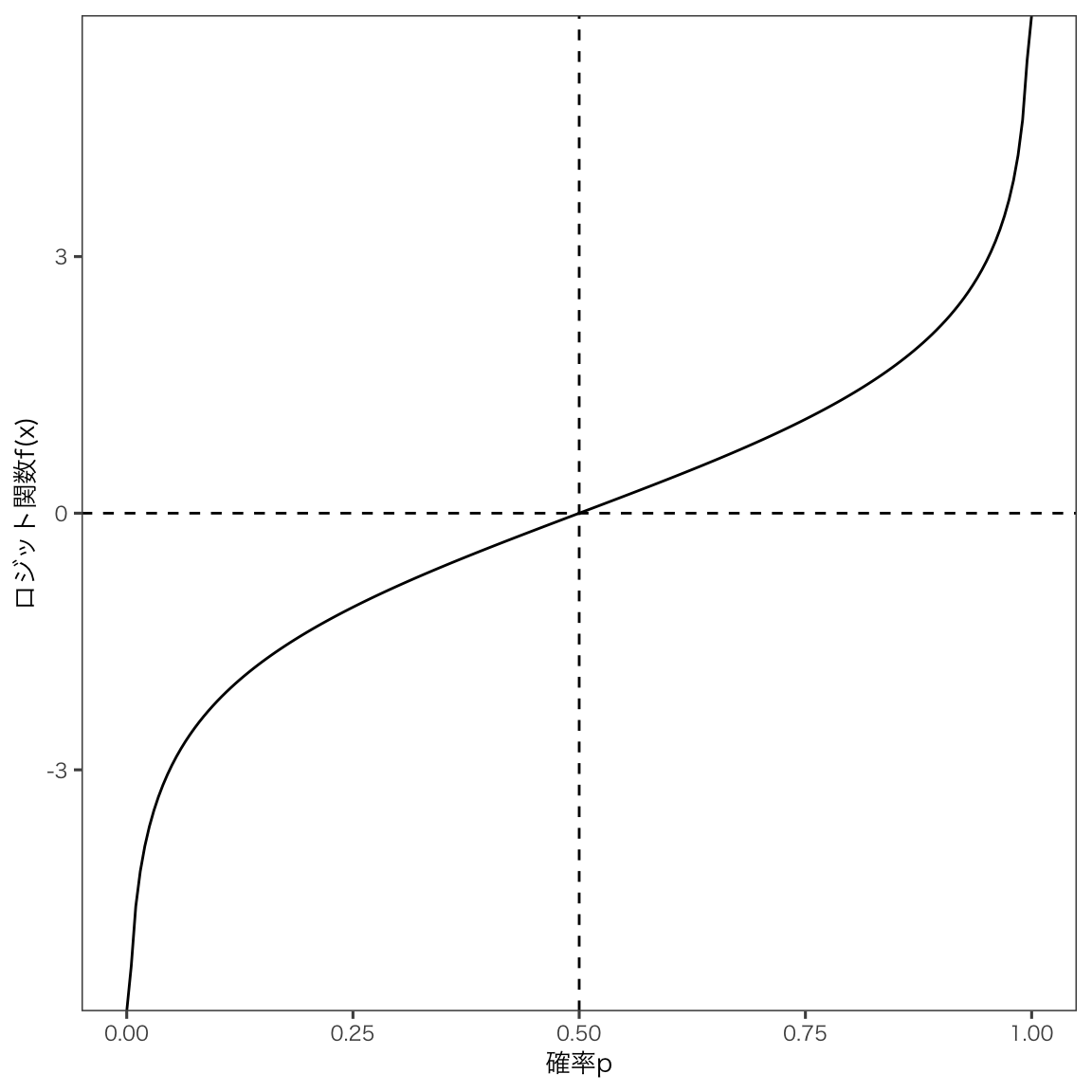
f(p) = \log \left( \frac{p}{1-p} \right) = \log p - \log (1-p)

図で書くとこうなります。

次に，ロジット関数f(p)の逆関数を考えます。対数関数の逆関数は指数関数になるので，先のロジット関数の両辺の指数をとると，次のようになります。

\exp(f(p)) = \frac{p}{1-p}

この式をpについて解くと，次のようになります。

\begin{aligned} p &= \frac{\exp(f(p))}{1 + \exp(f(p))} \\ &= \frac{\frac{\exp(f(p))}{\exp(f(p))}}{\frac{1 + \exp(f(p))}{\exp(f(p))}} \\ &= \frac{1}{\frac{1}{\exp(f(p))}+1} \\ &= \frac{1}{1 + \exp(-f(p))} \end{aligned}

ロジット関数f(p)の逆関数をf^{-1}(x)とすると，f^{-1}(x)は-\inftyから\inftyの値をとるとき，pは0から1の値をとるようになります。これからの分析に必要な関数の形がでてきました。この関数f^{-1}(x)を標準ロジスティック関数と言います。

f^{-1}(x) = \frac{\exp(x)}{1 + \exp(x)} = \frac{1}{1 + \exp(-x)}

標準ロジスティクス関数は次のような形をしています。

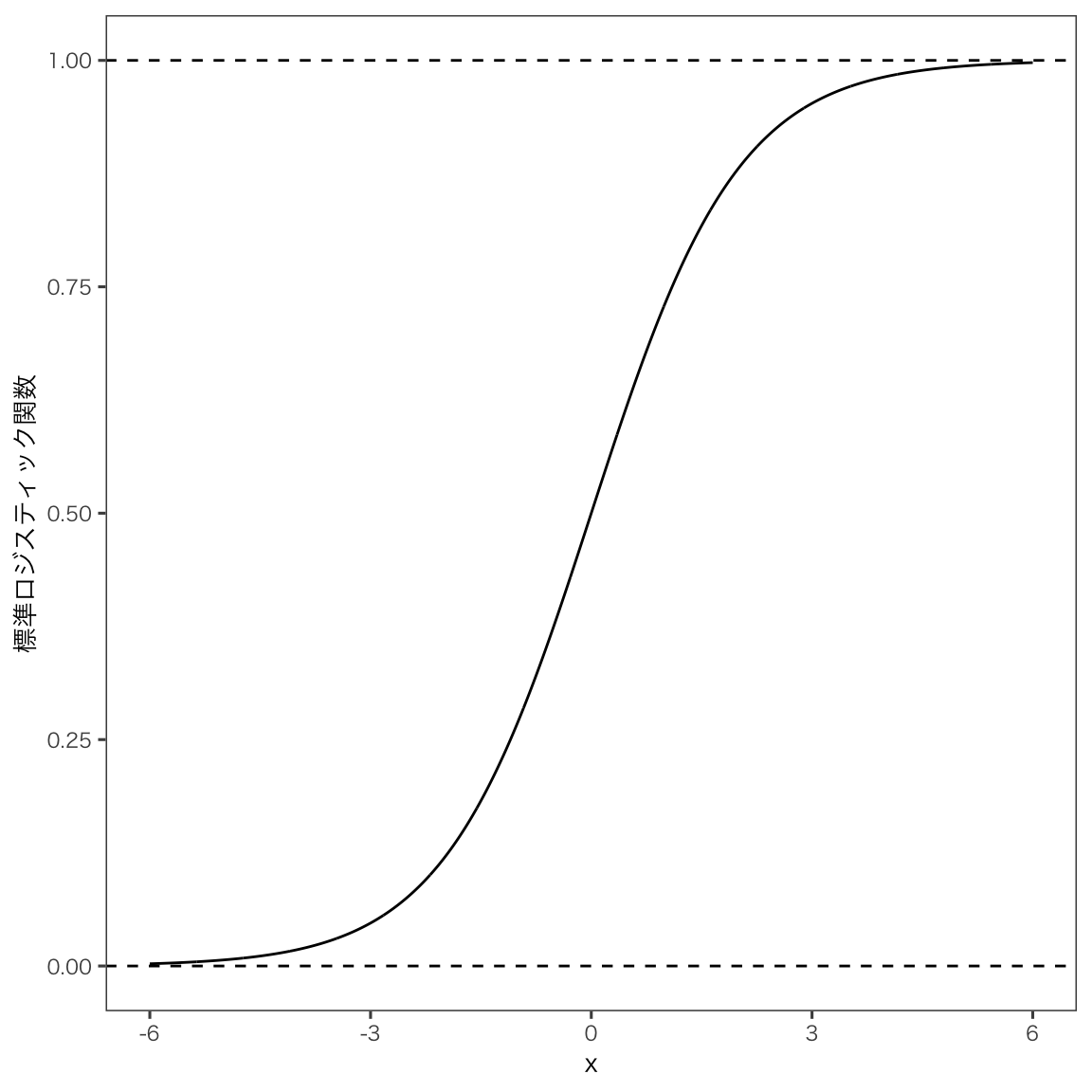
標準ロジスティクス関数の定義域は-\inftyから\inftyですが，xが0のとき，f^{-1}(x)は0.5となります。

応答変数が二値変数となる場合の分析手法で最もよく利用されているものが，ロジスティック回帰分析です。手元の応答変数データは0と1の2種類しかなく、このようなデータを生み出す確率モデルにはベルヌーイ分布が適しています。ベルヌーイ分布は、確率pで1、確率1-pで0をとる確率分布です。この確率pを先ほど導出したロジスティック関数(logistic function)で表します。

\text{logistic}(x) = \frac{\exp(x)}{1 + \exp(x)} = \frac{1}{1 + \exp(-x)}

このロジスティック関数を使って、確率pを次のように表すことができます。

\Pr(y_i = 1) = \text{logistic}(b_0 + b_1x_i) = \frac{1}{1 + \exp(-\beta_0 - \beta_1 x_i)}

この式は、x_iが与えられたときにy_iが1となる確率を表しています。この式を変形すると、次のようになります。

\log \left( \frac{\Pr(y_i = 1)}{1 - \Pr(y_i = 1)} \right) = \beta_0 + \beta_1 x_i

ようやく回帰分析の式になりました。

15.1.1 最尤法

つぎに，この\betaを推定する方法を考えます。この回帰モデルは非線形であるため，モデルと観測値の誤差を最小にする，という最小二乗法を使ってパラメータを推定することはできません。そこで，最尤法(most likelifood method)を使ってパラメータを推定します。最尤法とは，観測値が得られる確率を最大にするようなパラメータを推定する方法で，一定の条件のもとで優れた推定量を与えることが知られています。

最尤法について考える前に，まずロジスティック回帰のモデルの背後にある線形モデルについて考えてみます。観察される応答変数y_iは0か1という二値変数となりますが，その背後には，線形関係があると考えることができます。つまりある閾値y^*を設定して，y_iがy^*より大きいときは1，y^*より小さいときは0となると考えることができます。

y_i = \begin{cases} 1 & \text{if } \beta_0 + \beta_1 x_i + \epsilon_i > y^* \\ 0 & \text{if } \beta_0 + \beta_1 x_i + \epsilon_i \leq y^* \end{cases}

15.2 ロジスティック回帰式の推定

実際にRでロジスティック回帰分析を行う場合は，線形回帰モデルの推定で利用したlm()関数ではなく、glm()関数を使うだけで，ほぼ同じように分析できます。ここでは、不正を行う企業の特徴を分析してみます。

df <- read_csv("data/fraud.csv") %>%
  select(SCODE, Year,NKILM, FEM_NUM, BOARDSIZE, IDOUT_NUM,AGE_AVERAGE, ROA, DASS, FRAUD)
df$Year <- as.factor(df$Year)
df$NKILM <- as.factor(df$NKILM)
glimpse(df)

Rows: 520
Columns: 10
$ SCODE       <dbl> 1515, 1515, 1925, 1925, 8267, 5471, 1925, 5471, 5121, 7878…
$ Year        <fct> 2017, 2018, 2018, 2019, 2018, 2018, 2017, 2019, 2017, 2017…
$ NKILM       <fct> 37, 37, 41, 41, 45, 17, 41, 17, 13, 33, 31, 43, 71, 71, 71…
$ FEM_NUM     <dbl> 0, 0, 1, 1, 3, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1…
$ BOARDSIZE   <dbl> 9, 9, 19, 16, 9, 10, 19, 10, 9, 7, 7, 6, 13, 13, 14, 5, 11…
$ IDOUT_NUM   <dbl> 2, 2, 3, 3, 5, 2, 3, 3, 2, 1, 2, 3, 3, 3, 2, 1, 2, 1, 2, 3…
$ AGE_AVERAGE <dbl> 60, 61, 64, 65, 67, 61, 64, 63, 61, 63, 59, 50, 67, 66, 64…
$ ROA         <dbl> 5.41791, 4.26605, 8.90847, 8.48329, 2.27571, 5.34920, 9.69…
$ DASS        <dbl> 38.4, 37.6, 62.1, 61.7, 81.3, 51.1, 62.5, 50.6, 30.7, 38.8…
$ FRAUD       <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…

ここで、分析に使う変数は次のものです。

SCODEは証券コード
Yearは年度
FEMは女性役員数
BOARDSIZEは取締役会の人数
IDOUT_NUMは独立役員数
AGE_AVERAGEは取締役会の平均年齢
ROAは総資産利益率
DASSは負債比率
FRAUDは不正を行った企業ならば1、そうでなければ0

検証する仮説は「女性取締役が多い企業ほど、会計不正が発生しない」というものです。この仮説を検証するために、ロジスティック回帰分析を行います。

\begin{aligned} FRAUD_{it} &= \beta_0 + \beta_1 FEM_{it} + \beta_2 BOARDSIZE_{it} + \beta_3 IDOUT\_NUM_{it}\\ &+ \beta_4 AGE\_AVERAGE_{it} + \beta_5 ROA_{it} + \beta_6 DASS_{it} \\ &+ Year + \varepsilon_{it} \end{aligned}

これを推定するために、glm()関数を使います。 glm()は一般化線形モデルを推定するための関数で、引数として、formula、family、dataを指定します。ここでは、formulaには推定する式を、familyにはbinomial(link = "logit")を指定します。binomialは二項分布を指定するオプションで、リンク関数としてロジスティック関数の逆関数であるロジット関数を指定しています。dataには、分析に使うデータフレームを指定します。

model_1 <- glm(FRAUD ~ FEM_NUM + BOARDSIZE + IDOUT_NUM + AGE_AVERAGE + ROA + DASS + Year + NKILM,  
               family = binomial(link = "logit"), data = df)
summary(model_1)


Call:
glm(formula = FRAUD ~ FEM_NUM + BOARDSIZE + IDOUT_NUM + AGE_AVERAGE + 
    ROA + DASS + Year + NKILM, family = binomial(link = "logit"), 
    data = df)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.7183  -1.1359   0.0007   1.1303   1.6914  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -2.496247   1.586334  -1.574    0.116    
FEM_NUM     -0.046628   0.130557  -0.357    0.721    
BOARDSIZE    0.014809   0.041592   0.356    0.722    
IDOUT_NUM   -0.155239   0.101865  -1.524    0.128    
AGE_AVERAGE  0.027700   0.020021   1.384    0.166    
ROA          0.006146   0.011142   0.552    0.581    
DASS         0.023332   0.005303   4.400 1.08e-05 ***
Year2018     0.067475   0.227173   0.297    0.766    
Year2019     0.016423   0.251814   0.065    0.948    
Year2020     0.155939   0.335188   0.465    0.642    
NKILM7       0.160140   1.122763   0.143    0.887    
NKILM13     -0.178434   1.779676  -0.100    0.920    
NKILM15      0.375091   1.789514   0.210    0.834    
NKILM17     -0.047652   1.343342  -0.035    0.972    
NKILM19     -0.204360   1.095608  -0.187    0.852    
NKILM21     -0.229660   1.133057  -0.203    0.839    
NKILM23     -0.094920   1.081662  -0.088    0.930    
NKILM27     -0.318377   1.263798  -0.252    0.801    
NKILM31      0.301304   1.175883   0.256    0.798    
NKILM33     -0.087653   1.127659  -0.078    0.938    
NKILM37      0.245728   1.452376   0.169    0.866    
NKILM41     -0.259923   1.079542  -0.241    0.810    
NKILM43     -0.260263   1.071541  -0.243    0.808    
NKILM45     -0.256484   1.130123  -0.227    0.820    
NKILM52     -0.039318   1.251053  -0.031    0.975    
NKILM53     -0.320419   1.205465  -0.266    0.790    
NKILM55     -0.709615   1.790063  -0.396    0.692    
NKILM57     -0.254702   1.331814  -0.191    0.848    
NKILM59     -0.528939   1.761947  -0.300    0.764    
NKILM65     -0.018766   1.373955  -0.014    0.989    
NKILM71      0.045949   1.070176   0.043    0.966    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 720.87  on 519  degrees of freedom
Residual deviance: 696.01  on 489  degrees of freedom
AIC: 758.01

Number of Fisher Scoring iterations: 4