Rows: 4,442
Columns: 17
$ 日経会社コード <chr> "0000001", "0000001", "0000003", "0000003", "0000003", …
$ 企業名称 <chr> "極洋", "極洋", "日本水産", "日本水産", "日本水産", "日…
$ 決算期 <chr> "2006/03", "2007/03", "2006/03", "2007/03", "2008/03", …
$ 決算種別 <dbl> 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10,…
$ 連結基準 <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ 決算月数 <dbl> 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12,…
$ 業種 <dbl> 235341, 235341, 235341, 235341, 235341, 235341, 235341,…
$ 資産合計 <dbl> 65049, 66459, 384819, 404173, 396739, 385462, 383924, 4…
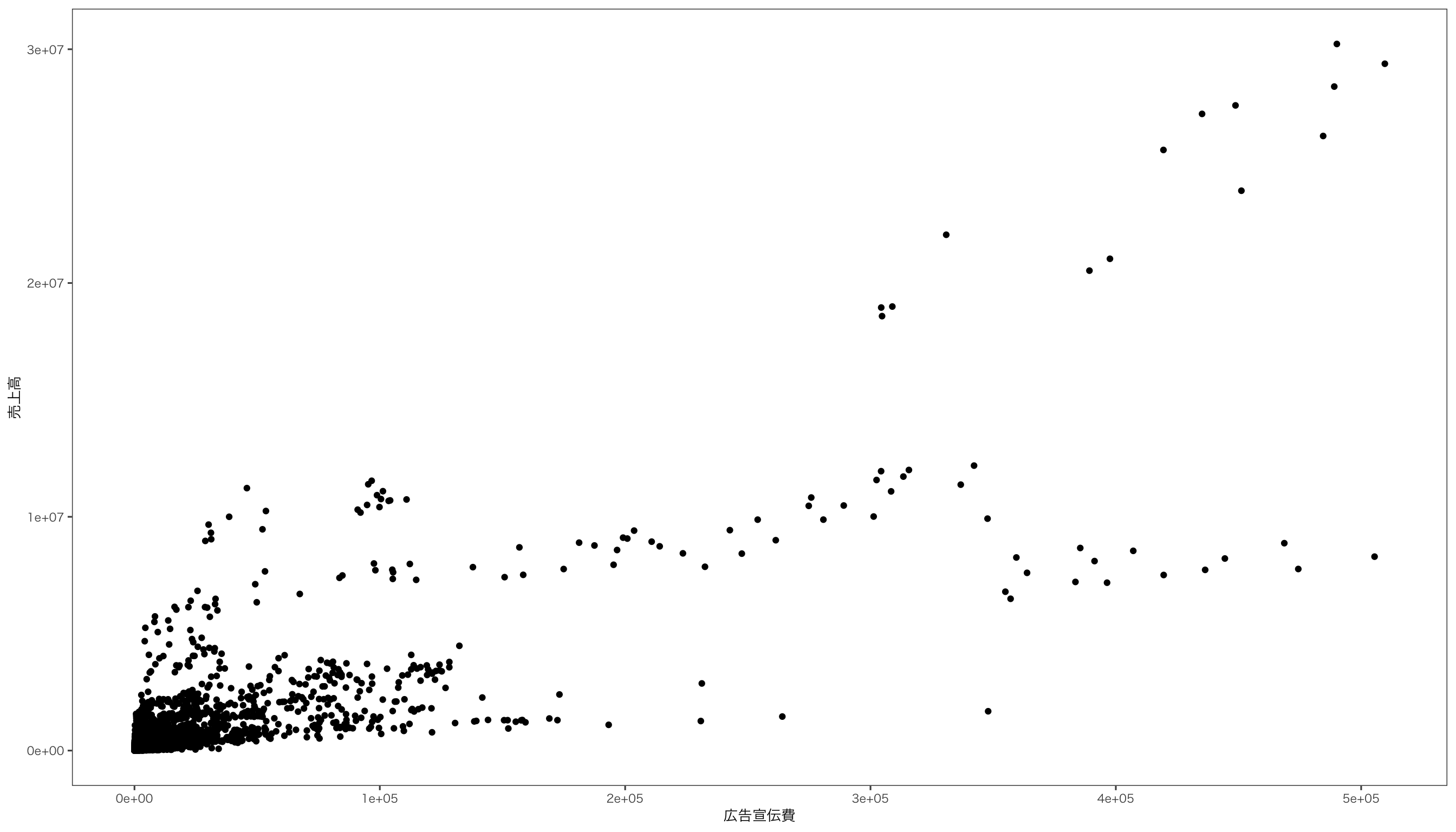
$ 売上高 <dbl> 152899, 157088, 539653, 552871, 533970, 505250, 481574,…
$ 販管費 <dbl> 13702, 14455, 95566, 98200, 100394, 98413, 99938, 10490…
$ 広告宣伝費 <dbl> 304, 279, 2699, 2569, 2953, 2568, 2636, 3160, 3009, 288…
$ 拡販費 <dbl> 111, 158, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
$ 研究開発費 <dbl> 193, 188, 3083, 3377, 3718, 3803, 3994, 4499, 4809, 361…
$ 設備投資額 <dbl> 897, 1841, 17186, 16031, 19105, 28872, 21121, 18633, 16…
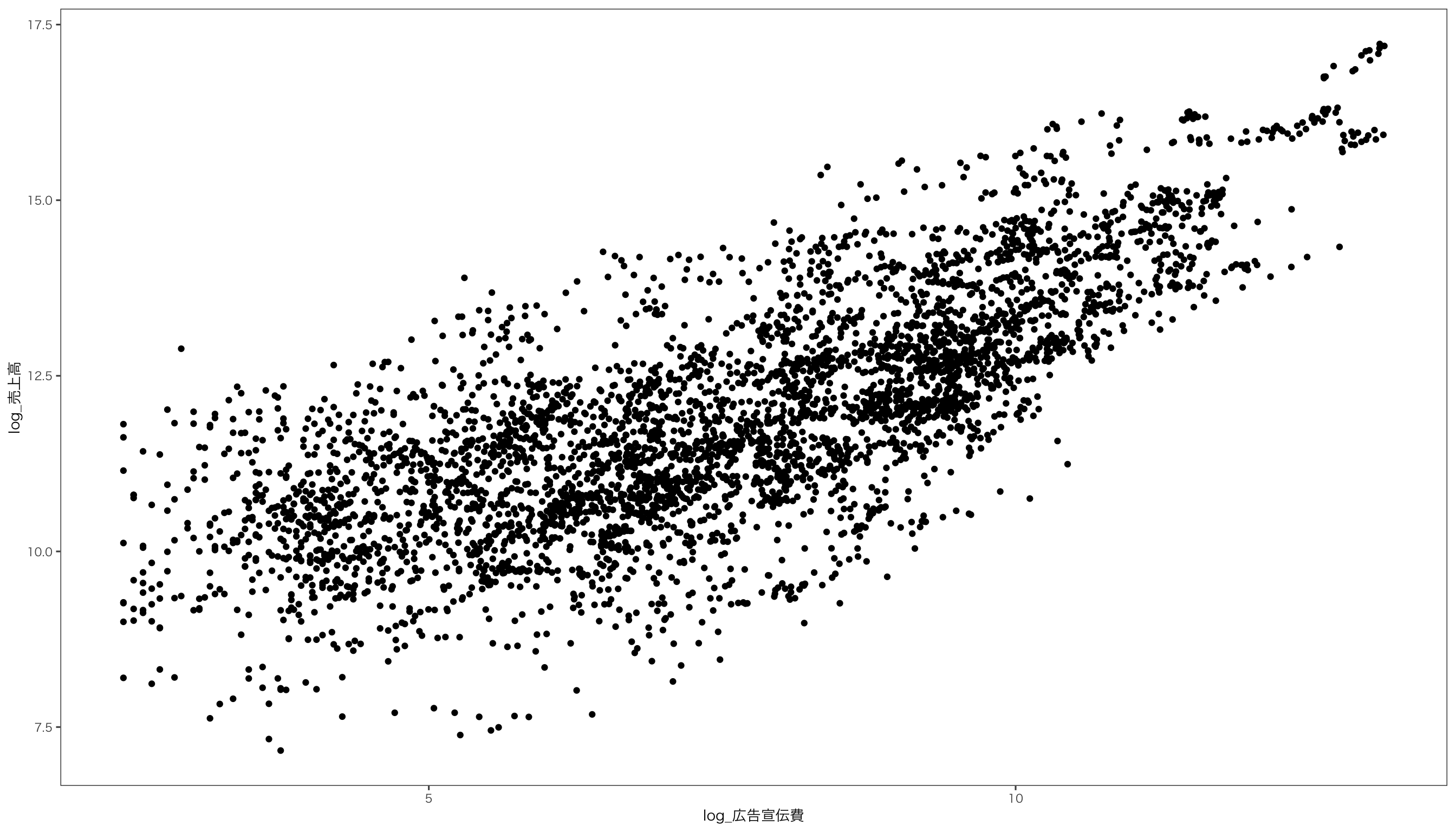
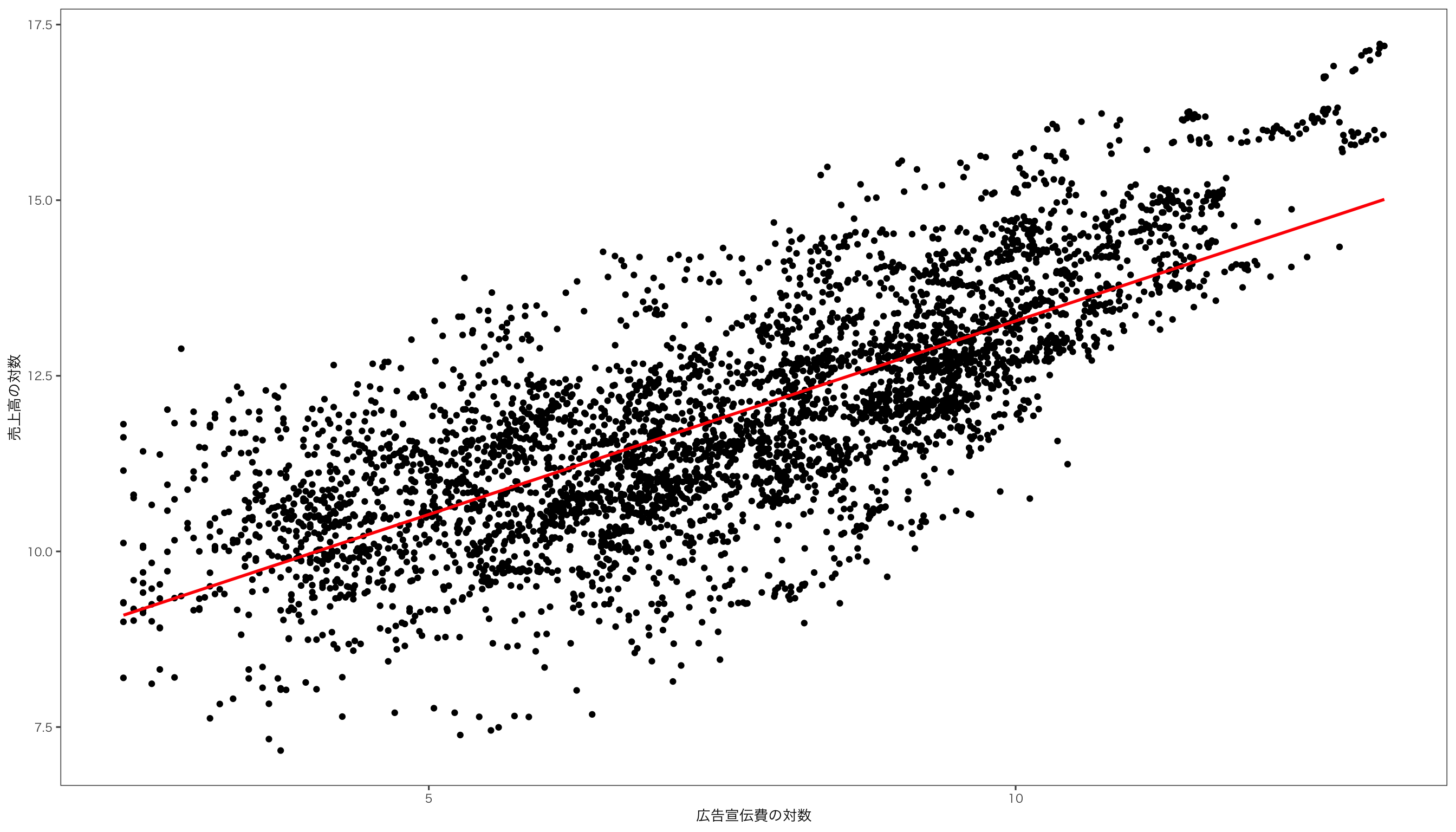
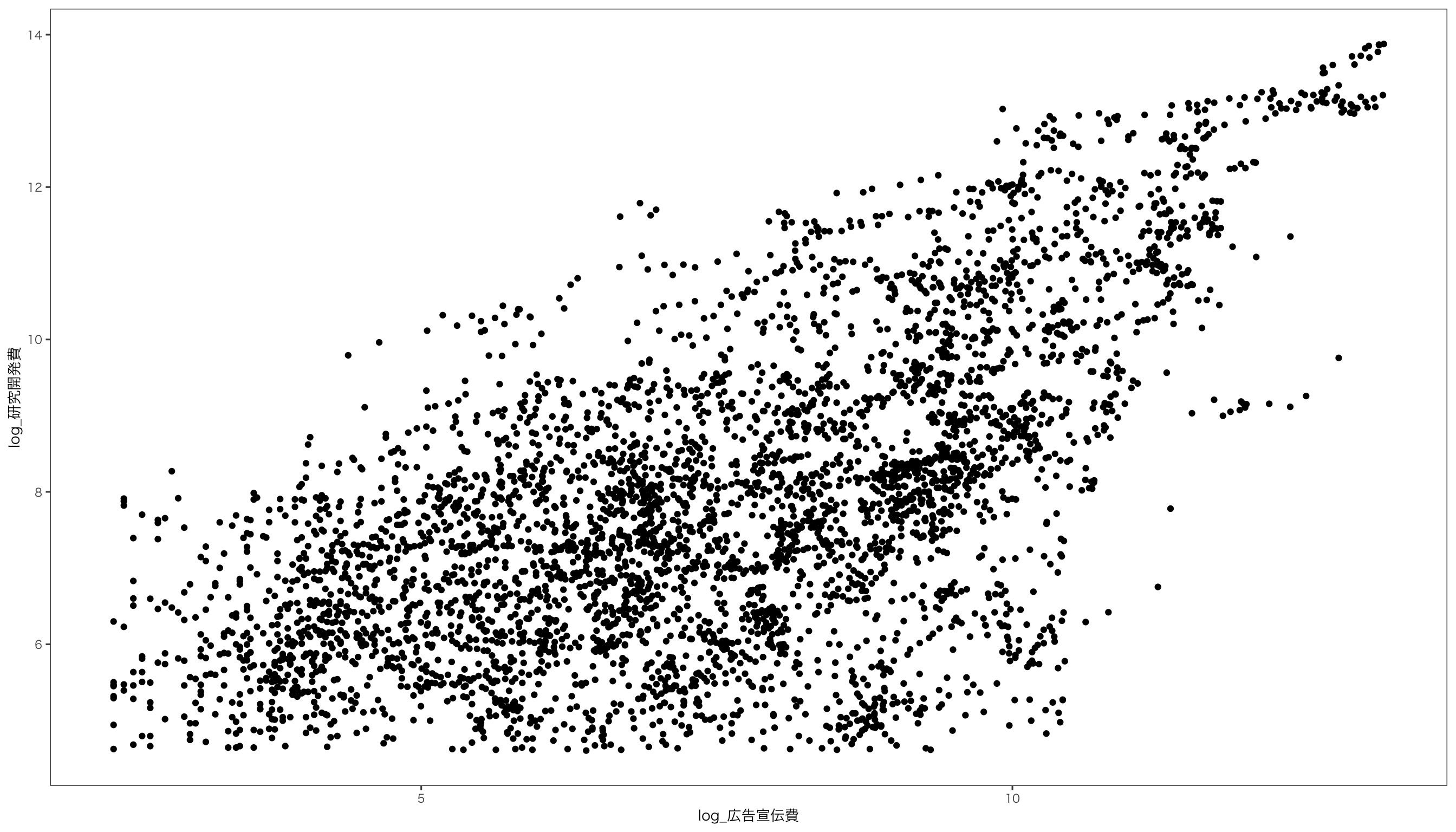
$ log_広告宣伝費 <dbl> 5.717028, 5.631212, 7.900637, 7.851272, 7.990577, 7.850…
$ log_売上高 <dbl> 11.93753, 11.96456, 13.19868, 13.22288, 13.18809, 13.13…
$ log_研究開発費 <dbl> 5.262690, 5.236442, 8.033658, 8.124743, 8.220941, 8.243…