graph LR A[広告宣伝費] --> B[売上高]
11 回帰分析による統計的推定
11.1 単回帰による統計的推定
11.1.1 単回帰モデル
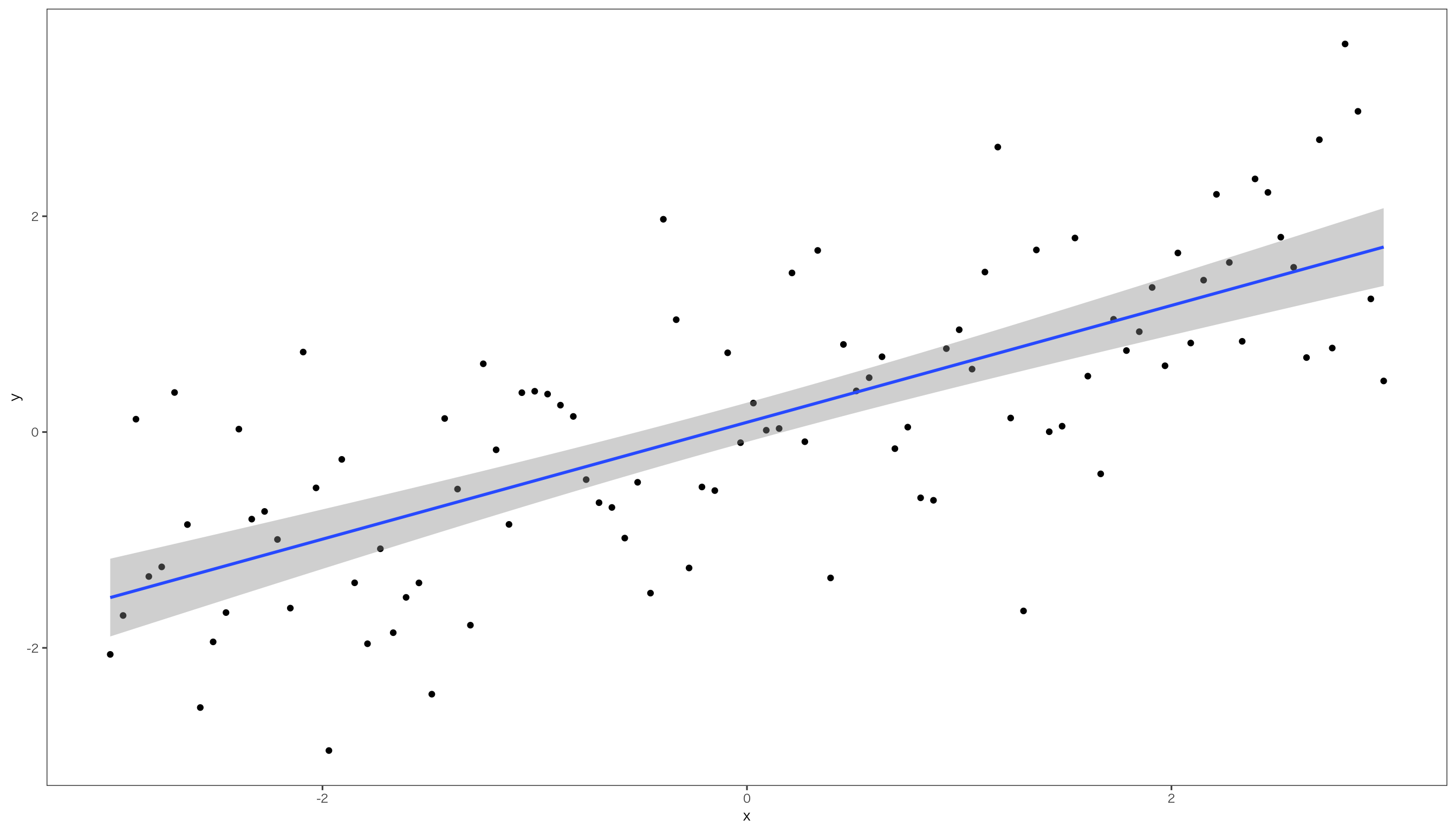
売上高と広告宣伝費の関係を考えるため、前章では散布図(scatter diagram)を使って、2変数の関係を見てみました。 次のような売上高を広告宣伝費で説明するモデルを考えてみます。
この因果関係を明らかにするため、売上高を応答変数Y、広告宣伝費を説明変数Xとして、次のようなモデルを構築します。
Y_i = \beta _0 + \beta_1 X_i
ここで\beta_0と\beta_1は定数です。 したがって、X_iの値が決まれば、応答変数Yの値は一意に決まります。 このようなモデルを決定的モデル(deterministic model)と呼びます。
ただ現実には、広告宣伝費が同じでも売上高が異なることがあります。 そこで売上高の水準が広告宣伝費だけで決まるのではなく、広告宣伝費では説明しきれない要因があることをモデルで表すために、確率変数である誤差項(error term)を回帰モデルに加えたものを考えます。
Y_i = \beta _0 + \beta_1 X_i + \varepsilon_i
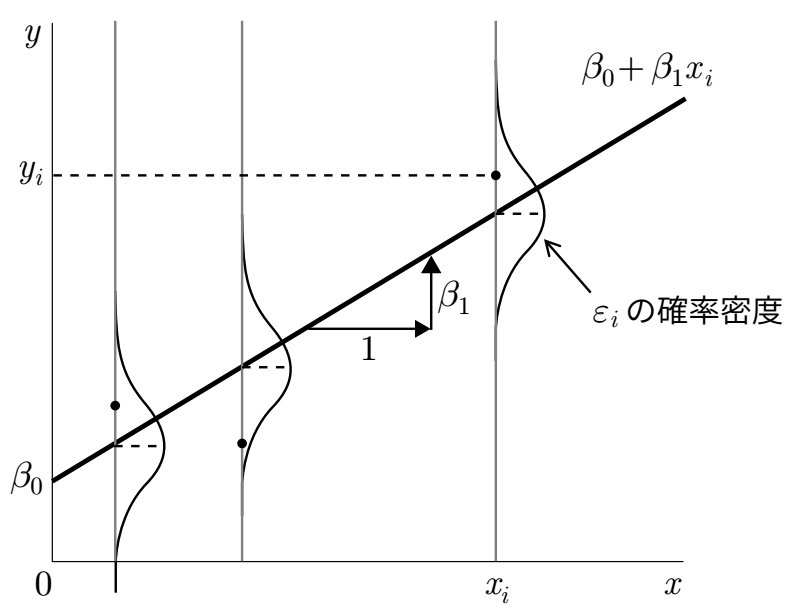
現実のデータで,1つの説明変数が応答変数を完全に説明できる(つまりモデル上にすべてのデータが載っている)ことはほとんどないため、確率変数である誤差項を含めたモデルを確率モデル(probabilistic model)と呼びます。 本書では単回帰モデルとは、\varepsilon_iが正規分布に従うと仮定したモデルを指します。 図で書くと,次のようなモデルです。
この回帰モデルが意味をもつためには、誤差項\varepsilon_iが平均0で分散\sigma^2の正規分布に従うという仮定が必要です。
11.1.2 信頼区間と仮説検定
11.2 重回帰分析による統計的推定
11.2.1 重回帰モデル
重回帰でも単回帰でも統計的推定に変わりはありません。 重回帰モデルを以下のように表します。
Y_i = \beta _0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_p x_{ik} + \varepsilon_i
この回帰係数\betaの推定値bを求めることが統計的推定です。
企業の売上高は、前年度の広告宣伝費と研究開発費で説明できる、つまり前年度の広告宣伝費と研究開発費が高いほど、売上高が高くなるのかどうかを考えてみます。
\text{売上高}_t = \beta_0 + \beta_1 \text{広告宣伝費}_{t-1} + \beta_2 \text{研究開発費}_{t-1} + \varepsilon_t
ではこの回帰モデルを推定するためのデータを読み込むため、tidyverseのreadrパッケージのread_csv()関数を使って、作業ディレクトリのdataフォルダの中に保存されているadv_2023.csvを読み込みます。
df <- read_csv("data/adv_2023.csv")重回帰モデルを推定するには、基本関数のlm()を使います。 重回帰モデルの場合、複数の説明変数があるため+でつなげていきます。
res <- lm(売上高 ~ lag(研究開発費) + lag(広告宣伝費), data = df)
coef(res) (Intercept) lag(研究開発費) lag(広告宣伝費)
1.004955e+05 1.716521e+01 6.913074e+00 上記の推定結果から、
\text{売上高} = 0.00000 + 0.1716 \text{研究開発費}_{t-1} + 6.8131 \text{広告宣伝費}_{t-1} であることが分かりました。
11.2.2 信頼区間と仮説検定
先ほどの回帰係数の推定結果は,1サンプルからの結果であり,サンプルの数を増やせば推定値の分布ができるのは,単回帰分析と同じなので, ここでも同じ方法で信頼区間を求めることが出来ます。 単回帰分析の場合,切片と回帰係数の2つが推定するパラメータなので,自由度がn-2のt分布を利用しました。 説明変数がk個ある重回帰分析の推定で利用するt分布の自由度は,n-k-1になります。 100(1-\alpha)%信頼区間は,
b_m - t _{n-k-1, \frac{\alpha}{2}} SE(b_m) \leq \beta_m \leq b_m + t_{n-k-1, \frac{\alpha}{2}} SE(b_m)
のように計算できます。 先ほど推定した重回帰分析の結果を再度確認してみます。
summary(res)
Call:
lm(formula = 売上高 ~ lag(研究開発費) + lag(広告宣伝費),
data = df)
Residuals:
Min 1Q Median 3Q Max
-12323473 -100139 -69328 20239 19099811
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.005e+05 1.257e+04 7.995 1.58e-15 ***
lag(研究開発費) 1.717e+01 2.639e-01 65.039 < 2e-16 ***
lag(広告宣伝費) 6.913e+00 5.164e-01 13.386 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 862200 on 5171 degrees of freedom
( 23266 個の観測値が欠損のため削除されました )
Multiple R-squared: 0.7853, Adjusted R-squared: 0.7853
F-statistic: 9460 on 2 and 5171 DF, p-value: < 2.2e-16ここから信頼区間を計算するためには,サンプルサイズnと説明変数の数kから自由度df = n - k -1を求め, そのもとで特定の有意水準を設定して,関数qt()を使ってt値を計算します。 先ほどの重回帰の例だと,サンプルサイズは28440,説明変数の数は2なので,有意水準5%の両側検定を行う場合のt値は,
n <- nrow(df) # サンプルサイズ
k <- 2 # 説明変数の数
freedom <- n - 2 - 1
p <- 0.025 # 両側5%なので片側2.5%
qt(p, freedom , lower.tail = F)[1] 1.960047するとt値は,1.96と計算できました。
11.2.2.1 仮説検定
重回帰分析で検証したい仮説は,説明変数が応答変数に影響を与えるか否かですが,複数の説明変数があるため,仮説には2つのパターンがあります。 1つ目は,回帰係数のすべてがゼロである,という帰無仮説です。 構築した回帰モデルの説明変数の中に,応答変数に影響を与えるものが1つもない,という仮説です。 \begin{aligned} H_0 : &\beta _1 = \beta _2 = \cdots = \beta_k = 0\\ H_A : &\beta _1 \not = 0 \text{ or } \beta _2 \not = 0 \text{ or } \cdots \text{ or } \beta _k \not = 0 \end{aligned}
2つ目は,回帰係数の中に少なくとも1つはゼロではない,という仮説です。 この仮説だと,個々の説明変数が応答変数に与える影響を別々に考え,説明変数ごとに回帰係数がゼロとなるかどうかを調べることになります。
\begin{aligned} H_{01}: \beta _1 &= 0, & H_{a1} : \beta _1 \not = 0 \\ H_{02}: \beta _1 &= 0, & H_{a2} : \beta _1 \not = 0 \\ \vdots \\ H_{0k}: \beta _k &= 0, & H_{ak} : \beta _k \not = 0 \\ \end{aligned}
11.2.2.2 1つの仮説の検定
すべての回帰係数がゼロかどうかを検定するためには,F分布という確率分布を用います。 F分布の確率密度関数の導出は難しいのでここでは省略します F分布の下で,自由度n - k -1で説明変数の数がk個であるときの検定統計量F_0は,次のように計算できます。
\begin{aligned} F_0 = \frac{R^2}{1 - R^2} \frac{n - k - 1}{k} = \displaystyle \frac{\sum (\hat y - \bar y)^2}{k} \div \frac{\sum e_i-2}{n - k - 1} \end{aligned}
ここでR^2は決定係数です。 この検定統計量F_0を用いたF検定の結果は,lm()関数で推定した結果のsummary()関数で確認できます。
summary(res)
Call:
lm(formula = 売上高 ~ lag(研究開発費) + lag(広告宣伝費),
data = df)
Residuals:
Min 1Q Median 3Q Max
-12323473 -100139 -69328 20239 19099811
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.005e+05 1.257e+04 7.995 1.58e-15 ***
lag(研究開発費) 1.717e+01 2.639e-01 65.039 < 2e-16 ***
lag(広告宣伝費) 6.913e+00 5.164e-01 13.386 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 862200 on 5171 degrees of freedom
( 23266 個の観測値が欠損のため削除されました )
Multiple R-squared: 0.7853, Adjusted R-squared: 0.7853
F-statistic: 9460 on 2 and 5171 DF, p-value: < 2.2e-16結果の最後の行でF-statistic: 9460 on 2 and 5171 DF, p-value: < 2.2e-16とあり,自由度2と5171のF分布で検定した結果,検定統計量F_0は9460であり,p値はほぼゼロとなりました。 つまり,帰無仮説である「すべての回帰係数がゼロ」は棄却され,少なくとも一つの回帰係数はゼロではない,という対立仮説が採択されました。
t分布と同様にF分布を用いた検定の臨界値は基本関数qf()で計算できます。 先ほどの例だと,サンプルサイズは28440,説明変数の数は2なので,有意水準5%の両側検定を行う場合のt値は,
p = 0.05
f1 <- 2
f2 <- 5171
qf(p,f1,f2,lower.tail =F)[1] 2.997468となり,2.9975という臨界値が得られた。 先ほどの推定結果からF値が9460と,臨界値を遙かに超える値であったため,帰無仮説は棄却された。
11.2.2.3 回帰係数の個別的検定
第2の仮説のパターンである個々の回帰係数の検定について考えてみましょう。 売上高を研究開発費と広告宣伝費で説明しようとした重回帰モデルだと,次の2つの仮説を検定することになります。
\begin{aligned} \text{研究開発費} H_{01} : \beta_1 = 0, & H_{a1} : \beta_1 \not = 0 \\ \text{広告宣伝費} H_{02} : \beta_1 = 0, & H_{a2} : \beta_1 \not = 0 \end{aligned}
回帰係数の個別的検定は,単回帰分析と同様にt検定を用います。 この分析結果も,summary()関数で確認できます。
summary(res)
Call:
lm(formula = 売上高 ~ lag(研究開発費) + lag(広告宣伝費),
data = df)
Residuals:
Min 1Q Median 3Q Max
-12323473 -100139 -69328 20239 19099811
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.005e+05 1.257e+04 7.995 1.58e-15 ***
lag(研究開発費) 1.717e+01 2.639e-01 65.039 < 2e-16 ***
lag(広告宣伝費) 6.913e+00 5.164e-01 13.386 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 862200 on 5171 degrees of freedom
( 23266 個の観測値が欠損のため削除されました )
Multiple R-squared: 0.7853, Adjusted R-squared: 0.7853
F-statistic: 9460 on 2 and 5171 DF, p-value: < 2.2e-16Coefficientsの出力結果に,各説明変数の回帰係数の推定値Estimateと標準誤差Std. Error,t値t value,p値Pr(>|t|)が表示されています。 このp値が設定した有意水準より小さい場合,その回帰係数がゼロであるという帰無仮説が棄却され,説明変数が応答変数に影響を与えている,という対立仮説が採択されるのです。
このように複数の説明変数で応答変数を説明しようとする重回帰分析だと,2種類の仮説検証を行うことになります。 気をつける点として,すべての回帰係数がゼロであるという帰無仮説を検証するF検定で,帰無仮説が棄却されたとしても,個別の回帰係数の検定で,すべての検定で帰無仮説を棄却できない,というケースも起こり得ます。 このような結果が出たときは,説明変数どうしの相関が強いときに生じやすいので注意しよう。
重回帰分析の結果を論文などに掲載する場合には,ほぼ決まったフォーマットがあるため,それに従って結果をまとめることになります。 例えば,次のような表を作成することになります。
library(modelsummary)
msummary(res,
stars = TRUE, # p値の有意性を星で表示する
fmt = '%.2f',
gof_omit = "AIC|BIC|Log.Lik.",
output = 'html'
)| (1) | |
|---|---|
| (Intercept) | 100495.49*** |
| (12569.41) | |
| lag(研究開発費) | 17.17*** |
| (0.26) | |
| lag(広告宣伝費) | 6.91*** |
| (0.52) | |
| Num.Obs. | 5174 |
| R2 | 0.785 |
| R2 Adj. | 0.785 |
| RMSE | 861991.65 |
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 |
11.3 まとめ
- 観測値とモデルとの差を表す確率変数である誤差項を含んだ確率的回帰モデルを考えます。
- 単回帰モデル : Y_i = \beta _0 + \beta_1 X_i + \varepsilon_i
- 重回帰モデル : Y_i = \beta _0 + \beta_1 X_{i1} + \cdots + \beta_k X_{ik} + \varepsilon_i
- 確率的誤差項は,平均ゼロの正規分布にしたがう確率変数であると仮定します。
- 回帰分析の目的は,回帰係数\beta_mの推定値b_mの値を求めることです。
- 推定値b_mは標本ごとに異なる値となるため,推定値は分布します。そこで推定値の信頼区間を求めて推定の不確実性を評価します。
- 重回帰モデルの仮説検定は2種類あって,すべての回帰係数がゼロである,というものと,個々の回帰係数がゼロである,というものがあります。前者にはF検定,後者にはt検定を用いて分析します。