変数間の関連性

第8回講義の到達目標は、

• カテゴリー変数間の関連性を調べる方法を学ぶ。

• 2変数の関係を表す統計量を出力できる。

• 統計量から結果を解釈し，意味のある主張をすることができる。

• 第8回講義の到達度検証のための課題は、以下の通りです。

• カテゴリー変数間の関連性を調べる方法を説明できる。

この章では、2つ以上の変数間の関係を調べる方法を学びます。 1つめは、カテゴリー変数間の関係を調べる方法として、クロス集計表とカイ二乗検定を学びます。 2つめは、量的変数間の関係を調べる方法として、相関係数と散布図を学びます。

カテゴリー変数の関連

クロス集計表

カテゴリー変数は、その値がどのカテゴリーに属するかということを表す変数です。 2つのカテゴリー変数の関連性を調べるためにはクロス集計表を作ることが有益です。 例えば、400名のクラスに、男が245名、女が155名います。 また、クラスの中で、メガネをかけている男が41名、メガネを掛けている女が81名いました。 このクロス集計表は次のようなものになります。

	メガネをかけている	メガネをかけていない	合計
男	41	204	245
女	81	74	155
合計	122	278	400

この表から、メガネをかけている人の割合は、男性の中で \(41\div 245 =\) 0.1673469、女性の中で \(81 \div 155 =\) 0.52であることから、女子学生の方がメガネをかけている割合が高いことが分かりました。

カイ二乗検定

このクロス集計表から読み取れる関係が、統計的に意味があるのかどうかを調べるためには、\(\chi ^2\)(カイ二乗)検定を行います。 \(\chi^2\)検定は次のステップで実行します。

1. 帰無仮説として、カテゴリー変数間に関連性はないと仮定
2. その仮定のもとで、観測されたクロス集計表の度数が、理論的に予測される度数と大きく異なるかどうかを検定
3. 予測される度数と観測された度数の差が大きいほど、帰無仮説が棄却される

\(\chi^2\)検定で用いられる統計量は、\(\chi^2\)統計量と呼ばれ、次の式で計算されます。

\[ \chi^2 = \sum_{i=1}^n \sum_{j=1}^m \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \] ここで、\(O_{ij}\)は観測された度数(観測度数)、\(E_{ij}\)は理論的に予測される度数(期待度数)です。\(n\)と\(m\)はカテゴリー変数のカテゴリー数です。 つまり、2つのカテゴリー変数の関連性を調べる場合、\(\chi^2\)統計量は次のように計算されます。

\[ \begin{aligned} \chi^2 &= \frac{(O_{11} - E_{11})^2}{E_{11}} + \frac{(O_{12} - E_{12})^2}{E_{12}} \\ &+ \frac{(O_{21} - E_{21})^2}{E_{21}} + \frac{(O_{22} - E_{22})^2}{E_{22}} \end{aligned} \]

ここで、期待度数\(E\)をどうやって求めるのか、が問題となります。 期待度数の「期待」の意味は、帰無仮説のもとで期待される度数です。

\[ E_{ij} = \frac{O_{i\cdot} \times O_{\cdot j}}{O_{\cdot \cdot}} \] ここで、\(O_{i\cdot}\)は\(i\)行目の合計(横の合計)、\(O_{\cdot j}\)は\(j\)列目の合計(縦の合計)、\(O_{\cdot \cdot}\)は全体の合計です。

先のメガネの例で計算してみます。 観察度数\(O\)は次のようになります。

	メガネをかけている	メガネをかけていない	合計
男	41	204	245
女	81	74	155
合計	122	278	400

男の行合計\(O_{男\cdot}\)は245、女の行合計\(O_{女\cdot}\)は155、メガネ有りの列合計\(O_{\cdot メガネ有}\)は122、メガネなしの列合計\(O_{\cdot メガネ無}\)は278、全体の合計\(O_{\cdot \cdot}\)は400となります。 ここから、期待度数は次のように計算されます。

\[ \begin{aligned} E_{男, メガネ} &= \frac{245 \times 122}{400} = 74.725 \\ E_{男, メガネ無} &= \frac{245 \times 278}{400} = 170.275 \\ E_{女, メガネ} &= \frac{155 \times 122}{400} = 47.275 \\ E_{女, メガネ無} &= \frac{155 \times 278}{400} = 107.725 \end{aligned} \]

よって期待度数\(E\)は次のようになります。

	メガネをかけている	メガネをかけていない	合計
男	74.725	170.275	245
女	47.275	107.725	155
合計	122	278	400

ここから、定義通りに、\(\chi^2\)統計量を計算します。

\[ \begin{aligned} \chi^2 = \frac{(41 - 74.725)^2}{74.725} + \frac{(204 - 170.275)^2}{170.275} + \frac{(81 - 47.275)^2}{47.275} + \frac{(74 - 107.725)^2}{107.725} = 56.51731 \end{aligned} \]

ここで計算した\(\chi^2\)統計量は、自由度1の\(\chi^2\)分布に従うということが知られています。この自由度は、カテゴリー変数のカテゴリー数から1を引いたものです。 ここでは、2カテゴリー同士のクロス集計表なので、自由度は\((2-1) \times (2-1) = 1\)となります。

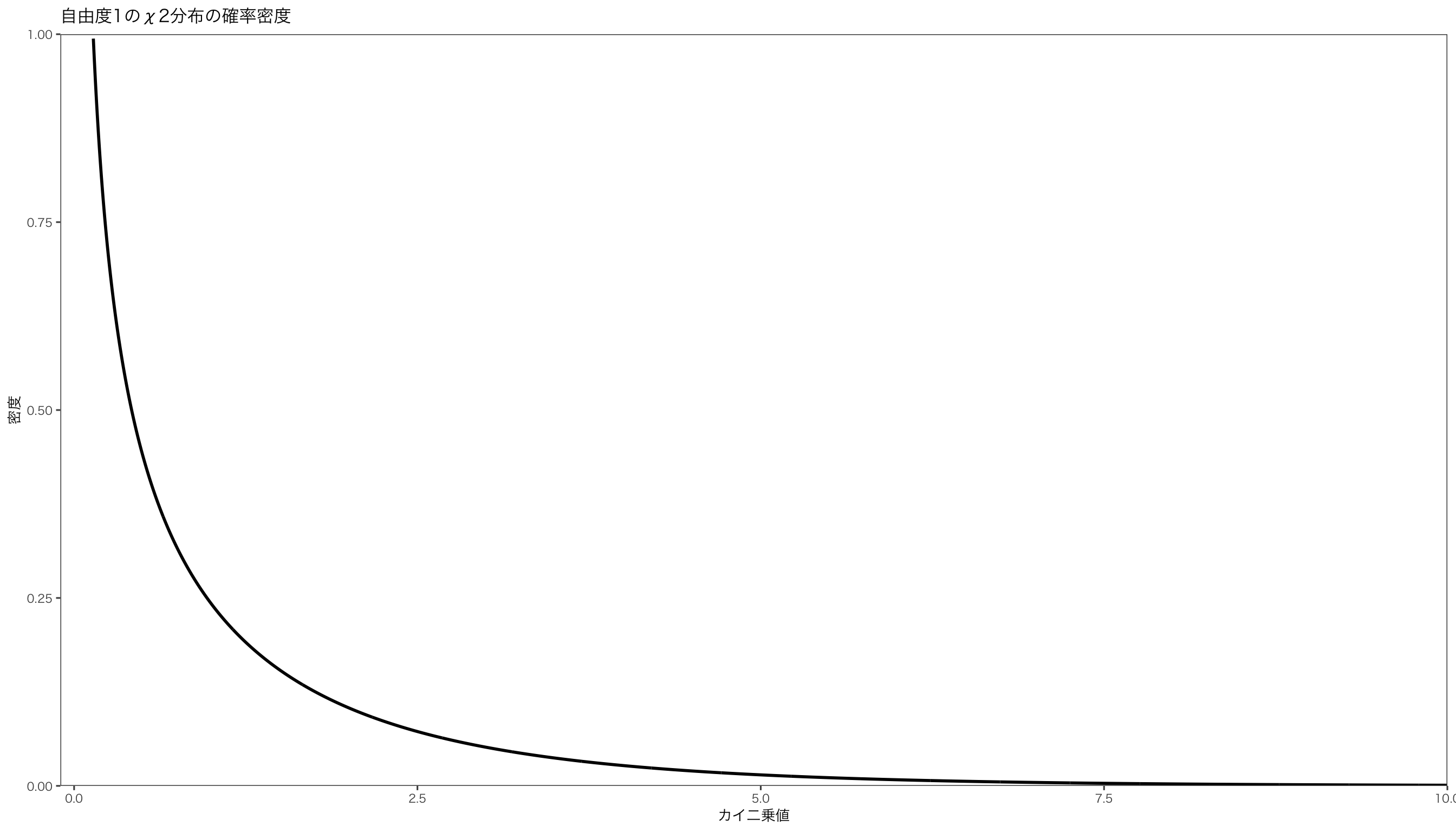
自由度1のカイ二乗分布の確率密度関数は次のようになります。

x = c(1:2500) / 250 # 数列を作成
y1 = dchisq(x,1) # カイ二乗分布の確率密度

df <- data.frame(x, y1) # データフレームを作成
p <- ggplot(df) + aes(x = x,y = y1) # 作図
p <- p + geom_line(size = 1) # 折れ線グラフ
p <- p + ylim(c(0,1)) + ylab("密度") + xlab("カイ二乗値") +
  scale_y_continuous(expand = c(0,0), limits = c(0,1)) +
  scale_x_continuous(expand = c(0,0), limits = c(-0.1,10))
p <- p + ggtitle("自由度1のχ2分布の確率密度") +  mystyle
print(p)

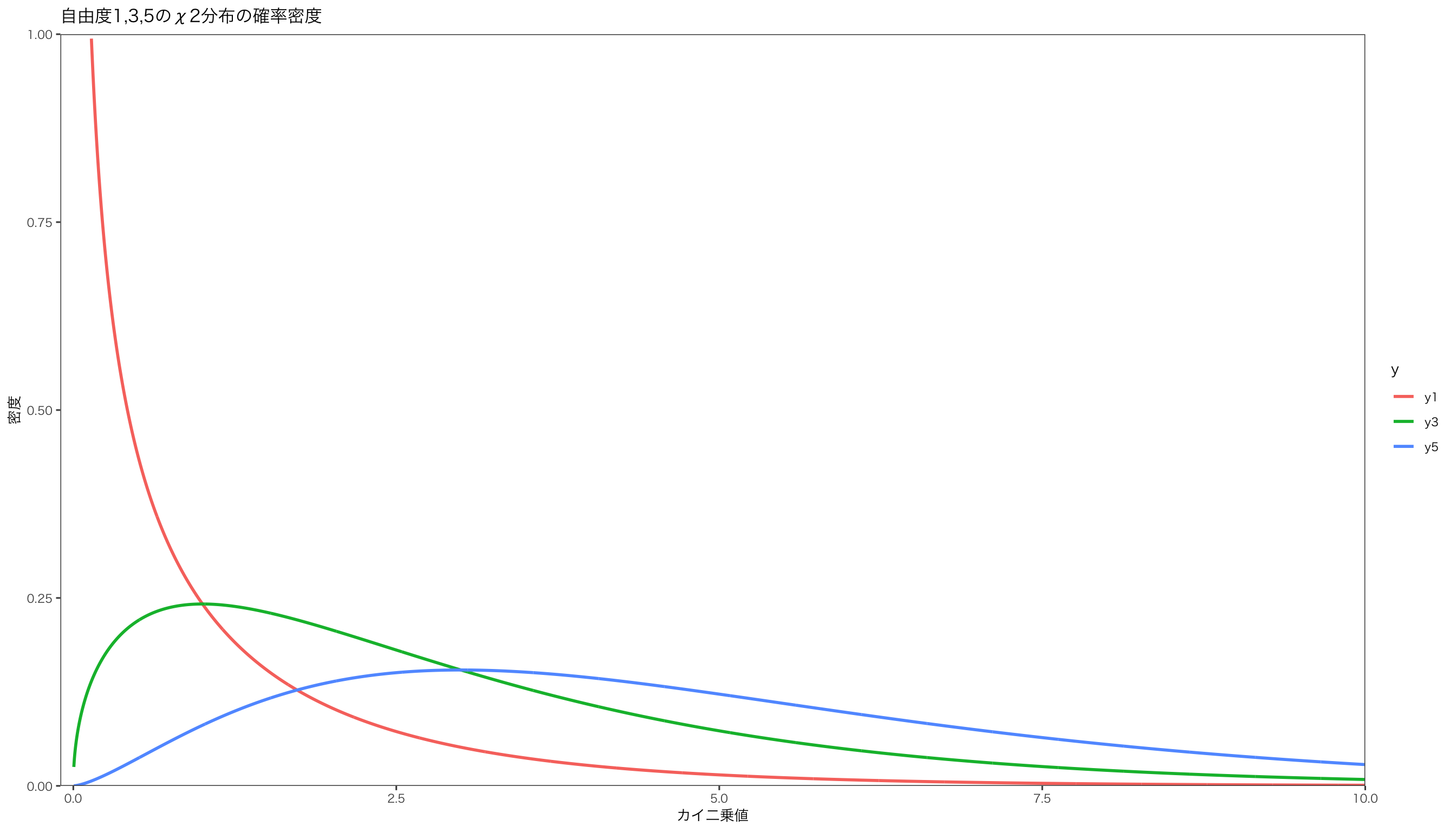
参考までに、自由度が変わると\(\chi^2\)分布の形状は次のようなものになります。

x = c(1:2500) / 250
y1 = dchisq(x,1) # 自由度1のカイ二乗分布の確率密度
y3 = dchisq(x,3) # 自由度3のカイ二乗分布の確率密度
y5 = dchisq(x,5) # 自由度5のカイ二乗分布の確率密度

df <- data.frame(x, y1, y3, y5) # データフレームを作成
df <- df %>%
  pivot_longer(names_to = "y",values_to = "value",cols = -x) # データを長く整形
p <- ggplot(df) + aes(x = x,y = value, group = y, color = y) # 作図
p <- p + geom_line(size = 1) # 折れ線グラフ
p <- p + ylim(c(0,1)) + ylab("密度") + xlab("カイ二乗値") +
  scale_y_continuous(expand = c(0,0), limits = c(0,1)) +
  scale_x_continuous(expand = c(0,0), limits = c(-0.1,10))
p <- p + ggtitle("自由度1,3,5のχ2分布の確率密度") +  mystyle
print(p)

自由度1の\(\chi^2\)分布における有意水準5%の値を調べるにはqchisq()関数を使います。引数は、pに確率、dfに自由度を指定します。

alpha <- 0.05  # 有意水準（ここでは5%）
df <- 1        # 自由度
qchisq(1 - alpha, df)

[1] 3.841459

自由度1のカイ二乗分布における有意水準5%の値は3.84であることが分かりました。 この値を超えると、有意水準5%で帰無仮説を棄却することになります。

では先程計算した\(\chi^2\)統計量は、有意水準5%で帰無仮説を棄却するかどうかを調べてみましょう。

chi2 <- 7.2
qchisq(1 - alpha, df) < chi2

[1] TRUE

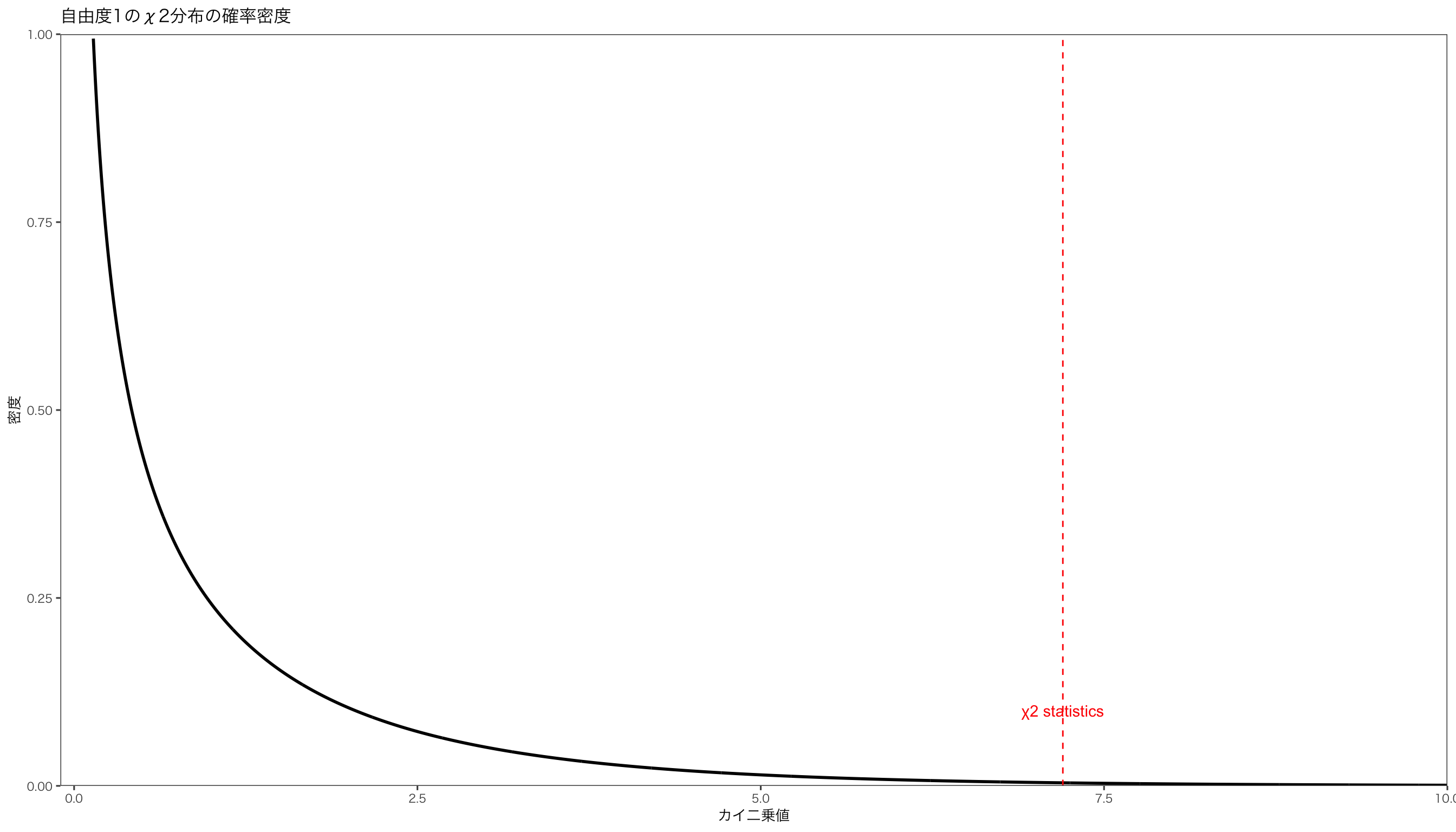
より、\(\chi^2\)統計量は有意水準5%で帰無仮説を棄却することが分かりました。 ちなみに、自由度1のカイ二乗分布の確率密度関数と\(\chi^2\)統計量の位置を重ねてみると次のようになります。

df <- data.frame(x,y1)
p <- ggplot(df) + aes(x = x,y = y1)
p <- p + geom_line(size = 1)
p <- p + ylim(c(0,1)) + ylab("密度") + xlab("カイ二乗値") +
  scale_y_continuous(expand = c(0,0), limits = c(0,1)) +
  scale_x_continuous(expand = c(0,0), limits = c(-0.1,10))
p <- p + ggtitle("自由度1のχ2分布の確率密度") +  mystyle
p <- p + geom_vline(xintercept = chi2, linetype = "dashed", color = "red")
p <- p + annotate("text", x = chi2, y = 0.1, label = "χ2 statistics", color = "red")
print(p)

このように、\(\chi^2\)統計量は、自由度1のカイ二乗分布のもとで生じる確率は、

1 - pchisq(chi2, df = 1)

[1] 0.007290358

となり、非常に小さな値であることが分かりました。 つまり、2つのカテゴリー変数の間に関係がない、という帰無仮説の下で、観測された度数が発生することはほぼありえない、ということが言えるので、帰無仮説は棄却され、2つのカテゴリー変数には関係があると結論付けられます。

Rでχ2検定

Rではchisq.test()関数を使ってχ2検定を行うことができます。 引数は、xに度数表、correctに補正を行うかどうか、pに期待度数を指定します。

先ほどの男女とメガネの例をここでも使ってみます。 まずmatrix()関数を使ってクロス集計表を行列として作成します。

O <- matrix(c(41, 81, 204, 74), nrow = 2, ncol = 2)
row.names(O) <- c("男性", "女性")
colnames(O) <- c("メガネ", "メガネなし")

E <- matrix(c(
  sum(O[,1])*sum(O[1,])/sum(O), #男眼鏡
  sum(O[,1])*sum(O[2,])/sum(O), #男眼鏡無
  sum(O[,2])*sum(O[1,])/sum(O), #女眼鏡
  sum(O[,2])*sum(O[2,])/sum(O)  #女眼鏡無
), nrow = 2, ncol = 2)

print(O)

     メガネ メガネなし
男性     41        204
女性     81         74

print(E)

       [,1]    [,2]
[1,] 74.725 170.275
[2,] 47.275 107.725

この観察度数と期待度数から、定義通りに\(\chi^2\)統計量を計算してみます。

chi <-  ((O[1,1] - E[1,1])^2 / E[1,1]) + #男眼鏡
        ((O[1,2] - E[1,2])^2 / E[1,2]) + #男眼鏡無
        ((O[2,1] - E[2,1])^2 / E[2,1]) + #女眼鏡
        ((O[2,2] - E[2,2])^2 / E[2,2])   #女眼鏡無
print(chi)

[1] 56.51731

\(\chi^2\) 統計量が 56.5173098 となりました。 この \(\chi^2\) 統計量が自由度1の \(\chi^2\) 分布にしたがう場合，この統計量が得られる確率は次のようになります。

prop <- 1 - pchisq(chi, df = 1)
print(prop)

[1] 5.57332e-14

この確率は0.0000000000000055733となり，ほぼゼロであることが分かりました。 よって、2つのカテゴリー変数は無関係である，という帰無仮説は棄却され、2つのカテゴリー変数には関係があると結論付けられます。

ちなみに，上記のようなめんどくさい処理をしなくても，Rにはchisq.test()という関数が用意されています。 chisq.test()は引数として、xに度数表、correctに補正を行うかどうか、pに期待度数を指定します。 補正は行わないので，correctはFALSEとします。 pはデフォルトで等確率となっているので，今回は省略します。

chisq.test(O, correct = FALSE)

    Pearson's Chi-squared test

data:  O
X-squared = 56.517, df = 1, p-value = 5.571e-14

となり，先ほどの結果と一致しました。

各マスに入る度数が少ない場合には、フィッシャーの直接確率検定を使います。

fisher.test(O)

    Fisher's Exact Test for Count Data

data:  O
p-value = 1.204e-13
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
 0.1127341 0.2982245
sample estimates:
odds ratio 
 0.1845096 

カイ二乗分布(補足)

カイ二乗分布は、確率変数\(Z_1, Z_2,\dots, Z_k\)が互いに独立であり、それぞれが標準正規分布\(N(0,1)\)に従うとき、その二乗和が従う分布を自由度\(k\)のカイ二乗分布といいます。

\[ \chi^2 = Z_1^2 + Z_2^2 + \dots + Z_k^2 \]

導出は省きますが、自由度\(k\)のカイ二乗分布の密度関数は、

\[ \begin{aligned} f(x) = \begin{cases} \frac{1}{2^{k/2} \Gamma(k/2)} x^{k/2 - 1} \mathrm{e}^{-x/2} & (x \geq 0)\\ 0 & (x < 0) \end{cases} \end{aligned} \]

ここで、\(\Gamma\)はガンマ関数であり、

\[ \Gamma \left (\frac n2 \right) = \int_0^{\infty} t^{k/2 - 1} \mathrm{e}^{-t} \mathrm{d}t \] となります。

導出は省きますが、カイ二乗分布の期待値は\(k\)となり、分散は\(2k\)となります。

量的変数間の関係

ここでは、2つ以上の量的変数間の関係を調べる方法について学びます。 具体的には、相関係数と散布図について学習します。

相関関係の種類・散布図・相関係数

2つの量的変数(連続変数)が同時に変化する関係を相関関係(correlation)といいます。 相関関係には、

• 正の相関(positive correlation)
• 負の相関(negative correlation)
• 無相関(no correlation)

の3種類があります。

まずは，2つの量的変数を使って散布図(scatter diagram)を描いて，目で見て相関関係があるかどうかを判断します。 そして，相関係数(correlation coefficient)を計算して，数値的に相関関係があるかどうかを判断します。 相関係数は次のように計算されます。

\[ r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \]

分子は、\(x\)と\(y\)の共分散(covariance)で、分母は\(x\)の標準偏差と\(y\)の標準偏差の積です。 相関係数\(r\)は\(-1\)から\(1\)の値をとります。 \(r\)が\(1\)に近いほど正の相関が強く、\(-1\)に近いほど負の相関が強く、\(0\)に近いほど無相関になります。

相関係数が\(-1\)から\(1\)の値をとることを証明することは簡単なのですが，それを書くには余白が足りないので，ここには示しません。 コーシー・シュワルツの不等式を使うか，\(x\)と\(y\)の偏差のベクトルの角度が\(\cos\)であることを示すか，のどちらかで証明できます。

相関係数を使った統計的仮説検定

相関係数が同じでも統計的に有意になるか否かは、標本サイズで決まるということを教科書で理解しておきましょう。

Rでやってみる

母平均\(0\)、母標準偏差\(1\)の正規分布にしたがう変数\(X\)と\(Y\)を考えます。 母集団のサイズは10000とします。

N <- 10000 # 母集団のサイズ
X <- rnorm(N, 0, 1) # 平均0，標準偏差1の正規分布からN個
Y <- rnorm(N, 0, 1) # 平均0，標準偏差1の正規分布からN個
P <- data.frame(X,Y) # データフレームを作成
ggplot(P) + aes(X,Y) + # グラフの下地
  geom_point() + # 散布図
  ggtitle("母集団") + mystyle # タイトルとスタイル

この母集団から標本サイズ100の標本を100個とりだし、相関係数を100個計算します。

n <- 100 # 標本サイズ
trial <- 100 # 試行回数
sig <- numeric(n) # 空の入れ物
cor <- numeric(n) # 空の入れ物
for(i in 1:trial){ # ループ
  x_sample <- sample(X, n) # 母集団からn個の標本を取り出す
  y_sample <- sample(Y, n) # 母集団からn個の標本を取り出す
  res <- cor.test(x_sample, y_sample) # 相関係数を計算
  sig[i] <- res$p.value # p値
  cor[i] <- cor(x_sample, y_sample) # 相関係数
}
df_cor <- data.frame(cor,sig) # p値と相関係数をデータフレームにまとめる
df_cor %>% arrange(sig) %>% head() # p値で並び替えて上位5つを表示

cor	sig
0.3032027	0.0021663
-0.2678916	0.0070457
-0.2637771	0.0080077
-0.2509923	0.0117747
0.2344974	0.0188575
-0.2343658	0.0189263

たとえば、ある標本の散布図はこうなります。

x_sample <- sample(X, n) # 母集団Xからn個の標本を取り出す
y_sample <- sample(Y, n) # 母集団Yからn個の標本を取り出す
data.frame(x_sample, y_sample) %>% # データフレームにまとめる
    ggplot() + aes(x_sample, y_sample) + # グラフの下地
    geom_point() + # 散布図
    geom_smooth(method = "lm", se = FALSE) + # 回帰直線
    ggtitle("標本") + mystyle # タイトルとスタイル

微妙に右肩上がりの関係がありそうですが、ほぼ無相関といえるでしょう。 では、100個の標本から計算した100個の相関係数の大きさを並べてみましょう。 変数を並び替えるには，dplyrのarrange()関数を使います。 デフォルトでは昇順に並び替えられますが，arrange(desc())とすることで降順に並び替えることができます。

無相関となる母集団からの標本を100個とっているので、標本の相関係数も0に近い値となることが予想されますが、いくつかの標本では\(-0.3\)や\(0.2\)といった相関があるという結果が得られています。

以下のコードで、相関係数の値が小さい順に並べています。 ggplotのaes()の中で、reorder()関数を使って、seq_along(cor)をcorの値で並び替えています。 reorder()関数は第一引数の数列を第二引数の数列の値で並び替える関数です。 seq_along(cor)は1,2,3,...,100という数列を作成し，reorder()関数で第一引数の数列を第二引数の数列の値で並び替えています。 geom_barの引数の中のfillは棒グラフの色を指定しているのですが，ここにifelse()関数を使うことで，sigの値が0.05より小さい場合は赤色，そうでない場合は黒色になるようにしています。

ggplot(data.frame(df_cor)) +
    aes(x = reorder(seq_along(cor), cor), y = cor) +
    geom_bar(stat = "identity", fill = ifelse(sig < 0.05, "red", "black")) +
    ylab("相関係数") + xlab("標本ID") + ggtitle("相関係数の分布") + mystyle

では、それらの値が、母集団では相関係数が\(0\)であるという帰無仮説が正しいとした場合に、どのくらいの確率で得られるのかを調べてみましょう。

ggplot(data.frame(df_cor)) +
    aes(x = reorder(seq_along(sig), sig), y=sig) + # データの指定
    geom_bar(stat="identity", fill = ifelse(sig < 0.05, "red", "black")) + # 棒グラフ
    ylab("p値") + xlab("標本ID") + ggtitle("相関係数のp値の分布") + mystyle # 軸ラベルとタイトル

相関係数が0である母集団から標本を抜き出して、その標本相関係数の値が0.3となる確率\(p\)値は0.002となりました。 もし自分がもっている広告費と売上高のデータから相関係数を計算し、その値が0.3であったなら、母集団では相関係数が\(0\)であるという帰無仮説の下では、ほとんど起こりえないことが起こったということになります。 この場合、帰無仮説が間違っていて、対立仮説である広告費と売上高には関係があるという仮説のほうがもっともらしい、ということになります。 逆に、帰無仮説を棄却できなかった場合、広告費と売上高の間に関係は無いと主張することはできません。 帰無仮説が棄却できなかった場合は、関係があるかどうかはわからないということになります。

相関関係と因果関係

重要

相関関係があるからといって、必ずしも因果関係があるとは限らない。

広告費と売上高の関係について考えてみましょう。

因果関係

可能性1：広告費が売上高に影響を与えている、という関係を想定しています。

graph LR
    A[広告費] --> B[売上高]

因果関係

可能性2：売上高が広告費に影響を与えている、という関係を想定しています。

graph RL
    B[売上高] --> A[広告費]

互恵関係

可能性3 : 可能性1と可能性2が同時に起こっている、という関係を想定しています。

graph LR
    A[広告費] --> B[売上高]
    B[売上高] --> A[広告費]

見せかけの相関

広告費と売上高の両方に影響を与える第3の要因が存在する場合、広告費と売上高の間に相関関係があるように見える、という想定です。 ここでは、広告費と売上高の両方に影響を与える第3の要因として、内部資金を想定しています。内部資金が潤沢な会社は、広告宣伝費も増加させることができるし、売上高も増加させることができる、という想定です。

graph TB
    A[内部資金] --> B[広告費]
    A[内部資金] --> C[売上高]

graph TB
    A[内部資金] --> B[広告費]
    A --> C[売上高]
    B -.-> C