統計的仮説検定

第7回講義の到達目標は、

  • 統計的検定の基礎を理解し，説明することができる。
  • 帰無仮説と対立仮説を理解し，説明することができる。
  • 第1種の過誤と第2種の過誤を理解し，説明することができる。

第7回講義の到達度検証のための課題は、以下の通りです。

  • 統計的仮説を立てることができる。
  • 第1種の過誤と第2種の過誤を解釈する

準備

# 文字化け防止のおまじない、R 4.1.0以降
knitr::opts_chunk$set(dev = "ragg_png")

library(tidyverse) # とりあえずこれ
library(ggthemes) # ggplot2のテーマ
library(knitr)
library(kableExtra)
library(gghighlight)

# テーマを設定
theme_set(theme_few(base_size = 12))
# 以下、ggplot2のデフォルトを変更
update_geom_defaults("point", list(size = 3))

第8章「統計的仮説検定」は統計学における最重要学習内容の「検定」について学びます。 検定は、母集団の母数(パラメータ)に関する仮説を立てて、その仮説が正しいかどうかを検証する方法です。 統計学は、観察できない未知の母数をもつ母集団から標本を抽出し、標本の特徴をもとに母集団の母数を推定することを目的としています。 そのため、自分の手元にある標本が、母集団の母数を推定するための有効な情報をもっているかどうかを検証する必要があります。

テレビCMを流せば本当に売上が上がるのか、を調べたいと思い、標本を集めて分析しようとし、その結果、テレビCMを流すと売上が上がるという結果が出たとします。 しかし、この結果が、本当は母集団ではCMと売上高は無関係であるのに、たまたま集めた標本で関係があるように見えているだけなのか、それとも母集団でもCMと売上高は関係があるのか、を検証する必要があります。 統計的仮説検定は、(頻度主義)統計学で最も重要なものですので、何度も読んで理解し、そして使いこなせるようになってください。

統計的仮説検定の基礎

母集団の母数(パラメータ)を知りたいけれど観察できないので、母集団から標本(sample)を抽出して、標本の特徴をつかって母集団の母数を予想しようとすることを、統計的推定(statistical estimation)といいます。

この章では、母数に対して立てた仮説が妥当かどうかを検証する方法を学びます。

  1. 仮説をたてる
  2. 有意水準を設定する
  3. 検定統計量を計算する
  4. 検定統計量の確率分布を求めて有意水準で棄却域を決める
  5. 検定統計量が棄却域に入るかどうかを確認する

仮説の立て方：帰無仮説と対立仮説

仮説の立て方は、帰無仮説(null hypothesis)と対立仮説(alternative hypothesis)の2つに分けられます。 (頻度主義)統計学では、本当に示したい仮説(対立仮説)ではなく、その排反事象である帰無仮説を立てて、帰無仮説が棄却されることで、対立仮説が採択されるという考え方をとります。 排反事象(incompatible events)とは、同時に起こりえない事象のことです。

例えば、

  • 帰無仮説\(H_0\) : 利益反応係数\(ERC\)はゼロである。　\(ERC =0\)
  • 対立仮説\(H_A\) : 利益反応係数$\(ERC\)はゼロではない。 \(ERC \not = 0\)

というように、帰無仮説は対立仮説と背反となるように立てます。 また、帰無仮説は母数に対して等号で成立する仮説となります。 なぜこんなことをするのかというと、母数がある特定の値をとる、という帰無仮説を否定するためには、その値以外の取りうることを示せばよいだけですが、もし対立仮説が\(ERC=0\)であったなら、これを示すためには、\(ERC \not = 0\)を示す必要があります。 これは不可能です。

有意水準の設定

次に、どんなときに帰無仮説を棄却するのかを決めます。 帰無仮説として仮定した母数の値から標本から計算した値が大きく異なる場合には、帰無仮説を棄却する、とします。 このとき、どのくらい帰無仮説として仮定した母数の値から離れたら帰無仮説を棄却するのかを決めるのが有意水準(significance level)です。優位水準と書かないように気をつけましょう。

有意水準は、\(\alpha\)で表され、会計研究では\(0.01\)、\(0.05\)、\(0.10\)が使われることが多いです。 標本サイズが大きい場合だと、\(0.001\)とか\(0.005\)とかも使われます。

例えば、母集団の平均\(\mu\)が\(0\)である、という帰無仮説を考えます。このとき対立仮説は母集団の平均\(\mu\)は\(0\)ではない、というものです。 標本サイズ\(100\)の標本から抽出した標本平均の分布から計算した\(t\)値が自由度\(100-1\)の\(t\)分布にしたがうとき、

\[ t = \frac{\bar{x} - \mu}{s/\sqrt{n}} \] となり，今\(\bar{x} = \mu\)という帰無仮説を仮定しているので、\(t = 0\)となります。

# 自由度を設定
n = 100
df <- n-1

# データを生成
data <- data.frame(x = seq(-5, 5, by = 0.01))
data$y <- dt(data$x, df) # 変数yを作成


# 90%の領域の上限と下限をqt()で計算
ql <- qt(0.025, df)
qu <- qt(0.975, df)

# t分布を書く
g <- ggplot(data) + aes(x = x, y = y) + geom_line()
g <- g + geom_area(data = data %>% filter(x <= ql), fill = "blue", alpha = 0.3) + geom_area(data = data %>% filter(x >= qu), fill = "blue", alpha = 0.3)
g <- g + geom_vline(xintercept = 0, color = "red")
g <- g + xlab("t値") + ylab("確率密度") + labs(title = "90%の確率で起こるt値の範囲")
g <- g + geom_hline(yintercept = 0)
g <- g + annotate(geom = "text", x = 2.4, y = 0.08, label = "α/2", size = 10)
g <- g + annotate(# 始点や終点などを指定して矢印を追加
  geom = "segment", x = 2.4, xend = 2.2,
  y = 0.07, yend = 0.04, color = "black", size = 0.5,
  arrow = arrow(length = unit(0.3, "cm"))
  )
g <- g + annotate(geom = "text", x = -2.4, y = 0.08, label = "α/2", size = 10) +
  annotate(# 始点や終点などを指定して矢印を追加
  geom = "segment", x = -2.4, xend = -2.2,
  y = 0.07, yend = 0.04, color = "black", size = 0.5,
  arrow = arrow(length = unit(0.3, "cm"))
  )
print(g)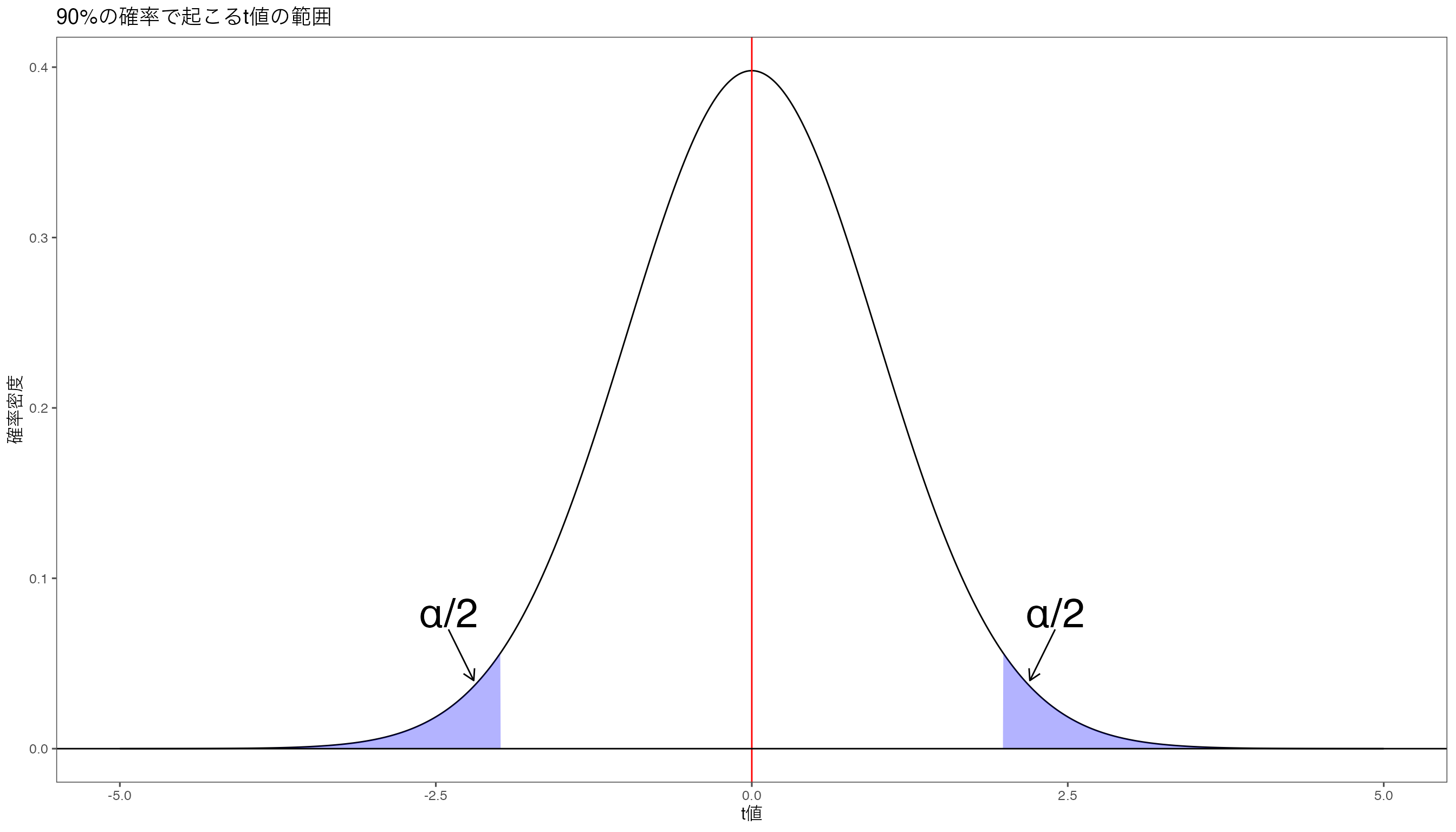

検定統計量の計算

標本から平均などの統計量を計算し，その統計量は確率変数なので分布をもち，その分布 \[ \begin{align*} t = \frac{\bar{x} - \mu}{SE} = \displaystyle \frac{\bar{x} - \mu}{\frac{u}{\sqrt{n}}} \end{align*} \] を検定統計量

Rでやってみる

母平均\(62\)、母標準偏差\(5\)の正規分布にしたがう変数\(X\)を考えます。 母集団のサイズは10000とします。 この母集団の分布は次のようになっています。

N <- 10000
X <- rnorm(N, 62, 5) # 母集団
ggplot(data.frame(X)) + aes(X) + geom_histogram() + ggtitle("母集団") + geom_vline(xintercept = 62, color = "red")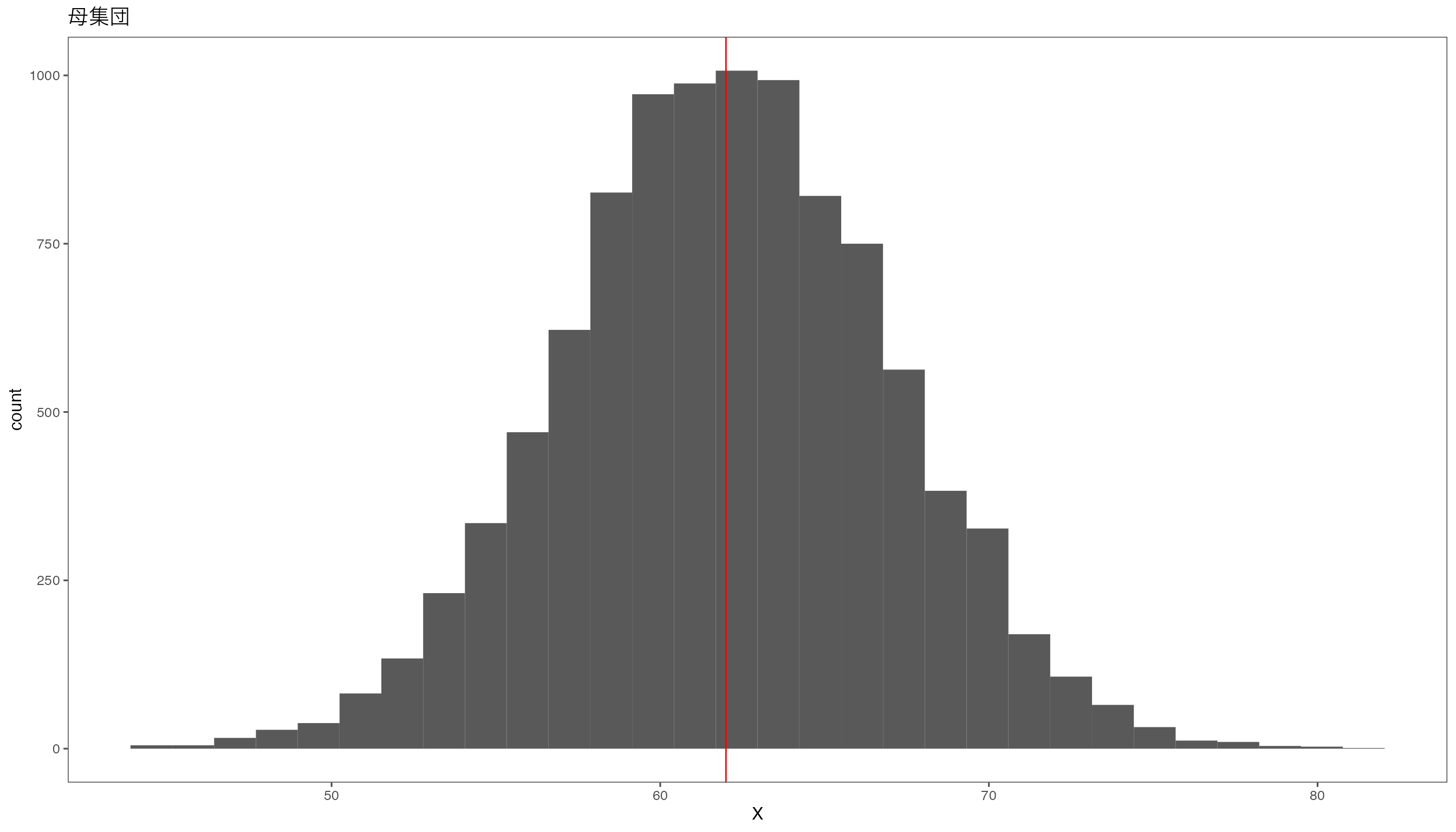

この母集団から標本サイズ100の標本を100個とりだし、平均を100個計算します。

n <- 100
sample_mean <- numeric(n) # 空の箱を用意
for(i in 1:100){
  x_sample <- sample(X, n) # 標本を抽出
  sample_mean[i] <- mean(x_sample) # 標本平均を計算
}
df_mean <- data.frame(sample_mean)

たとえば、ある標本の平均値は62.39はこうなります。

この平均値がどのように分布しているのかを調べるために、ヒストグラムを作成してみます。

g_mean <- ggplot(df_mean) + aes(x=sample_mean) +
  geom_histogram() + xlab("標本平均") + ylab("度数") +
  geom_vline(xintercept = mean(sample_mean), color = "blue") +
  geom_vline(xintercept = 62, color="red")
print(g_mean)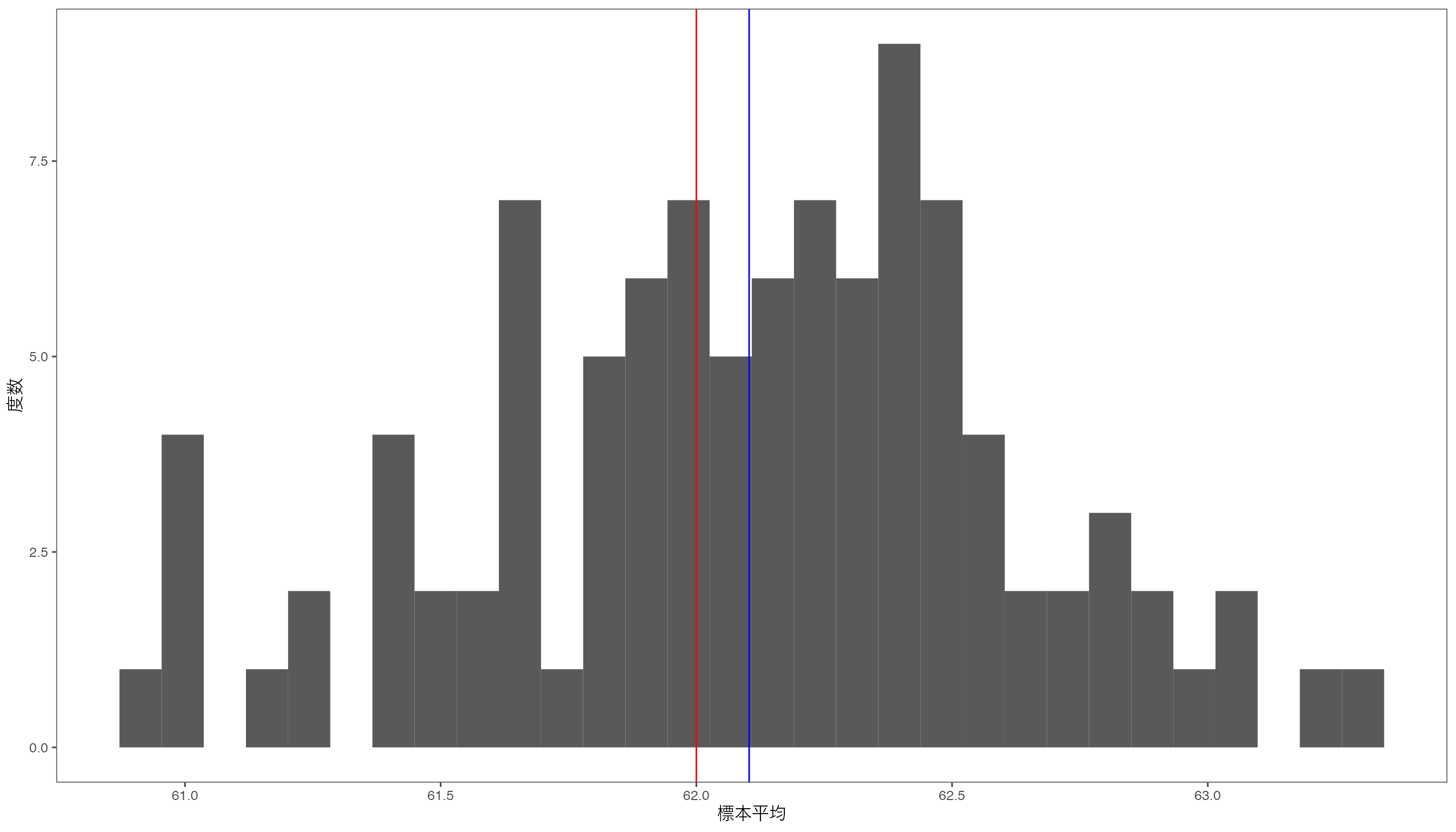

g_m <- ggplot(df_mean) +
    aes(x = reorder(seq_along(sample_mean), sample_mean), y = sample_mean) +
    geom_bar(stat="identity") + geom_hline(yintercept = 62, color = "red") +
   coord_cartesian(ylim = c(60, 64)) +
    ylab("標本平均") + xlab("標本ID") + ggtitle("標本平均の分布")
print(g_m)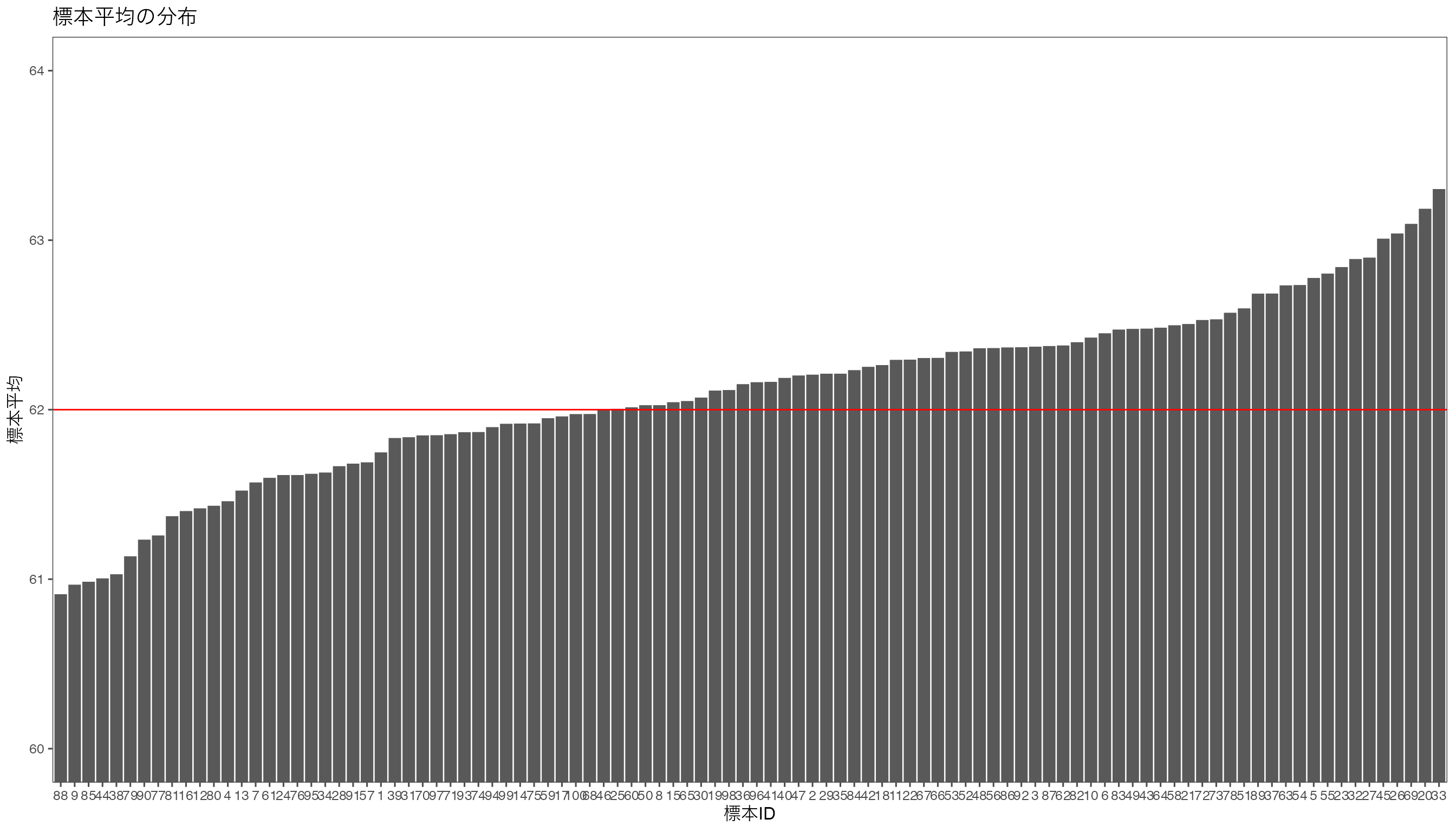

おおよそ母平均\(\mu = 62\)の周りに分布していることがわかりますが，かなり離れた標本平均をもつ標本もあるようです。 たとえば，100個の標本で最小の標本平均となった標本の平均は60.91です。 このように母平均62，母標準偏差5の母集団から抽出した1つの標本サイズ100の標本平均が，60.91という値になる確率はどのくらいでしょうか。 標本平均から\(t\)値を計算し，その\(t\)値が自由度99の\(t\)分布にしたがう確率を求めることで，この確率を求めることができます。

t <- (min(df_mean$sample_mean) - 62) / (5 / sqrt(n))
print(t)
[1] -2.177608

自由度99の\(t\)分布の下で，となる確率は求めると，

pt(t, df = n-1)
[1] 0.01590538

となり，この確率は非常に小さい値となります。 つまり100個の標本をとってくると，いくつかの標本から計算された標本平均は，母平均62からかなり離れた値となることがわかります。 それぞれの標本平均から計算された\(t\)値の分布を調べると，次のようになります。

df_mean <- df_mean %>%
  mutate(
    t_value = (sample_mean - 62) / (5 / sqrt(n)),
    p_value = pt(t_value, df = n-1)
  )

ggplot(df_mean) +
    aes(x = reorder(seq_along(p_value), p_value), y = p_value) + # グラフの設定
    geom_bar(stat="identity", fill = ifelse(df_mean$p_value < 0.05, "red", "black")) + #
    geom_hline(yintercept = 0.05, color = "red") + # 有意水準0.05
    ylab("p値") + xlab("標本ID") + ggtitle("p値の分布")  # 軸の設定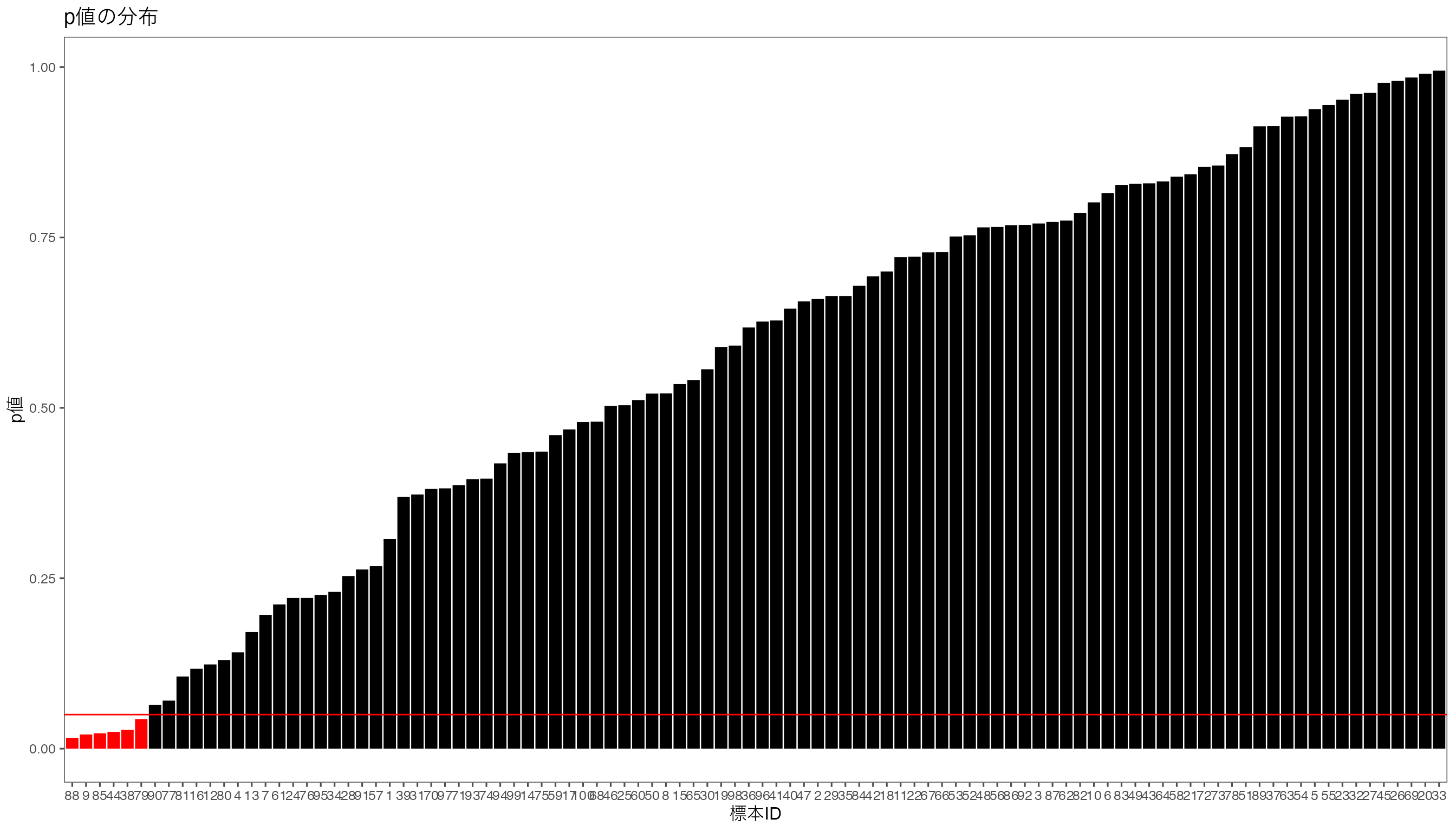

となり，\(t\)値が生じる確率が5%未満となる標本がいくつかあることがわかった。 自分が集めた標本の1つから計算した標本平均、そして\(t\)値が、帰無仮説が正しいと仮定した場合に、その標本平均がどのくらいの確率で生じるかを調べ、それが5%未満や1%未満であったならば、帰無仮説が正しいと考えるよりも、帰無仮説とは異なる母平均をもつ母集団から標本を集めたから、そのような標本平均が生じたと考えるほうがもっともらしいと考えることができます。 これが統計的仮説検定の考え方です。

統計的検定の諸問題

仮説検定における2種類の「誤り」と検出力

  • 第1種の過誤(type 1 error) : 帰無仮説が正しいのに，帰無仮説を棄却してしまう誤り。偽陽性(False Positive)とも呼ばれる。
  • 第2種の過誤(type 2 error) : 帰無仮説が正しくないのに，帰無仮説を棄却しない誤り。偽陰性（False Negative）とも呼ばれる。

第1種の過誤の例として，よく挙げられる犯罪容疑者の例で説明すると，容疑者が無実なのに，容疑者を有罪としてしまう(えん罪)誤りを第1種の過誤といい，容疑者が犯罪者なのに，容疑者を無罪としてしまう誤りを第2種の過誤といいます。

第1種の過誤(えん罪)を小さくしたいとします。 この確率を$$で表し，実はこれが有意水準の大きさとなります。 有意水準5％というのは，ある検定統計量の標本分布の平均から離れた5％の面積に入る統計量をかけ離れた値とするかを(研究者が勝手に)決めたものです。 両側検定なら，標本平均から離れた左右の2.5％の面積に入る統計量をかけ離れた値とし，ここに計算した統計量が含まれるとき，帰無仮説を棄却します。

第1種の過誤と減らすために有意水準を小さくすると，だい2種の過誤が大きくなります。 当然ですが，えん罪を減らそうとしてほとんどのケースを無罪とすると，犯罪者を逃がすことになる，というロジックと同じです。

帰無仮説が正しいとした場合の正規分布を青色で，真の分布を赤色で示し，有意水準が両側で5％，つまり片側が2.5％となる図を書くとこんな感じです。

# 正規分布の確率密度関数
dnorm_with_mean_sd <- function(x, mean = 0, sd = 1) {
  sqrt(1/(2*pi*sd^2))*exp(-((x - mean)^2)/(2*sd^2))
}

# パラメータの設定
mu1 <- 0   # 帰無仮説の平均
sd1 <- 1   # 帰無仮説の標準偏差
mu2 <- 1.5 # 対立仮説の平均
sd2 <- 1   # 対立仮説の標準偏差
alpha = 0.025

# サンプルデータを生成
x <- seq(-5, 5, by = 0.01)
df <- data.frame(x = x,
                 dnorm1 = dnorm_with_mean_sd(x, mean = mu1, sd = sd1),
                 dnorm2 = dnorm_with_mean_sd(x, mean = mu2, sd = sd2))

# ggplotを使って描画
g <- ggplot(df, aes(x = x)) +
  geom_line(aes(y = dnorm1), color = "blue") +
  geom_line(aes(y = dnorm2), color = "red")
g <- g + geom_area(
  data = subset(df, x > qnorm(1-alpha, mu1, sd1)),
            aes(y = dnorm1), fill = "blue", alpha = 0.2)
g <- g + geom_area(
  data = subset(df, x < qnorm(alpha, mu1, sd1)),
  aes(y = dnorm1), fill = "blue", alpha = 0.2)
g <- g + geom_area(
  data = subset(df, x > qnorm(alpha, mu1, sd1) & x < qnorm(1-alpha, mu1, sd1)),
            aes(y = dnorm2), fill = "red", alpha = 0.2) +
  theme_minimal() +
  labs(x = "Value", y = "Density",
       title = "両側検定における第1種の過誤と第2種の過誤")
g <- g + geom_vline(xintercept = qnorm(1-alpha), linetype="dotted")
g <- g + geom_vline(xintercept = mu1, color = "darkblue")
g <- g + geom_vline(xintercept = mu2, color = "darkred")

g <- g + annotate("text", x = mu1 + 2.5, y = max(df$dnorm1) / 6,
           label = "第1種の過誤", color = "darkblue", family = "HiraKakuProN-W3") +
  annotate("text", x = mu2 - 0.5, y = max(df$dnorm2) / 6,
           label = "第2種の過誤", color = "darkred", family = "HiraKakuProN-W3")

g <- g + annotate("text", x = mu1 - 2, y = max(df$dnorm1)-0.1,
                  label = "帰無仮説下の分布", color = "blue", family = "HiraKakuProN-W3" ) +
  annotate("text", x = mu2 + 1.5, y = max(df$dnorm2) - 0.1,
           label = "真の分布", color = "red", family = "HiraKakuProN-W3")
print(g)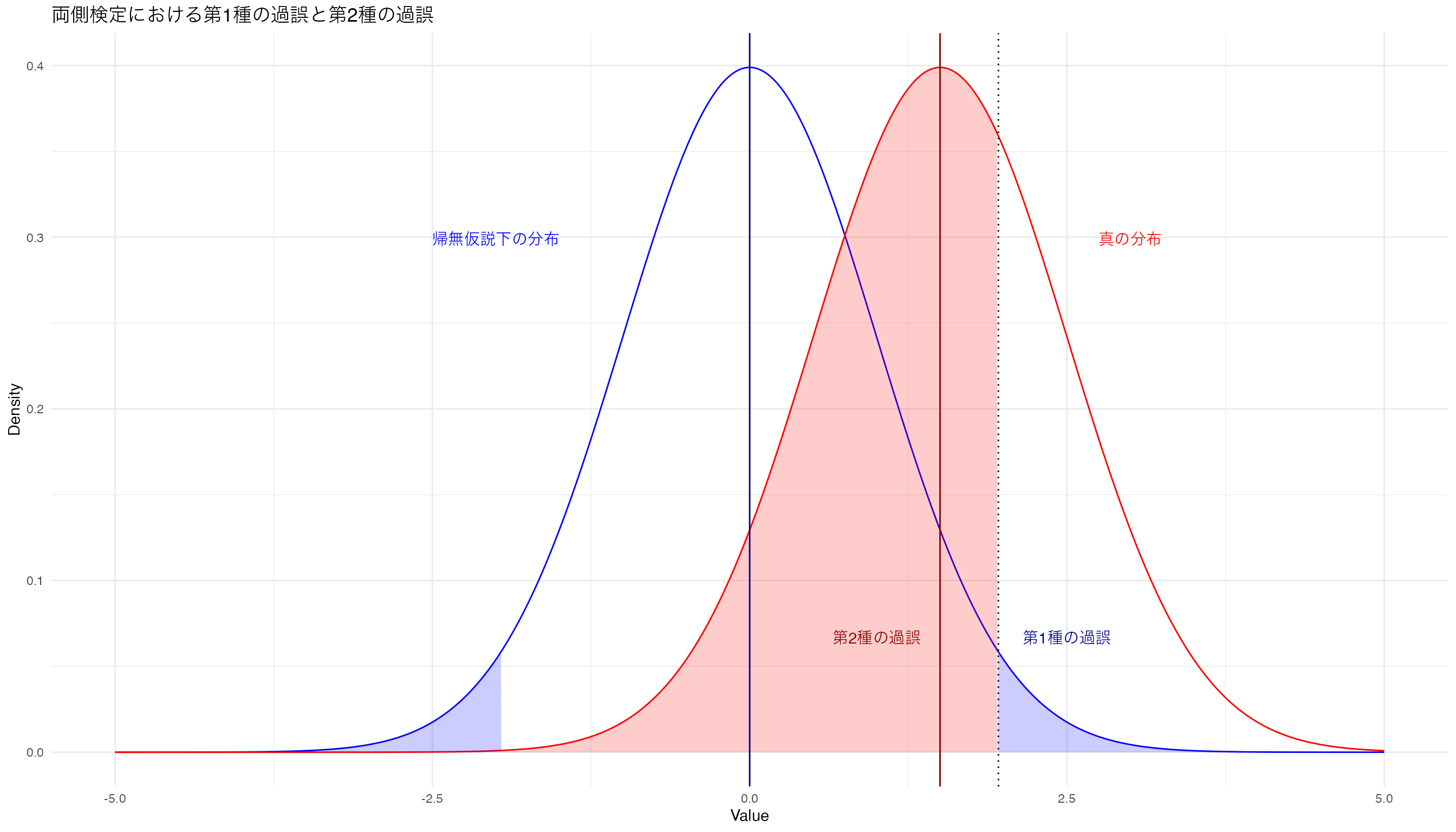

帰無仮説が正しいときに帰無仮説を棄却する確率である第1種の過誤\(\alpha\)を小さくすると，こうなります。

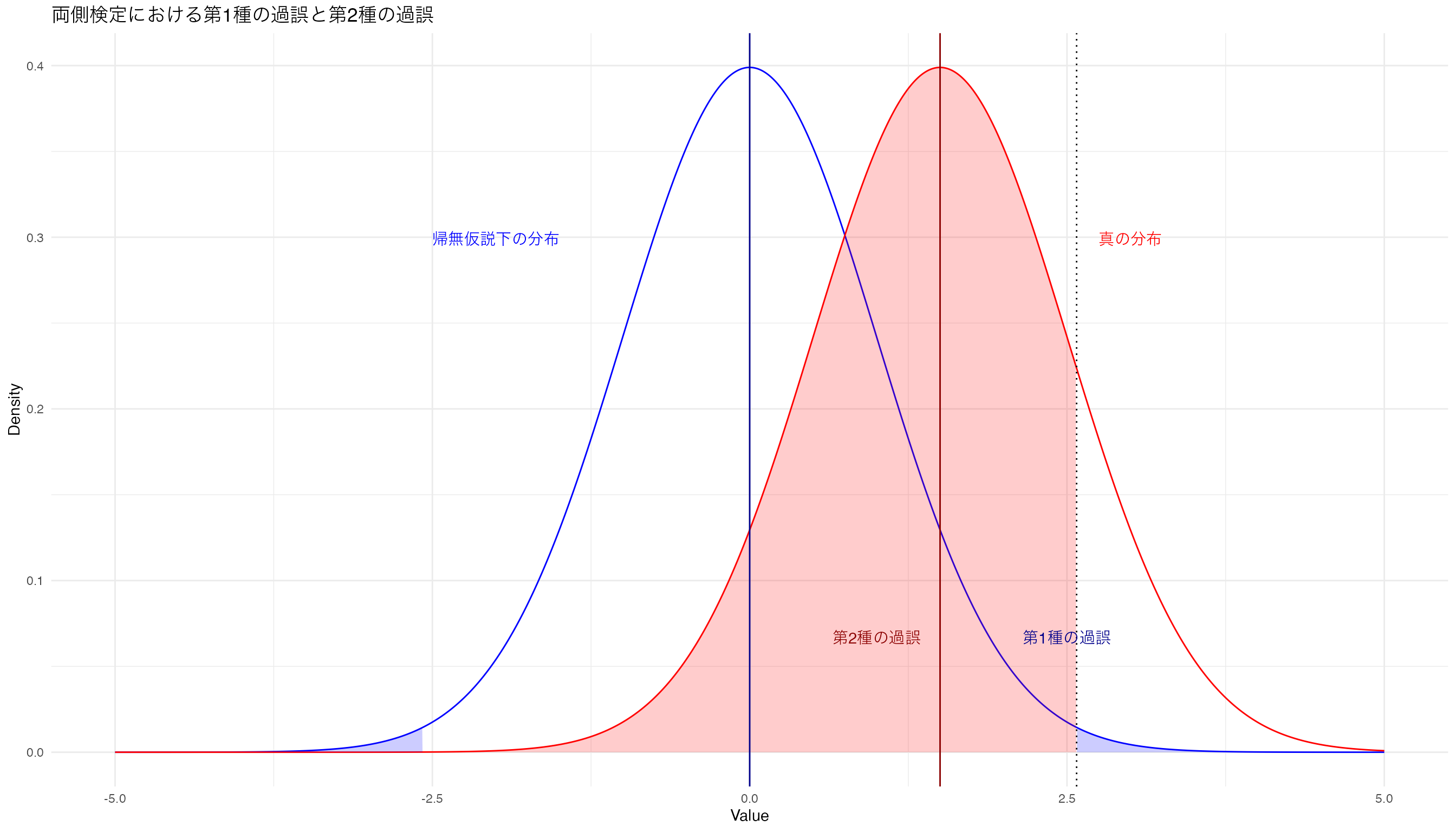
片側検定の場合なら，こんな感じです。