pacman::p_load(tidyverse, readxl, arules, ggthemes, knitr, kableExtra, gt, gtExtras, patchwork)5 第5回 併売の分析
5.1 はじめに
パッケージとデータを準備する。
第3回ファイルで使うデータはchp5.xlsxです。
chp5.xlsx
パッケージを読み込みます。
ここで用いるchp5.xlsxのシート名を確認します。
readxl::excel_sheets("data/chp5.xlsx")[1] "いつものPOSデータ" "ピボットテーブル" "図5-2・表5-1"
[4] "図5-3" "表5-2" "表5-3・表5-4"
[7] "併売データ" "表5-6・表5-7" 5.2 併売の基礎集計
最初の分析では、併売の基礎集計を行うために、1番目のシート「いつものPOSデータ」を読み込みます。
df <- readxl::read_excel("data/chp5.xlsx", sheet = 1)
head(df)| レシート番号 | 日付 | 曜日 | 時間 | 性別 | 年代 | メーカー | 商品名 | 単価 | 個数 | 金額 |
|---|---|---|---|---|---|---|---|---|---|---|
| R000001 | 2023-01-02 | 月 | 10 | 女性 | 30代 | 競合A | おいしい緑茶 | 160 | 2 | 320 |
| R000001 | 2023-01-02 | 月 | 10 | 女性 | 30代 | 競合B | 静岡の緑茶 | 170 | 2 | 340 |
| R000002 | 2023-01-02 | 月 | 10 | 男性 | 60歳以上 | 競合A | おいしい濃茶 | 160 | 2 | 320 |
| R000002 | 2023-01-02 | 月 | 10 | 男性 | 60歳以上 | 競合B | 静岡の緑茶 | 170 | 4 | 680 |
| R000003 | 2023-01-02 | 月 | 10 | 男性 | 50代 | 競合C | ほうじ茶 | 140 | 1 | 140 |
| R000004 | 2023-01-02 | 月 | 10 | 女性 | 50代 | 競合D | ウーロン茶 | 140 | 3 | 420 |
まず,各商品が購入された回数を示すように,個数が1以上のとき1を,そうでないときに0を返すダミー変数を作成し,回数という変数とします。
df_wide <- df |>
select(レシート番号, 商品名, 個数) |> # 必要な列だけ抽出
mutate(回数 = if_else(個数 > 0, 1, 0)) |> # 個数が1以上の場合は1、それ以外は0
select(レシート番号, 商品名, 回数) |>
pivot_wider(names_from = 商品名, values_from = 回数, values_fill = 0)
head(df_wide)| レシート番号 | おいしい緑茶 | 静岡の緑茶 | おいしい濃茶 | ほうじ茶 | ウーロン茶 | 濃い茶 | 緑茶 |
|---|---|---|---|---|---|---|---|
| R000001 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| R000002 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| R000003 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| R000004 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| R000005 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| R000006 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
df |>
select(レシート番号, 商品名, 個数) |> # 必要な列だけ抽出
mutate(回数 = if_else(個数 > 0, 1, 0)) |> # 個数が1以上の場合は1、それ以外は0
group_by(商品名) |> # 商品ごとにグループ化
summarise(購入回数 = sum(回数)) |> # 購入回数を合計
arrange(desc(購入回数)) |> # 購入回数で降順ソート
gt() |> # 作表
fmt_number(columns = 2, decimals = 0) |>
tab_options(
heading.title.font.size = "normal",
table.font.size = "small"
) |>
gt_theme_pff()| 商品名 | 購入回数 |
|---|---|
| おいしい緑茶 | 84,832 |
| 緑茶 | 65,755 |
| おいしい濃茶 | 59,910 |
| 静岡の緑茶 | 46,516 |
| 濃い茶 | 45,982 |
| ほうじ茶 | 39,190 |
| ウーロン茶 | 31,905 |
これで、テキストの図5-1と同様に、レシート番号ごとに商品名が列になり、購入された場合に1、購入されなかった場合に0が入ったデータフレームができました。 図5−2と同じになるように、自社商品、競合A社〜D社という製品の並びに変更します。
df_wide <- df_wide |>
select(レシート番号, 緑茶, 濃い茶, おいしい緑茶, おいしい濃茶, 静岡の緑茶, ほうじ茶, ウーロン茶)
df_wide |> tail(4)| レシート番号 | 緑茶 | 濃い茶 | おいしい緑茶 | おいしい濃茶 | 静岡の緑茶 | ほうじ茶 | ウーロン茶 |
|---|---|---|---|---|---|---|---|
| R225613 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| R225614 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| R225615 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| R225616 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
ここから、各商品が別の各商品と一緒に購入された回数を集計します。 まずは自社製品の緑茶だけを取り出して、図5-3を再現してみます。
| レシート番号 | 緑茶 | 濃い茶 | おいしい緑茶 | おいしい濃茶 | 静岡の緑茶 | ほうじ茶 | ウーロン茶 |
|---|---|---|---|---|---|---|---|
| R000005 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| R000010 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| R000011 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| R000012 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| R000016 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
変数ごとの合計を求めることで、この緑茶と一緒に購入された回数を商品別に集計します。
df_wide |>
filter(緑茶 == 1) |> # 緑茶が購入された場合
select(-緑茶) |>
summarise(across(濃い茶:ウーロン茶, sum)) |> # 商品ごとに合計
gt() |> # 作表
fmt_number(columns = 1:6, decimals = 0) |>
tab_options(
table.font.size = "small"
) |>
tab_header(title = "緑茶と一緒に購入された商品の個数") |>
gt_theme_pff()| 緑茶と一緒に購入された商品の個数 | |||||
|---|---|---|---|---|---|
| 濃い茶 | おいしい緑茶 | おいしい濃茶 | 静岡の緑茶 | ほうじ茶 | ウーロン茶 |
| 11,426 | 15,441 | 10,835 | 9,737 | 8,149 | 6,668 |
これを関数にして、他の商品にも適用し、一緒に購入された回数を集計します。
# 全商品名を取得
product_names <- colnames(df_wide)[-1] # レシート番号以外の列
# 各商品の販売回数合計を計算
total_counts <- colSums(df_wide[product_names])
# 各商品の購入頻度表を作成
result <- product_names |>
map_dfr(~ { # purrr::map_dfr()を使ってデータフレームを結合
df_wide |>
filter(!!sym(.x) == 1) |> # !!sym()で変数名を展開
select(-レシート番号) |>
summarise(
across(everything(), sum)
) |> # 商品ごとに合計
mutate(
across(everything(), ~ ifelse(cur_column() == .x, total_counts[.x], .)),
商品 = .x)
}) |>
select(商品, everything())
# ここから下は表の設定なので、なくても動作します
result |>
gt() |>
fmt_number(columns = 2:8, decimals = 0) |>
tab_options(
table.font.size = "normal",
heading.title.font.size = "normal",
) |>
gt_color_rows(2:8, palette = "ggsci::blue_material") |>
tab_header(title = "一緒に販売された商品の個数") |>
gt_theme_pff()| 一緒に販売された商品の個数 | |||||||
|---|---|---|---|---|---|---|---|
| 商品 | 緑茶 | 濃い茶 | おいしい緑茶 | おいしい濃茶 | 静岡の緑茶 | ほうじ茶 | ウーロン茶 |
| 緑茶 | 65,755 | 11,426 | 15,441 | 10,835 | 9,737 | 8,149 | 6,668 |
| 濃い茶 | 11,426 | 45,982 | 10,761 | 7,476 | 6,795 | 5,677 | 4,577 |
| おいしい緑茶 | 15,441 | 10,761 | 84,832 | 17,948 | 12,663 | 10,724 | 8,618 |
| おいしい濃茶 | 10,835 | 7,476 | 17,948 | 59,910 | 8,760 | 7,398 | 5,963 |
| 静岡の緑茶 | 9,737 | 6,795 | 12,663 | 8,760 | 46,516 | 5,691 | 4,622 |
| ほうじ茶 | 8,149 | 5,677 | 10,724 | 7,398 | 5,691 | 39,190 | 3,862 |
| ウーロン茶 | 6,668 | 4,577 | 8,618 | 5,963 | 4,622 | 3,862 | 31,905 |
各項目の値を合計値で割ることで、商品ごとの購入率を求めます。
result_ratio <- result |>
mutate(
緑茶 = 緑茶 / 緑茶[1],
濃い茶 = 濃い茶 / 濃い茶[2],
おいしい緑茶 = おいしい緑茶 / おいしい緑茶[3],
おいしい濃茶 = おいしい濃茶 / おいしい濃茶[4],
静岡の緑茶 = 静岡の緑茶 / 静岡の緑茶[5],
ほうじ茶 = ほうじ茶 / ほうじ茶[6],
ウーロン茶 = ウーロン茶 / ウーロン茶[7]
)
# ここから下は表の設定
result_ratio |>
gt() |>
fmt_number(columns = 2:8, decimals = 3) |>
tab_options(table.font.size = "small") |>
gt_color_rows(2:8, palette = "ggsci::blue_material") |>
tab_header(title = "一緒に販売された商品の割合(個数/縦合計)") |>
gt_theme_pff()Warning: Domain not specified, defaulting to observed range within each
specified column.| 一緒に販売された商品の割合(個数/縦合計) | |||||||
|---|---|---|---|---|---|---|---|
| 商品 | 緑茶 | 濃い茶 | おいしい緑茶 | おいしい濃茶 | 静岡の緑茶 | ほうじ茶 | ウーロン茶 |
| 緑茶 | 1.000 | 0.248 | 0.182 | 0.181 | 0.209 | 0.208 | 0.209 |
| 濃い茶 | 0.174 | 1.000 | 0.127 | 0.125 | 0.146 | 0.145 | 0.143 |
| おいしい緑茶 | 0.235 | 0.234 | 1.000 | 0.300 | 0.272 | 0.274 | 0.270 |
| おいしい濃茶 | 0.165 | 0.163 | 0.212 | 1.000 | 0.188 | 0.189 | 0.187 |
| 静岡の緑茶 | 0.148 | 0.148 | 0.149 | 0.146 | 1.000 | 0.145 | 0.145 |
| ほうじ茶 | 0.124 | 0.123 | 0.126 | 0.123 | 0.122 | 1.000 | 0.121 |
| ウーロン茶 | 0.101 | 0.100 | 0.102 | 0.100 | 0.099 | 0.099 | 1.000 |
次に、ある商品が購入された場合に、他の商品も購入されるかどうかを調べます。
5.3 アソシエーション分析
アソシエーション分析とはマーケティングで用いられる分析手法の1つで、POSデータや購買データから、商品の関連性やパターンを見つける分析手法です。 この手法を理解するためには,確率の知識が必要となるので,先に条件付確率の考え方を学びます。
5.3.1 条件付確率
事象 \(A\) が生起する確率を \(\Pr (A)\) ,事象 \(B\) が生起する確率を \(\Pr (B)\) とします。 事象 \(A\) と事象 \(B\) が同時に生起する確率を \(\Pr (A \cap B)\) で表し,これを同時確率といいます。 また、事象 \(B\) が生起したときの事象 \(A\) の生起確率を \(\Pr (A \mid B)\) と表します。これを条件付確率といい、次の式で表されます。
\[ \Pr(A \mid B) = \frac{\Pr(A \cap B)}{\Pr(B)} \]
図にすると次のようになります。
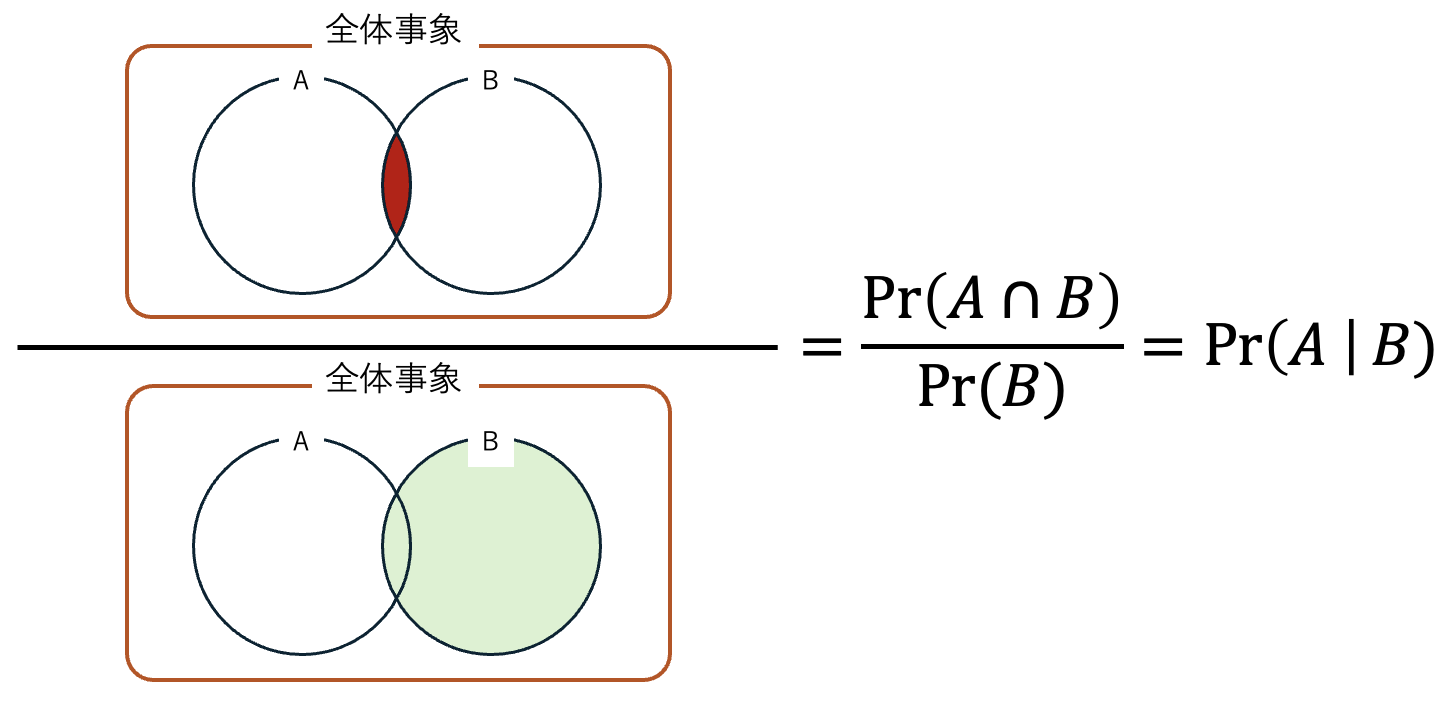
この式は次のように変形できます。 \[ \Pr(A \cap B) = \Pr(B) \times \Pr(A \mid B) \]
が成り立ちます。 これは事象 \(B\) が起こったときに事象 \(A\) が起こる確率 \(\Pr(A \mid B)\) に、事象 \(B\) が起こる確率 \(\Pr(B)\) を掛けることで、「事象 \(B\) が起こり、さらに事象 \(A\) が起こる確率」 \(\Pr(A \cap B)\) を求めることができるということです。 ここで \(\Pr(A)\) と \(\Pr(B)\) が独立である場合,\(\Pr(A \mid B) = \Pr(A)\) が成り立つため,\(\Pr(A \cap B) = \Pr(A) \times \Pr(B)\) となります。 \(\Pr(A)\) と \(\Pr(B)\) が独立でない場合,\(\Pr(A \mid B) \not = \Pr(A)\) となり,\(\Pr(A \cap B) \not = \Pr(A) \times \Pr(B)\) となります。
また \(\Pr(A) >0\) のときには、\(\Pr(A \cap B) = \Pr(A) \times \Pr(B \mid A)\) が成り立ちます。
5.3.2 アソシエーション分析の考え方
次に,商品の購買データを使ったアソシエーション分析について説明します。 いま,商品 \(A\) と商品 \(B\) がお店で販売されているとします。 ある商品 \(A\) が売れる確率を \(\Pr (A)\) で表し、商品 \(B\) が売れる確率を \(\Pr (B)\) で表します。
\(\Pr (B) \not = 0\) のとき、\(B\) が売れたときの商品 \(A\) の売れる確率を条件付確率 \(\Pr (A \mid B)\) で表します。 ここで,\(\Pr (A \cap B)\) は商品 \(A\) と商品 \(B\) が同時に売れる確率を表し,\(\Pr (B)\) は条件なしで商品 \(B\) が売れる確率を表します。 つまり,条件付確率とは,無条件で商品 \(B\) が売れた場合に,商品 \(A\) が同時に売れる確率を求めるものです。
ここでは \(\Pr (A)\) は確率というよりも,特定の商品の販売個数を全商品の販売個数で割った割合で,頻度を示しています。 条件付確率 \(\Pr (A \mid B)\) ある特定の商品が売れた場合に限定して,その他の商品が売れる確率を求めるものです。
商品 \(B\) を買った人が同時に商品 \(A\) も買う条件付確率 \(\Pr(A \mid B)\) が、条件なしで商品 \(A\) を買う確率 \(\Pr (A)\) よりも高いなら,
\[ \frac{\Pr (A \mid B)}{\Pr (A)} > 1 \]
となります。 条件付確率の定義を使うと、この式の左辺は次のように変形できます。 \[ \begin{aligned} \frac{\Pr (A \mid B)}{\Pr (A)} &= \Pr(A \mid B) \times \frac{1}{\Pr (A)} \\ &= \frac{\Pr (A \cap B)}{\Pr (B)} \times \frac{1}{\Pr (A)} \\ &= \underbrace{\frac{\Pr (A \cap B)}{\Pr (B) \Pr (A)}}_{\text{リフト値}} \gtreqqless 1 \end{aligned} \]
これをリフト値(Lift)といい,つぎように解釈します。
- リフト値が1を超えているとき、商品 \(A\) を買う確率よりも商品 \(B\) を買った場合に商品 \(A\) も買う確率のほうが高い。
- リフト値が1のときは,商品 \(A\) の購買確率と商品 \(B\) の購買確率が独立である,つまり無関係であることを意味します。
- リフト値が1未満のときは,商品 \(B\) が売れたとき,商品 \(A\) が通常より売れない,つまり負の相関があることを意味します。
図にすると次のようになります。
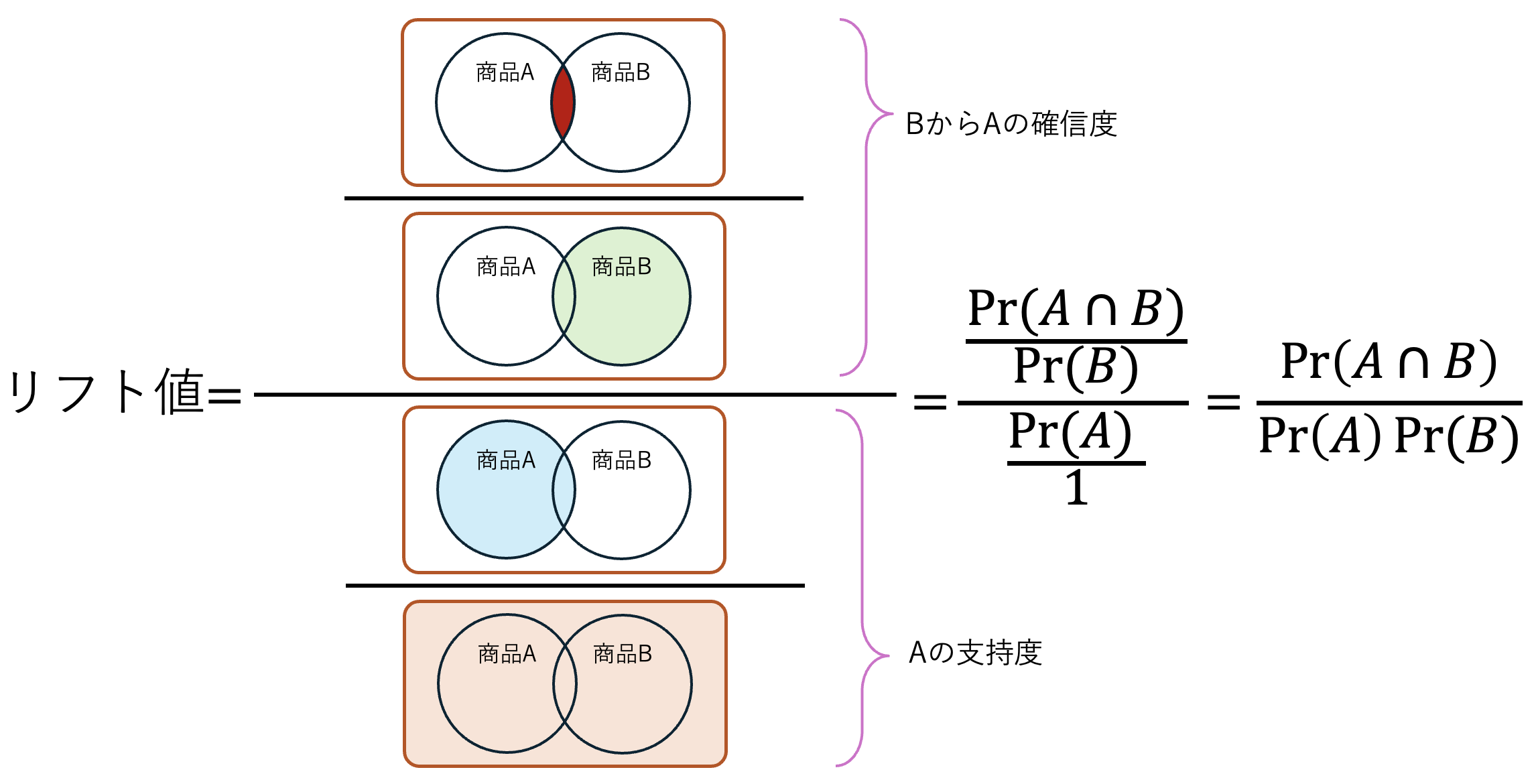
要するに,リフト値は商品 \(B\) が売れたとき商品 \(A\) が発生する確率が、単に商品 \(B\) とは無関係に \(A\) が販売される確率と比較してどれだけ高いかを示します。 このようにリフト値から二つの事象が同時に起こる可能性の高さを分析する方法をアソシエーション分析(Association Analysis)といいます。
5.3.3 支持度と確信度
また、このリフト値の分子 \(\Pr(A \cap B)\) は商品 \(A\) と商品 \(B\) が同時に売れる確率であり、これをアソシエーション分析ではAとBの支持度(support)と呼びます。 図にすると,次のようになります。
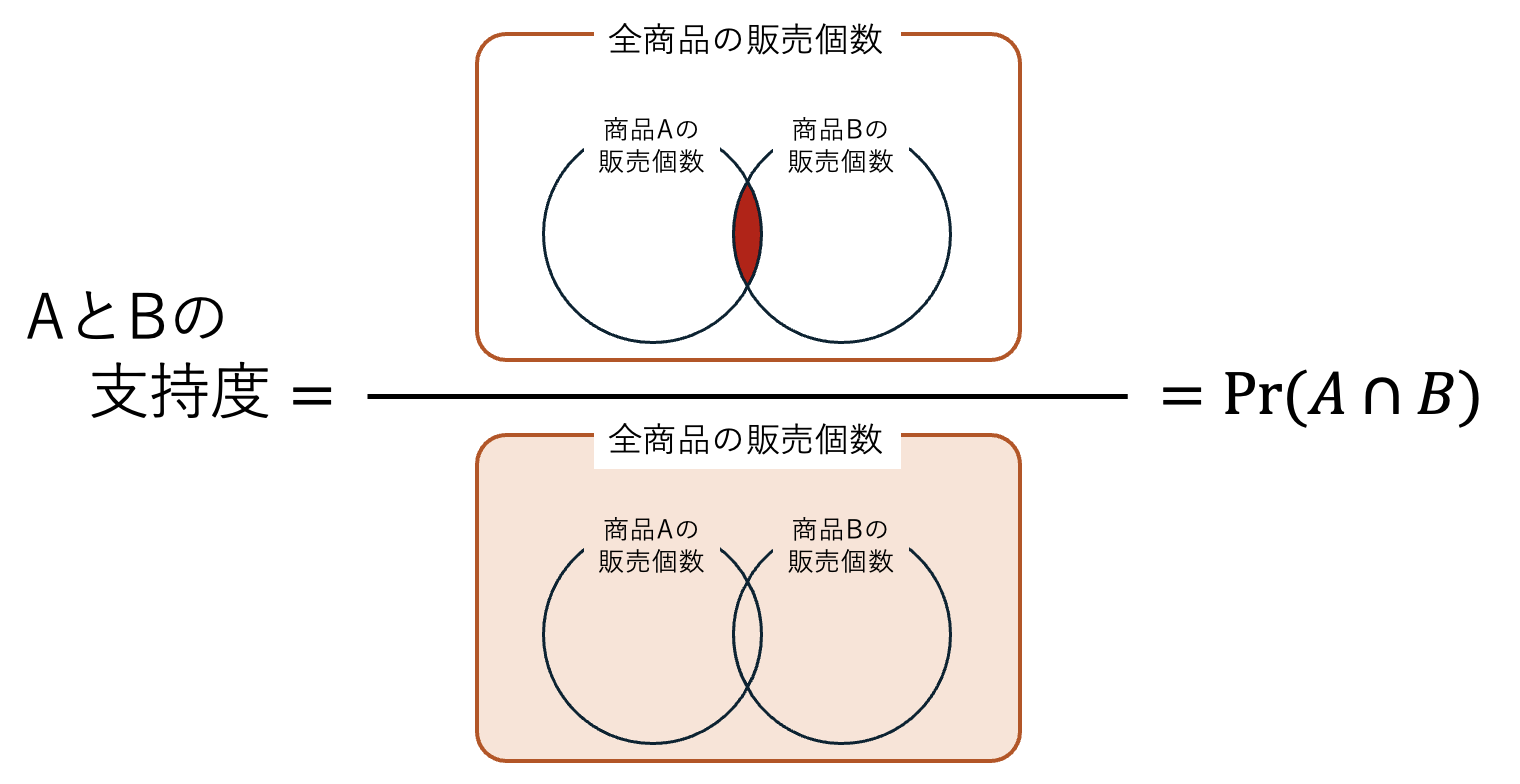
要するに,全ての購買のうち,AとBが同時に売れたケースの出現頻度を測る指標です。
また、\(B\) を買った人のうち \(A\) も買った人の割合を表す条件付確率 \(\Pr(A \mid B)\) を確信度(\(B \rightarrow A\))(confidence)と呼びます。
信頼度ということもあります。
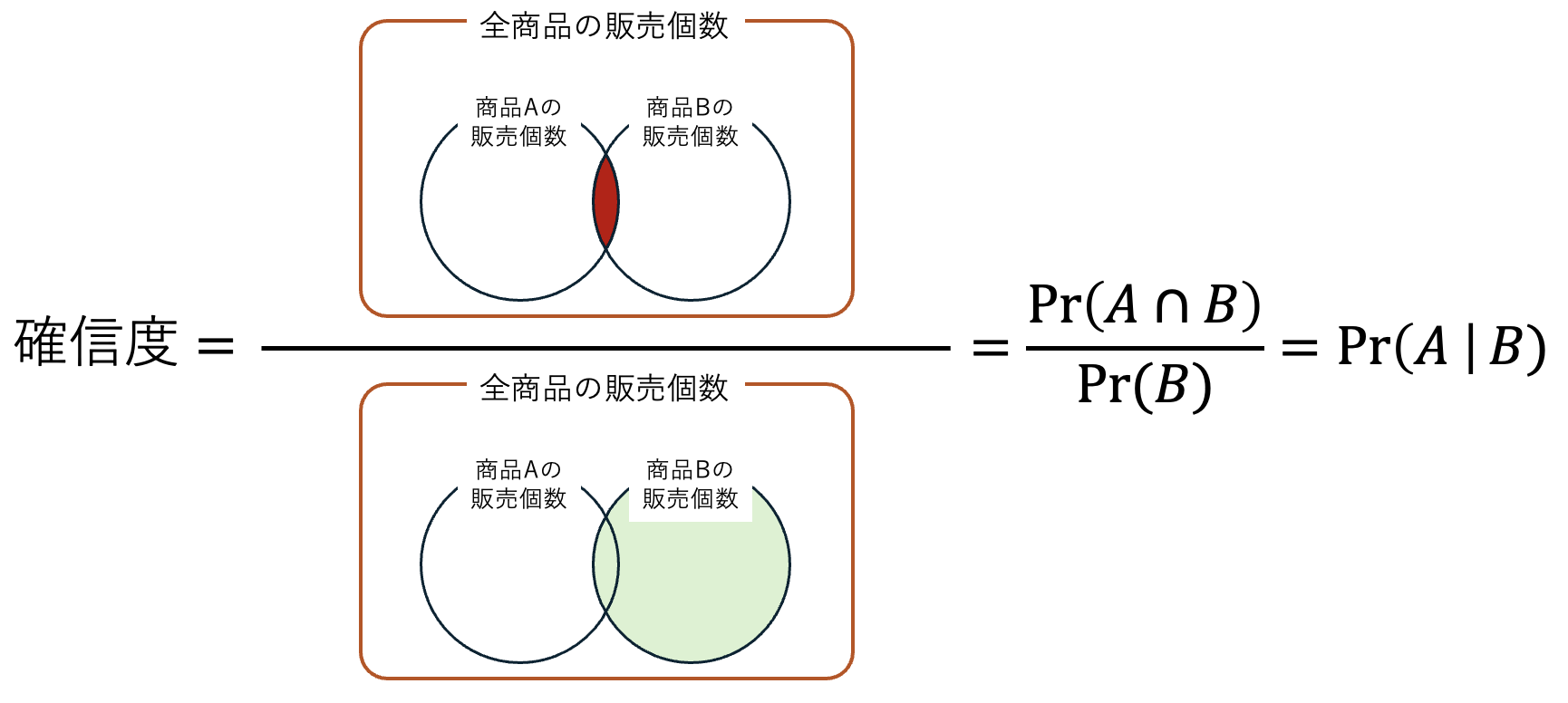
\(B\) が売れた場合に,\(A\) も売れるという状況がどれだけ確実に予測できるかを示します。 条件付確率 \(\Pr (A \mid B)\) が高いということは,\(B\) が売れたときは \(A\) も高い確率で売れる,ということを意味します。
5.4 Rでアソシエーション分析
アソシエーション分析のために用いるデータとして7番目のシート「併売データ」を読み込みたいので,sheet = 7を指定します。
df_associ <- readxl::read_excel("data/chp5.xlsx", sheet = 7)
head(df_associ)| お茶 | 炭酸飲料 | 弁当類 | パン類 | お菓子 | アイス |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 |
列は商品名で、各セルには購入された場合に1、購入されなかった場合に0が入っている観測値1000のデータフレームが読み込まれました。
5.4.1 arulesパッケージ
Rでアソシエーション分析を行うために,arulesパッケージを使います。 CRANのページにあるマニュアルにMining Association Rules and Frequent Itemsetsとあるように、関連ルールと頻出アイテムセットを見つけるためのパッケージです。
具体的な理論とアルゴリズムは,CRANのVignettes:introduction to arulesを参照してください。
ここで用いるarulesパッケージのapriori()関数は、関連ルールに関する制限を識別し、Klemettinen (1994)のアプリオリアルゴリズムを実装しています。
アソシエーション分析を行うために、まずはデータをtransactionsオブジェクトに変換します。 arules::as()関数を使って変換します。この関数は引数としてlistやmatrixを受け取り、transactionsオブジェクトに変換します。
順番に処理していきます。 df_associはread_excel()関数で読み込んだため、data.frame型となっています。 これをas.matrix()で行列型に変換し、その後as()関数でtransactionsオブジェクトに変換し、df_tranに代入します。
df_tran <- df_associ |>
as.matrix() |> # 行列型に変換
as("transactions") # transactionsオブジェクトに変換次に、apriori()関数を使ってアソシエーション分析を行います。 この関数は、transactionsオブジェクトを引数として受け取り、parameter引数でサポートと信頼度を指定します。 ここでは、サポートを0.05、信頼度を0.4とし、結果をdf_apに代入します。
df_apには、アソシエーション分析の結果が格納されているので、sort()関数を使ってliftでソートし、inspect()関数で結果を表示します。
result <- df_ap |>
sort(by = "lift") |> # liftでソート
inspect() # 結果を表示 lhs rhs support confidence coverage lift
[1] {炭酸飲料, 弁当類} => {お茶} 0.138 0.8214286 0.168 1.2834821
[2] {炭酸飲料, アイス} => {お茶} 0.058 0.7435897 0.078 1.1618590
[3] {お茶, アイス} => {炭酸飲料} 0.058 0.5800000 0.100 1.1284047
[4] {お茶, お菓子} => {炭酸飲料} 0.056 0.5773196 0.097 1.1231899
[5] {弁当類} => {お茶} 0.283 0.7128463 0.397 1.1138224
[6] {お茶} => {弁当類} 0.283 0.4421875 0.640 1.1138224
[7] {炭酸飲料} => {お茶} 0.358 0.6964981 0.514 1.0882782
[8] {お茶} => {炭酸飲料} 0.358 0.5593750 0.640 1.0882782
[9] {} => {炭酸飲料} 0.514 0.5140000 1.000 1.0000000
[10] {} => {お茶} 0.640 0.6400000 1.000 1.0000000
[11] {炭酸飲料, お菓子} => {お茶} 0.056 0.6292135 0.089 0.9831461
[12] {お茶, 弁当類} => {炭酸飲料} 0.138 0.4876325 0.283 0.9487014
[13] {お茶, パン類} => {炭酸飲料} 0.052 0.4814815 0.108 0.9367344
[14] {炭酸飲料, パン類} => {お茶} 0.052 0.5909091 0.088 0.9232955
[15] {お菓子} => {炭酸飲料} 0.089 0.4708995 0.189 0.9161468
[16] {アイス} => {お茶} 0.100 0.5813953 0.172 0.9084302
[17] {アイス} => {炭酸飲料} 0.078 0.4534884 0.172 0.8822731
[18] {弁当類} => {炭酸飲料} 0.168 0.4231738 0.397 0.8232953
[19] {お菓子} => {お茶} 0.097 0.5132275 0.189 0.8019180
[20] {パン類} => {お茶} 0.108 0.4886878 0.221 0.7635747
count
[1] 138
[2] 58
[3] 58
[4] 56
[5] 283
[6] 283
[7] 358
[8] 358
[9] 514
[10] 640
[11] 56
[12] 138
[13] 52
[14] 52
[15] 89
[16] 100
[17] 78
[18] 168
[19] 97
[20] 108 結果が見づらいので、arules::apriori()関数の結果をdata.frame型に変換し、変数名を補い、gt()関数で表形式にします。
result <- result |>
as.data.frame() # data.frame型に変換
names(result)[2] <- "arrow" # 変数名を補う
result |>
gt() |> # 表形式にする
fmt_number(columns = 4:7, decimals = 2) |>
tab_options(
table.font.size = "small"
)| lhs | arrow | rhs | support | confidence | coverage | lift | count |
|---|---|---|---|---|---|---|---|
| {炭酸飲料, 弁当類} | => | {お茶} | 0.14 | 0.82 | 0.17 | 1.28 | 138 |
| {炭酸飲料, アイス} | => | {お茶} | 0.06 | 0.74 | 0.08 | 1.16 | 58 |
| {お茶, アイス} | => | {炭酸飲料} | 0.06 | 0.58 | 0.10 | 1.13 | 58 |
| {お茶, お菓子} | => | {炭酸飲料} | 0.06 | 0.58 | 0.10 | 1.12 | 56 |
| {弁当類} | => | {お茶} | 0.28 | 0.71 | 0.40 | 1.11 | 283 |
| {お茶} | => | {弁当類} | 0.28 | 0.44 | 0.64 | 1.11 | 283 |
| {炭酸飲料} | => | {お茶} | 0.36 | 0.70 | 0.51 | 1.09 | 358 |
| {お茶} | => | {炭酸飲料} | 0.36 | 0.56 | 0.64 | 1.09 | 358 |
| {} | => | {炭酸飲料} | 0.51 | 0.51 | 1.00 | 1.00 | 514 |
| {} | => | {お茶} | 0.64 | 0.64 | 1.00 | 1.00 | 640 |
| {炭酸飲料, お菓子} | => | {お茶} | 0.06 | 0.63 | 0.09 | 0.98 | 56 |
| {お茶, 弁当類} | => | {炭酸飲料} | 0.14 | 0.49 | 0.28 | 0.95 | 138 |
| {お茶, パン類} | => | {炭酸飲料} | 0.05 | 0.48 | 0.11 | 0.94 | 52 |
| {炭酸飲料, パン類} | => | {お茶} | 0.05 | 0.59 | 0.09 | 0.92 | 52 |
| {お菓子} | => | {炭酸飲料} | 0.09 | 0.47 | 0.19 | 0.92 | 89 |
| {アイス} | => | {お茶} | 0.10 | 0.58 | 0.17 | 0.91 | 100 |
| {アイス} | => | {炭酸飲料} | 0.08 | 0.45 | 0.17 | 0.88 | 78 |
| {弁当類} | => | {炭酸飲料} | 0.17 | 0.42 | 0.40 | 0.82 | 168 |
| {お菓子} | => | {お茶} | 0.10 | 0.51 | 0.19 | 0.80 | 97 |
| {パン類} | => | {お茶} | 0.11 | 0.49 | 0.22 | 0.76 | 108 |
5.4.2 併売データの基礎集計
次に併売データの基礎集計を行います。 商品ごとの購買回数を集計します。
| お茶 | 炭酸飲料 | 弁当類 | パン類 | お菓子 | アイス |
|---|---|---|---|---|---|
| 640 | 514 | 397 | 221 | 189 | 172 |
1度に何種類の商品を購入するかを集計します。
同時に2種類の商品を購入するケースが最も多いようです。 どの商品との組み合わせが多いのかを、商品の組ごとの購買回数を調べます。
prod_name <- colnames(df_associ)
prod_pair <- combn(prod_name, 2, simplify = FALSE)
prod_counts <- sapply(prod_pair, function(pair) {
sum(df_associ[[pair[1]]] & df_associ[[pair[2]]])
})
result <- data.frame(
商品ペア = sapply(prod_pair, paste, collapse = " & "),
購入回数 = prod_counts
) |>
arrange(desc(購入回数))
result| 商品ペア | 購入回数 |
|---|---|
| お茶 & 炭酸飲料 | 358 |
| お茶 & 弁当類 | 283 |
| 炭酸飲料 & 弁当類 | 168 |
| お茶 & パン類 | 108 |
| お茶 & アイス | 100 |
| お茶 & お菓子 | 97 |
| 炭酸飲料 & お菓子 | 89 |
| 炭酸飲料 & パン類 | 88 |
| 炭酸飲料 & アイス | 78 |
| 弁当類 & パン類 | 73 |
| 弁当類 & お菓子 | 67 |
| 弁当類 & アイス | 57 |
| パン類 & お菓子 | 43 |
| パン類 & アイス | 32 |
| お菓子 & アイス | 28 |